suivant: 2.4 Bilan d'énergie monter: 2. Lois de bilan précédent: 2.2 Bilan de la Table des matières
Pour un écoulement stationnaire, l'équation de bilan locale de quantité
de mouvement s'écrit sous forme conservative (en notant
![]() le tenseur identité ):
le tenseur identité ):
Pour un écoulement stationnaire, le flux de quantité
de mouvement et de pression
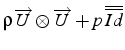 est nul à travers n'importe quelle surface fermée (théorème de la
divergence)
est nul à travers n'importe quelle surface fermée (théorème de la
divergence)
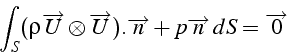
De façon générale, si la surface de contrôle contient une section
d'entrée ![]() , une section de sortie
, une section de sortie ![]() , et des frontières
non débitantes
, et des frontières
non débitantes ![]() (parois solides), les équations précédentes
s'écrivent:
(parois solides), les équations précédentes
s'écrivent:
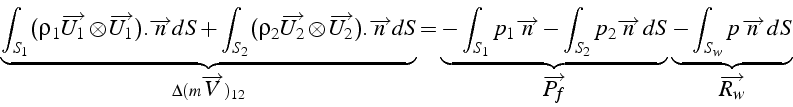
qui traduisent le théorème fondamental de la dynamique appliqué au volume de contrôle fluide:
“la variation de la quantité
de mouvement dans le volume fluide ( i.e la différence de flux entre
l'entrée et la sortie
![]() ) est égale
à la somme des forces extérieures appliquées au volume fluide ( i.e.
la force exercée par le fluide extérieur
) est égale
à la somme des forces extérieures appliquées au volume fluide ( i.e.
la force exercée par le fluide extérieur
![]() et la force exercée par les parois
et la force exercée par les parois
![]() )”.
)”.
Cette relation se généralise au cas où d'autres forces s'exercent sur le fluide comme la gravité, en général négligeable, les forces électromagnétiques et même les frottements (que l'on a négligé ici).
En considérant le cas du domaine de la figure 2.1 pour un
écoulement bidimensionnel, on écrit la projection de ces équations
suivant ![]() et
et ![]() (en tenant compte de l'orientation des normales):
(en tenant compte de l'orientation des normales):
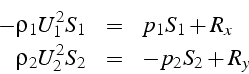
Donc dans l'exemple choisi la force
![]() exercée
par les parois sur le fluide a donc une composante
exercée
par les parois sur le fluide a donc une composante ![]() suivant
suivant
![]() négative et une composante
négative et une composante ![]() suivant
suivant ![]() positive (et
évidemment l'inverse pour la force exercée par le fluide sur les parois).
positive (et
évidemment l'inverse pour la force exercée par le fluide sur les parois).