2.2 Bilan de la masse

Pour un écoulement stationnaire, le bilan local de masse s'écrit:

$$div(\rho\overrightarrow{U})=0$$

Pour un écoulement stationnaire, le flux de masse est donc nul à travers n'importe quelle surface fermée (théorème de la divergence)

$$\int_{S}\rho\overrightarrow{U}.\overrightarrow{n}\, dS=0$$

Figure 2.1: volume de contrôle

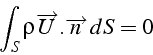
Considérons par exemple, le cas du domaine ci-dessus 2.1 avec une entrée $S_{1}$ et une sortie $S_{2}$ , et des frontières non débitantes $S_{W}$ (parois solides où $\overrightarrow{U}.\overrightarrow{n}=0$). Le bilan de masse s'écrit:

$$\int_{\Gamma}\rho\overrightarrow{U}.\overrightarrow{n}\, dS=... ...{S_{2}}\rho_{2}\overrightarrow{U_{2}}.\overrightarrow{n}\, dS=0$$

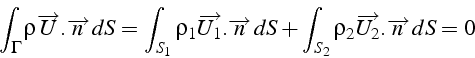
puisque l'intégrale sur $S_{W}$ est nulle.

En supposant $\rho$ et $\overrightarrow{U}$ constants dans chaque section (valeurs moyennes), et $U_{1}$ et $U_{2}$ les vitesses débitantes (i.e. normales à la section) suivant les axes, l'équation de bilan de masse s'écrit:

$$-\rho_{1}U_{1}S_{1}+\rho_{2}U_{2}S_{2}=0$$

Dans le cas d'un fluide incompressible $(\rho=cste)$, on retrouve l'équation de conservation du débit