2.1 Bilan sur un volume de contrôle

Nous avons vu que les équations d'Euler régissant l'écoulement adiabatique non visqueux d'un fluide parfait s'écrit sous la forme

$$\frac{\partial W_{i}}{\partial t}+div(\overrightarrow{F_{i}}(\overrightarrow{W}))=0$$

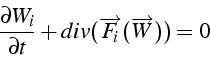
où $\overrightarrow{W}=\left[\begin{array}{ccccc} \rho & \rho u & \rho v & \rho w & \rho(e+\frac{1}{2}U^{2})\end{array}\right]$ est le vecteur d'état, et $F_{i}(\overrightarrow{W})$ le vecteur flux associé:

$$\overrightarrow{F}_{\rho}=\left[\begin{array}{c} \rho u\\ \... ...{c} \rho uh_{t}\\ \rho vh_{t}\\ \rho wh_{t}\end{array}\right]$$

où on a noté $e_{t}=e+\frac{1}{2}U^{2}$ l'énergie totale par unité de masse, et $h_{t}=e+\frac{p}{\rho}+\frac{1}{2}U^{2}$ l'enthalpie totale par unité de masse.

Pour un écoulement stationnaire, les variables d'état $W$ sont indépendantes du temps, et les équations d'Euler s'écrivent:

$$div(\overrightarrow{F_{i}}(\overrightarrow{W}))=0$$

Si on intègre ces équations dans un volume quelconque de fluide $\Omega,$ de frontière $\Gamma=\partial\Omega$ (figure ci-dessous), en utilisant le théorème de la divergence, on obtient:

$$\int_{\Gamma}\overrightarrow{F_{i}}(\overrightarrow{W}).\overrightarrow{n}\, ds\,=0$$

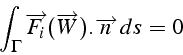
c'est à dire que les flux $\overrightarrow{F}_{i}(\overrightarrow{W})$ du vecteur d'état $\overrightarrow{W}$ se conservent, i.e. leurs intégrales à travers n'importe quelle surface fermée sont nulles.

Les variables d'état $\overrightarrow{W}$ sont appelées variables d'état conservatives. Ce ne sont pas les seules variables d'état permettant de décrire un fluide parfait: on peut faire d'autres choix, comme par exemple

$$\overrightarrow{W}=\left[\begin{array}{ccccc} \rho & u & v & w & p\end{array}\right]$$

que l'on appelle variables d'état physiques, mais dont les équations d'évolution ne s'écrivent pas sous forme conservative.