suivant: 1. Description d'un gaz monter: 0. Rappels précédent: 0.1 Rappel de Mathématique Table des matières
Un fluide, bien que constitué d'atomes au niveau microscopique, peut
être considéré au niveau macroscopique comme un milieu continu: c'est
à dire que les propriétés du fluide sont des fonctions continues des
variables d'espace ![]() et du temps
et du temps ![]() .
.
Décrire le mouvement d'un fluide fait appel à des notions différentes de celles développées en Mécanique du point ou du solide. Le fluide est en mouvement continue et on parle donc d'écoulement de fluide. Contrairement au solide, on s'intéresse donc plus à la vitesse des particules fluides qu'à leur déplacement ou déformation comme en mécanique des solides.
Pour décrire un fluide, on introduit la notion de “particule fluide”.
On isole (par la pensée ou en trouvant un moyen de visualisation,
coloration par exemple) des parties restreintes du fluide, appelée
“particules fluide”. Ces “particules fluides”
contiennent statistiquement le même nombre de molécules et doivent
avoir un volume ![]() dont la dimension
dont la dimension ![]() vérifie les hypothèses
de milieu continue:
vérifie les hypothèses
de milieu continue:
et dans un volume molaire ![]() :
:
il y a
![]() atomes d'hélium. Donc une particule
fluide de taille
atomes d'hélium. Donc une particule
fluide de taille
![]() , il y a
, il y a
![]() atomes.
atomes.
Pour une particule fluide, on peut alors définir:
On peut, de manière analogue à ce que l'on fait en Mécanique du solide, isoler (par la pensée ou en trouvant un moyen de visualisation, coloration par exemple) une partie restreinte du fluide appelée particule fluide et la "suivre" au cours du temps c'est à dire connaıtre à chaque instant sa position.
Soit ![]() la position de la particule à l'instant
la position de la particule à l'instant ![]() , de coordonnées
, de coordonnées
![]() , la vitesse de la particule aura
pour composantes:
, la vitesse de la particule aura
pour composantes:
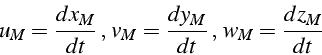
Au cours du temps, la particule sera en différents points M , l'ensemble des points M constitue la trajectoire de la particule. Cette façon de faire est appelée méthode de Lagrange, les variables introduites sont appelées variables de Lagrange. Elle s'avère dans la plupart des cas délicate car il n'est pas facile de suivre toutes les particules et elle est peu employée.
Cette méthode d'Euler consiste à connaıtre la vitesse des particules
au cours du temps t à un endroit donné déterminé par ses coordonnées,
par exemple cartésiennes ![]() . Elle est plus employée que la
méthode de Lagrange, la connaissance du champ des vitesses étant suffisante
pour la description du fluide en mouvement.
. Elle est plus employée que la
méthode de Lagrange, la connaissance du champ des vitesses étant suffisante
pour la description du fluide en mouvement.
On choisit un petit élément de volume ![]() , dont la position
, dont la position
![]() est fixe dans le référentiel de l'observateur, et on détermine
la vitesse des particules fluides qui traversent cet élément de volume.
La vitesse
est fixe dans le référentiel de l'observateur, et on détermine
la vitesse des particules fluides qui traversent cet élément de volume.
La vitesse
![]() mesurée dépend évidemment du temps
mesurée dépend évidemment du temps
![]() et du point de mesure
et du point de mesure ![]() :
:
De façon générale, les propriétés du fluide mesurées par la méthode
d'Euler dépendent donc du point ![]() et du temps
et du temps ![]() .
.
Si l'on compare les fluides avec les solides, la première remarque qui s'impose concerne l'isotropie (les propriétés sont les mêmes dans toutes les directions spatiales) des fluides usuels qui est toujours réalisée (si l'on agit pas sur le fluide en tout cas!).
En particulier, en un point quelconque d'un fluide, la pression est indépendante de la direction de la normale à la surface élémentaire sur laquelle elle s'exerce (théorème de Pascal).
L'écoulement du fluide est permanent ou stationnaire si ses composantes de vitesse sont indépendantes de la variable temps t ; il est dit non-permanent ou instationnaire si cette condition n'est pas réalisée.
L'écoulement du fluide est uniforme si ses composantes de vitesse sont indépendantes des coordonnées d'espace; il est non-uniforme si cette condition n'est pas remplie.
On appelle ligne de courant , à un instant t fixé, une courbe
dont la direction tangente en chacun de ses points est la direction
du vecteur vitesse. L'équation d'une ligne de courant se calcule par
intégration, à un instant t fixé, des équations suivantes (en notant
![]() la tangente en
la tangente en ![]() à la ligne de courant):
à la ligne de courant):
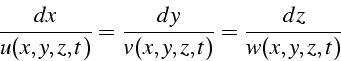
Si la vitesse n'a pas de composante suivant ![]() , l'écoulement est
plan ou bi-dimensionnel. Les particules fluides restent dans le plan,
et la vitesse ne dépend en général que de
, l'écoulement est
plan ou bi-dimensionnel. Les particules fluides restent dans le plan,
et la vitesse ne dépend en général que de ![]() et du temps
et du temps ![]() .
.
Si la vitesse a une seule composante de vitesse ![]() , l'écoulement
est 1D. Les trajectoires et les lignes de courant sont des droites.
, l'écoulement
est 1D. Les trajectoires et les lignes de courant sont des droites.
Considérons la fonction scalaire ![]() rendant compte d'une
grandeur physique caractéristique du fluide au point de coordonnées
rendant compte d'une
grandeur physique caractéristique du fluide au point de coordonnées
![]() et au temps t. La particule fluide au temps
et au temps t. La particule fluide au temps ![]() sera
au point de coordonnées
sera
au point de coordonnées
![]() . La
variation de la fonction
. La
variation de la fonction ![]() sera donc égale à :
sera donc égale à :
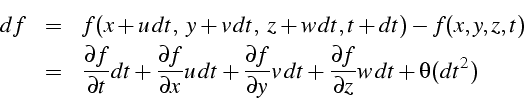
La dérivée ![]() , que l'on note
, que l'on note ![]() et que
l'on appelle dérivée particulaire, est égale à :
et que
l'on appelle dérivée particulaire, est égale à :
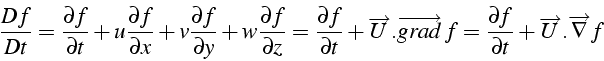
Au cours du mouvement, une particule de fluide subit des changements
de position, d'orientation et de forme. Nous considérons deux points
voisins ![]() ) et
) et
![]() d'un même fluide. Leurs
vitesses respectives
d'un même fluide. Leurs
vitesses respectives
![]() et
et
![]() s'écrivent à un instant
s'écrivent à un instant ![]() donné (en utilisant des développements
limités):
donné (en utilisant des développements
limités):
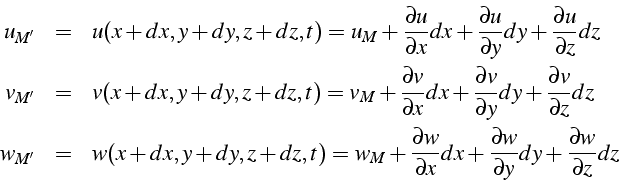
Ces expressions s'écrivent sous forme matricielle:
En décomposant la matrice des gradients de vitesse
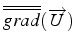 en sa partie symétrique et anti-symétrique, ces relations peuvent
se réécrire sous la forme suivante :
en sa partie symétrique et anti-symétrique, ces relations peuvent
se réécrire sous la forme suivante :

soit sous forme vectorielle
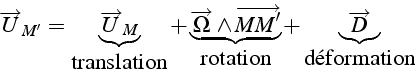
D'une manière générale, le mouvement d'une particule fluide est la superposition d'une translation, d'une rotation et d'une déformation.
![\includegraphics[width=0.8\textwidth]{cinematique}](img143.png)
Animation de la trajectoire (à gauche) et de la déformation seule (à droite) d'une particule fluide initialement carrée dans un champ de vitesse compressible
(Rem: noté le changement de surface de la particule)

