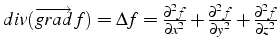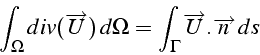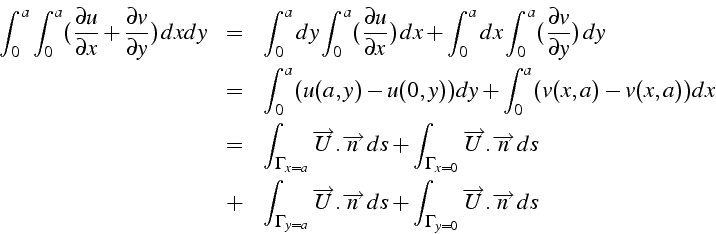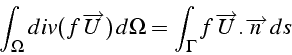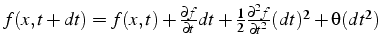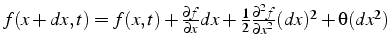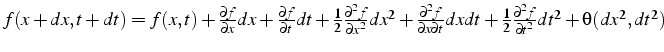Sous-sections
Soient
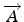 et
et
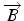 deux vecteurs
de
deux vecteurs
de 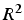 :
:
- composantes dans un repère cartésien :
![$[A_{1},A_{2}]$](img23.png) ou
ou
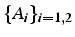 ,
,
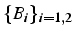
- produit scalaire: scalaire
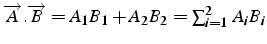
- norme euclidienne:
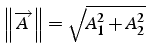
- produit vectoriel: vecteur
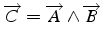 perpendiculaire au plan d'amplitude
perpendiculaire au plan d'amplitude
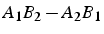
- produit tensoriel: matrice
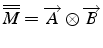 =
=
![$\left[\begin{array}{cc}
A_{1}B_{1} & A_{1}B_{2}\\
A_{2}B_{1} & A_{2}B_{2}\end{array}\right]$](img31.png) avec
avec
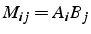
- on note
![$\left[x_{1},x_{2}\right]$](img33.png) les coordonnées cartésiennes d'un
point dans le repère
les coordonnées cartésiennes d'un
point dans le repère
![$[\overrightarrow{e_{1}},\overrightarrow{e_{2}}]$](img34.png) ,
ou
,
ou
![$\left[x,y\right]$](img35.png) dans le repère
dans le repère
![$[\overrightarrow{e_{x}},\overrightarrow{e_{y}}]$](img36.png)
Soient
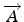 et
et
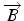 deux vecteurs
de
deux vecteurs
de 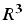 :
:
- composantes dans un repère cartésien :
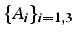 ,
,
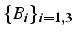
- produit scalaire: scalaire
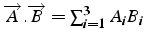
- produit vectoriel: vecteur
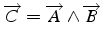 avec
avec
![$\overrightarrow{C}=\left[\begin{array}{ccc}
A_{2}B_{3}-A_{3}B_{2}, & A_{3}B_{1}-A_{1}B_{3}, & A_{1}B_{2}-A_{2}B_{1}\end{array}\right]$](img41.png)
- produit tensoriel: matrice
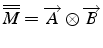 avec
avec
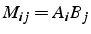
- on note
![$\left[x_{1},x_{2},x_{3}\right]$](img42.png) les coordonnées cartésiennes
d'un point dans le repère
les coordonnées cartésiennes
d'un point dans le repère
![$[\overrightarrow{e_{1}},\overrightarrow{e_{2}},\overrightarrow{e_{3}}]$](img43.png) ,
ou
,
ou
![$\left[x,y,z\right]$](img44.png) dans le repère
dans le repère
![$[\overrightarrow{e_{x}},\overrightarrow{e_{y}},\overrightarrow{e_{z}}]$](img45.png)
- exemple:
-
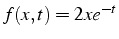
- dérivée partielle en temps:
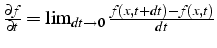
- dérivée partielle en espace:
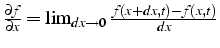
- sa différentielle est un scalaire:
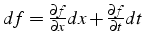
- exemple:
-
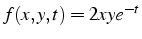
- sa différentielle est un scalaire:
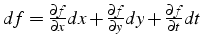
- son gradient (par rapport aux variables spatiales) est un vecteur
de composantes
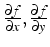
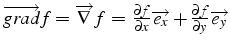
A un instant t fixé, c'est un vecteur perpendiculaire aux courbes
iso-valeurs 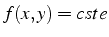 , qui indique la direction où la fonction
, qui indique la direction où la fonction
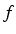 croıt.
croıt.
- on note
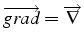 le vecteur
opérateur dérivé:
le vecteur
opérateur dérivé:
![$\overrightarrow{\nabla}=\left[\begin{array}{ccc}
\frac{\partial}{\partial x} & ...
...c{\partial}{\partial x_{1}} & \frac{\partial}{\partial x_{2}}\end{array}\right]$](img57.png)
- exemple:
-
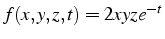
- sa différentielle est un scalaire:
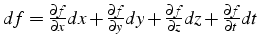
- son gradient (par rapport aux variables spatiales) est un vecteur:
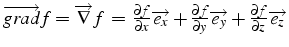
c'est une fonction vectorielle de composantes
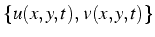
- exemple:
-
![$\overrightarrow{U}(x,y,t)=\left[\begin{array}{cc}
2xye^{-t} & (x^{2}+y^{2})e^{t}\end{array}\right]$](img62.png)
- sa matrice Jacobienne est la matrice des gradients:
- sa divergence est un scalaire:
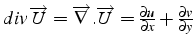 .C'est la trace de
.C'est la trace de 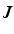 .
.
Elle traduit la compression ou l'expansion du champs
- son rotationnel est un vecteur perpendiculaire au plan d'amplitude:
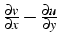
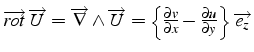
Il traduit la rotation solide du champ
- l'opérateur scalaire
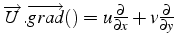
traduit le transport par le champ d'une quantité:
donne un scalaire appliqué à un scalaire:
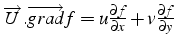
et un vecteur appliqué à un vecteur:
c'est une fonction vectorielle de composantes
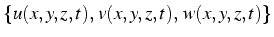
- sa divergence est un scalaire:
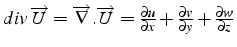
- son rotationnel est un vecteur:
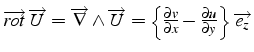
- l'opérateur scalaire
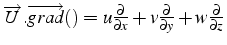
donne un scalaire appliqué à un scalaire:
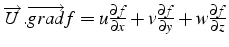
et un vecteur appliqué à un vecteur:
Notons enfin quelques propriétés de ces opérateurs:
- On généralise facilement au cas du flux
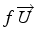 d'un
scalaire
d'un
scalaire 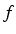
- développement limité en temps
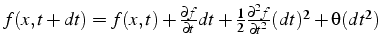
- développement limité en espace
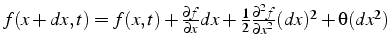
- développement limité en temps et en espace:
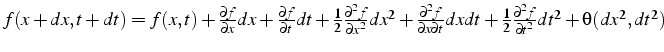
Pr. Marc BUFFAT
marc.buffat@univ-lyon1.fr
2007-03-06
![]() et
et
![]() deux vecteurs
de
deux vecteurs
de ![]() :
:
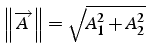
![$\left[\begin{array}{cc}
A_{1}B_{1} & A_{1}B_{2}\\
A_{2}B_{1} & A_{2}B_{2}\end{array}\right]$](img31.png) avec
avec
![]() et
et
![]() deux vecteurs
de
deux vecteurs
de ![]() :
:
![$\overrightarrow{\nabla}=\left[\begin{array}{ccc}
\frac{\partial}{\partial x} & ...
...c{\partial}{\partial x_{1}} & \frac{\partial}{\partial x_{2}}\end{array}\right]$](img57.png)
![]()
![\begin{displaymath}
J=\left[\begin{array}{cc}
\frac{\partial u}{\partial x} & \f...
...rray}\right]=\left[\frac{\partial u_{i}}{\partial x_{j}}\right]\end{displaymath}](img63.png)
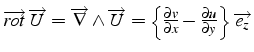
![\begin{displaymath}
\overrightarrow{U}.\overrightarrow{grad}\overrightarrow{U}=\...
...v}{\partial x}+v\frac{\partial v}{\partial y}\end{array}\right]\end{displaymath}](img71.png)
![]()
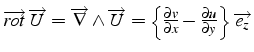
![\begin{displaymath}
\overrightarrow{U}.\overrightarrow{grad}\overrightarrow{U}=\...
...w}{\partial y}+w\frac{\partial w}{\partial z}\end{array}\right]\end{displaymath}](img76.png)