M2 Image
TP2 - plus de cubes...
Partie 1 : des cubes
maintenant que vous savez afficher des objets, comment peut on
dessiner un ensemble de cubes pour représenter une scène façon
Minecraft ? par exemple :

l'idée est d'utiliser une carte d'altitude / un terrain pour
positionner quelques milliers de cubes. par exemple, en
utilisant cette image (cf repertoire data/terrain) :

exercice 1 :
placer les cubes et dessinez-les directement avec les
utilitaires de gKit
rappel : la camera
regarde l'axe -Z
exercice 2 :
même question, utilisez un shader et dessinez directement
avec glDrawArrays() / glDrawElements(), cf la
doc...
si nécessaire
exercice 3 : le bon
draw !
même question, existe-t-il un draw openGL plus adapté à ce type
d'affichage ? (ie dessiner plein de fois le même cube)
comment l'utiliser ? qui ira plus vite ? le cpu ? le gpu ? les 2
?
Partie 2 : des cubes différents
on souhaite enrichir un peu plus la scène en utilisant des cubes
différents, en fonction de l'altitude, par exemple :

vous pouvez utiliser le pack
d'objets de
quaternius :
cube_world.zip
(ou un autre, au choix)
exercice 1 :
c'est malin, comment peut-on dessiner rapidement une scène
composée d'objets différents ?
bonus : et avec des
personnages / animaux qui se promènent dans la scène ? et de la
végétation ?
Partie 3 : trop de cubes
lorsque la scène devient trop grande, dessiner tous les cubes
qui ne sont pas visibles dans l'image devient très / trop long.
une idée est de découper la carte en régions, et de vérifier
qu'une région est visible par la camera (ie dans son frustum)
avant de la dessiner.
exercice 1 :
comment déterminer qu'un point est visible par la camera ? ie
qu'il appartient à son frustum ?
exercice 2 :
même question pour un cube aligné sur les axes ? comment
déterminer que le cube est, au moins en partie, visible ?
serait-il plus simple de vérifier que le cube n'est pas visible
?
proposez un test qui vérifie qu'un cube ne peut pas etre
visible. l'idée est de trouver un plan qui sépare le frustum et
le cube...
indication : c'est la
même idée que pour dessiner un triangle, si tous les sommets
d'un objet sont de l'autre coté du plan, les 2 objets sont
séparés...
indication : le frustum
est un cube aligné sur les axes dans le repère projectif...
exercice 3 :
utilisez le test précédent et ne dessinez que les régions
visibles.
euh, c'est malin, comment on fait pour continuer à utiliser
l'instanciation ?
indication : et si on
changeait le contenu du buffer d'instances ? ie celui qui
contient les positions des cubes à dessiner...
quelle taille choisir pour une région ? quelle influence peut
avoir ce parametre ?
Partie 4 : et les ombres ?
lorsque l'on dessine un triangle, on a pas d'information sur les
autres triangles qui pourraient lui faire de l'ombre...
il va falloir dessiner 2 fois la scène,
- une fois pour le point de vue de la source de lumière, et
- une autre fois, comme d'habitude, pour le point de vue de la
camera.
mais on "garde" les triangles visibles par la source de lumière,
on sait qu'ils sont éclairés, c'est le résultat de la 1ere étape.
pour chaque pixel de l'image dessinée pour le point de vue de la
source on connait la distance entre la source de lumière et le
triangle visible.
ensuite, lorsque l'on dessine la scène pour le point de vue de la
camera, on transforme le point visible pour la camera dans le
repère / le point de vue de la source. il ne reste plus qu'à
comparer la distance entre le point transformé et la source avec
la distance de la 1ere étape, qui correspond au triangle le plus
proche de la source, ie celui qui est éclairé. si le point est à
la bonne distance / sur le triangle éclairé, il est lui aussi
éclairé, sinon sa distance est plus grande et il est à l'ombre.
exercice 1 : dessinez la scène pour le point de vue de la
source de lumière.
on commence par construire les transformations qui permettent
d'observer la scène depuis la position de la source de lumière. il
faut, comme d'habitude, définir les transformations model, view,
projection et image.
le plus direct est d'utiliser une projection ortographique, cf Ortho()
qui "projette" un cube [left .. right] x [bottom .. top] x
[znear .. zfar] du repère camera vers le repère
projectif.
des exemples complets sont dans la doc en ligne, cf "decals
et projection de textures"
exercice 2 : création du framebuffer et des textures
étape suivante, il faut conserver les triangles visibles par la
source de lumière, ils seront éclairés. ces triangles sont aussi
les plus proches de la source de lumière (par construction), on
veut conserver au minimum le zbuffer, ie la distance entre la
source de lumière et le triangle visible / éclairé.
la création / configuration d'un framebuffer est assez directe,
mais il y a bien sur quelques détails techniques à régler, cf "rendu
multi-passes". vous pouvez utiliser les utilitaires de texture.h
pour créer simplement les textures nécessaires, cf
make_depth_texture() ou make_vec3_texture(), etc. elles sont
faites exactement pour ça !
au final, votre code ressemblera à :
GLuint shadow_map=
make_depth_texture( /* unit */ 0, /* width */ 256, /* height */
256 );
GLuint framebuffer= 0;
glGenFramebuffers(1,
&framebuffer);
glBindFramebuffer(GL_DRAW_FRAMEBUFFER, framebuffer);
glFramebufferTexture(GL_DRAW_FRAMEBUFFER, /* attachment */
GL_DEPTH_ATTACHMENT, shadow_map, /* mipmap */ 0);
// verification de la
configuration du framebuffer
if(glCheckFramebufferStatus(GL_DRAW_FRAMEBUFFER) !=
GL_FRAMEBUFFER_COMPLETE)
return
"error";
// nettoyage...
glBindFramebuffer(GL_DRAW_FRAMEBUFFER, 0);
pour dessiner dans le framebuffer, il ne reste plus qu'à le
sélectionner (avant de dessiner la scene), mais attention aux
paramètres implicites du draw() !
(par exemple les dimensions de l'image... cf glViewport())
exercice 3 : et maintenant les ombres !!
et voila, tout est pret !! il ne reste plus qu'à dessiner la
scène depuis le point de vue de la camera et à écrire le test qui
vérifie qu'un point (vu par la camera) est plus près ou plus loin
que le triangle éclairé par la source de lumière. les détails de
la projection et des transformations sont dans "decals
et projection de textures" / section "finir le calcul :
projetter le décal"
attention : dans le shader, la fonction texture(shadow_map,
uv) renvoie un vec4, la distance stockée dans la texture
se trouve dans la composante .x ou .r (et pas .z qui sera
toujours 0...)
exercice 4 : et maintenant ? des ombres propres !!
et voila ça marche !

ou pas, c'est quand même moche, non ?
argh, mais pourquoi ??
le zbuffer stocke une distance par pixel lorsque l'on dessine un
triangle pour le point de vue de la source de lumière :
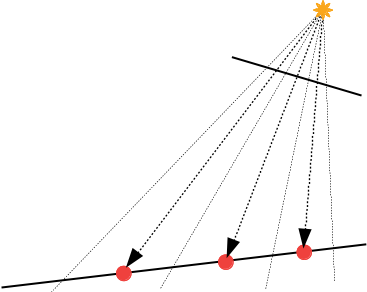
ie la distance entre le point rouge et la source. mais lorsque l'on
dessine le même triangle depuis la camera / un autre point de vue :
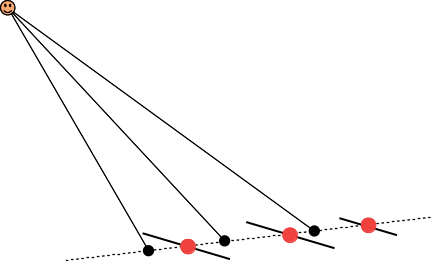
les centres des fragment de l'image se projettent sur des point
différents à la surface du triangle. et comparer la distance des
points rouges et des points noirs à la source de lumière est assez
approximatif, ce qui crée tous les defauts des ombres dans l'image
précédente.
bien sur, il y a plusieurs solutions : on peut ajouter une
tolérance lors de la comparaison (comme pour le lancer de rayon,
cf
doc
en ligne), on peut arrondir la position du point pour
correspondre au point stocké, et recalculer sa distance avant de
faire la comparaison, on peut aussi stocker (ou recalculer) la
normale du triangle et interpoler la distance, etc. mais le test
reste quand même fragile. on peut aussi stocker l'indice du
triangle, dessiner les faces arrieres au lieu des faces avant (en
modifiant les parametres du test d'orientation des triangles),
etc. mais ces tests ne sont pas plus simples ni plus robustes.
on peut aussi remarquer que le test est faux puisque l'on compare
les distances de 2 points differents alors qu'il assez simple de
faire un test plus robuste (en faisant un peu plus de calculs...)
l'idée est relativement simple : on connait le point p (visible
depuis la camera, en noir), et il faut calculer le point sur le
même triangle que p qui se projette sur le centre du texel, en
rouge. c'est un calcul d'intersection entre le plan du triangle
et le rayon entre la source de lumiere et le centre du pixel du
zbuffer sur lequel se projette p. cf
principes
du lancer de rayon / intersection rayon / plan pour les
détails du calcul. au final, le plus "compliqué" est d'obtenir
les coordonnées des points et vecteurs dans le même repère pour
faire les calculs d'intersection.
pourquoi ça marcherait mieux que les autres
tests ? par construction chaque pixel du zbuffer / shadow map
conserve la distance entre le point visible pour le centre du
fragment et la source de lumière / centre de la projection
utilisée pour dessiner les triangles. lorsque l'on dessine les
mêmes triangles pour le point de vue de la camera, avec une
autre projection, le centre d'un fragment d'un triangle se
projette sur un autre point du triangle. et comme ce sont des
points différents, leurs distances à la source sont
différentes. cette solution recalcule le point du triangle
visible par le centre du fragment, ce qui permet de comparer
cette profondeur à celle stockée dans le zbuffer.
et ça marche ?












