on vient de voir dans synthèse réaliste et intégration numérique : l'équation de rendu que l'on a besoin d'estimer l'intégrale d'une fonction pour calculer la lumière réfléchie par un point de la scène. et qu'une méthode assez proche de l'intégration par rectangles n'est pas tout à fait adaptée au problème... mais qu'il existe une autre méthode : intégration numérique et Monte Carlo. par contre, les exemples précédents d'intégration avec Monte Carlo n'etaient qu'en une seule dimension. comment utiliser Monte Carlo pour intégrer l'équation de rendu ?
c'est à dire comment utiliser ça :
\[ \begin{eqnarray*} I &= &\int f(x)\, dx\\ I &\approx &\frac{1}{N} \sum_i^N \frac{f(x_i)}{p(x_i)} \end{eqnarray*} \]
pour calculer ça :
\[ L_r(p, \vec{o})= \int_{\Omega} \frac{k}{\pi} V(p, \vec{l}) L_i(p, \vec{l}) \cos \theta \, dl \]
la démarche est toujours la même, on part de l'intégration à calculer et on écrit l'estimateur :
\[ \begin{eqnarray*} L_r(p, \vec{o}) &= & \int_{\Omega} \frac{k}{\pi} V(p, \vec{l}) L_i(p, \vec{l}) \cos \theta \, dl\\ &\approx & \frac{1}{N} \sum_j^N \frac{k}{\pi} V(p, \vec{l_j}) L_i(p, \vec{l_j}) \cos \theta \frac{1}{p(\vec{l_j})} \end{eqnarray*} \]
mais on se retrouve avec le même problème : on vient de remplacer la variable de l'intégration par une variable aléatoire et il faut définir sa densité de proba \( p( \vec{l} ) \) et savoir générer des directions en fonction de cette densité...
sans rentrer dans les détails, l'idée est de changer de variable dans l'intégration sur l'hémisphère en utilisant les angles \( (\theta, \phi) \) pour décrire une direction sur \( \Omega \), ce qui permet de faire apparaitre les 2 angles qui représentent une direction \( \vec{l} \) :
\[ \begin{eqnarray*} & & \int_{\Omega} f(\vec{l}) \cos \theta \, dl\\ &= & \int_{0}^{2\pi}\int_{0}^{\pi/2} f\left( \vec{l}(\theta, \phi ) \right) \cos \theta \sin \theta \, d\theta \, d\phi \end{eqnarray*} \]
ensuite, il faut construire les 2 densités de proba, celles de \( \theta \) et \( \phi \), puis leurs fonctions de répartition et enfin les inverser pour générer une direction en utilisant 2 nombres aléatoires uniformes \( u_1, u_2 \) compris entre 0 et 1. un exemple plus simple (en 1d) est présenté dans intégration numérique et Monte Carlo section "générer des points avec une densité de proba continue..."
par exemple, on peut construire une direction uniforme \( \vec{v} \) sur \( \Omega \) avec :
\[ \begin{eqnarray*} p(\vec{v})&= & \frac{1}{2\pi}\\ \cos \theta &= & u_1\\ \phi &= & 2\pi \, u_2\\ \vec{v} &= & ( \cos \phi \sin \theta, \, \sin \phi \sin \theta, \, \cos \theta)\\ \mbox{avec }\sin \theta &= & \sqrt{1 - \cos \theta \cos \theta} \end{eqnarray*} \]
et voila, on peut calculer une image maintenant, avec \( N = 64 \) par exemple :
 |  |
(à gauche l'intégration Monte Carlo, à droite l'intégration avec une spirale de Fibonacci)
mais ce n'est pas très différent de ce que l'on peut obtenir avec une spirale de Fibonacci orientée différemment pour chaque pixel... alors pourquoi ?
quel est l'intérêt d'avoir fait tout ça ?
de la même manière que l'on a re-écrit l'équation de rendu sur les angles \( (\theta, \phi) \) pour générer des directions sur l'hemisphère, on va pouvoir écrire une transformation différente qui permet de "viser" directement les sources de lumières et de placer tous les points au bon endroit... au lieu d'espérer trouver des sources de lumières en choisissant aléatoirement des directions. c'est à dire au lieu d'intégrer ces fonctions :
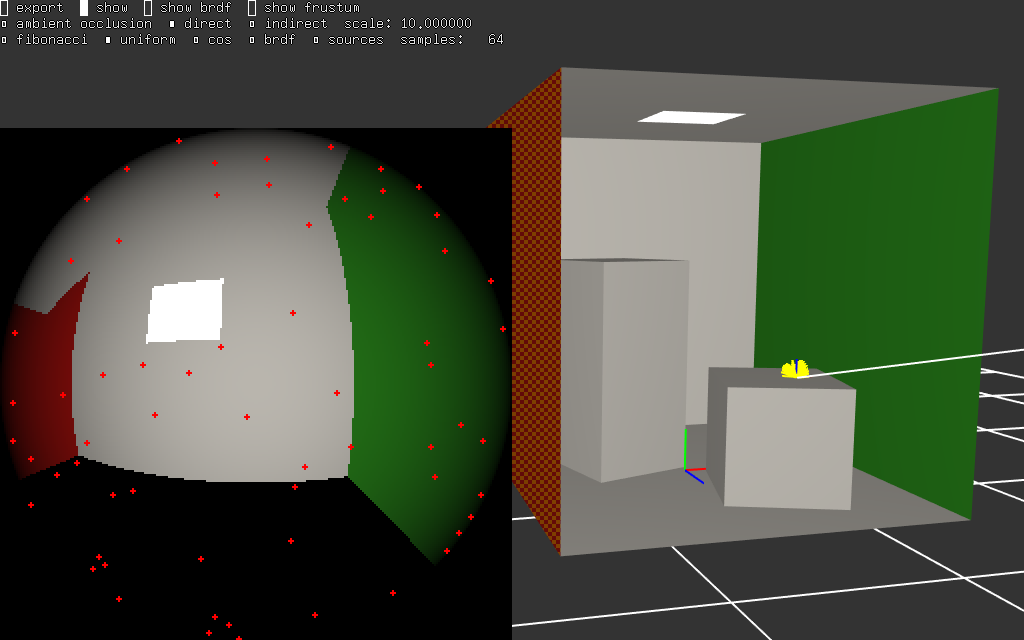 | 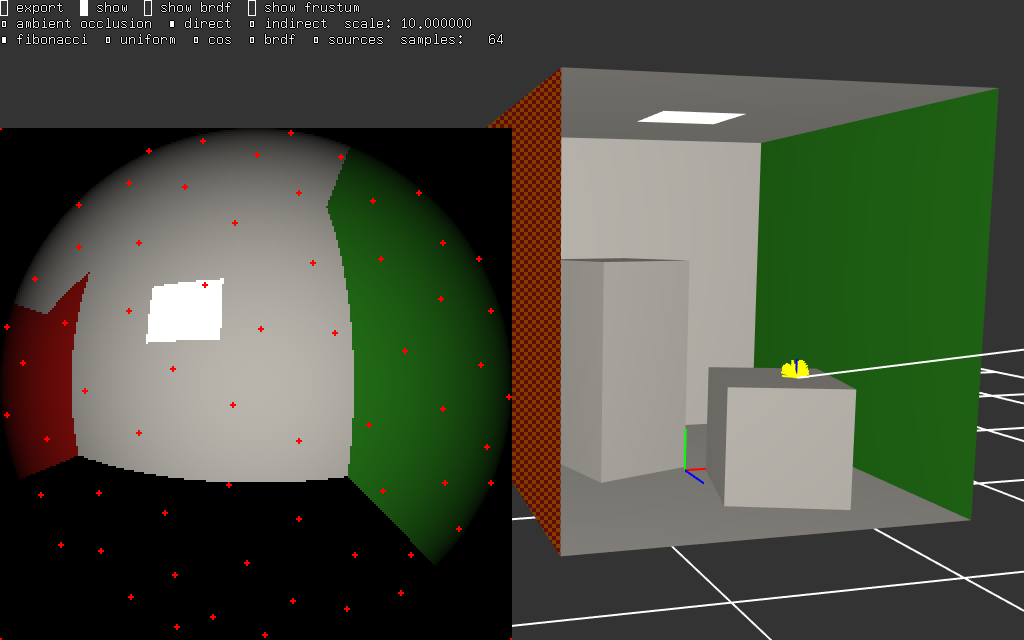 |
(c'est la même visualisation que dans synthèse réaliste et intégration numérique : l'équation de rendu, les sources de lumière sont en blanc dans la vignette en bas à gauche, les autres objets ne sont dessinés que pour rendre la vignette plus lisible)
on va directement viser les sources de lumière :
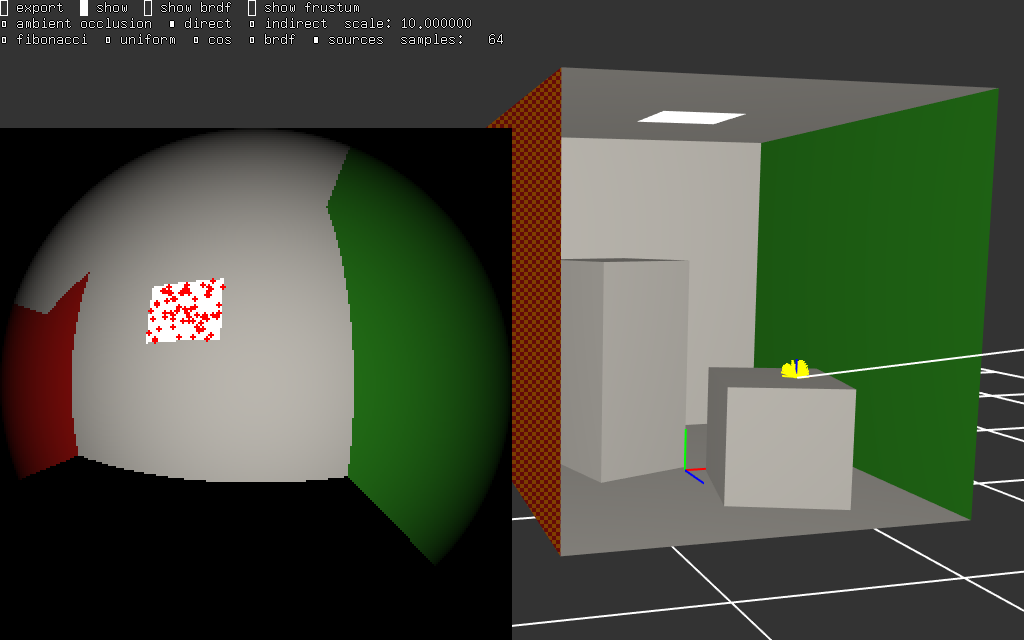
reformuler le problème...
le point de départ est le même :
\[ L_r(p, \vec{o})= L_e(p, \vec{o}) + \int_{\Omega} \frac{k}{\pi} V(p, \vec{l}) L_i(p, \vec{l}) \cos \theta \, dl \]
mais on va changer de variable d'intégration, pour écrire la même chose, en intégrant sur les points à la surface des objets :
\[ L_r(p, o)= L_e(p, o) + \int_{A} \frac{k}{\pi} V(p, q) L_i(p, q) \cos \theta_p \frac{\cos \theta_q}{||\vec{pq}||^2} \, dq \]
avec \( A \) l'aire de la surface des objets de la scène et le point \( q \) la nouvelle variable d'intégration. le changement de variable introduit également un terme supplémentaire, qui est nécessaire pour garantir que l'on calcule toujours la même chose, quelquesoit la forme de l'intégrale, soit sur des directions, soit sur des points...
pour les curieux : pourquoi \( dl= \sin \theta d\theta d\phi \) et pourquoi \( dl= \frac{\cos \theta_q}{||\vec{pq}||^2} dq\) ? un peu de lecture dans PBRT chapitre 5 : Working with Radiometric Integrals.
et alors ? connaissant un point \( q \) et sa matière, on peut maintenant utiliser le fait que certains points émettent de la lumière mais pas les autres... si \( q \) n'est pas sur une source, on sait que \( L_i(p, q) = 0 \), ie le point \( p \) ne récoit pas de lumière de \( q \). en pratique, on vient de séparer les points de la scène, ie le domaine d'intégration \( A \), en 2 parties : les points sur les sources \( S \) et les autres, \( A - S \). on peut écrire explicitement cette propriété :
\[ \begin{eqnarray*} L_r(p, o) &= & L_e(p, o) \\ &+ & \left[ \int_{A - S} \frac{k}{\pi} V(p, q) L_i(p, q) \cos \theta_p \frac{\cos \theta_q}{||\vec{pq}||^2} \, dq \right] = 0 \\ &+ & \int_{S} \frac{k}{\pi} V(p, q) L_i(p, q) \cos \theta_p \frac{\cos \theta_q}{||\vec{pq}||^2} \, dq\\ \end{eqnarray*} \]
et comme \( L_i(p, q) = 0 \) pour tous les points \( q \) qui ne sont pas sur les sources, toute cette partie du domaine d'intégration est nulle et ne contribue pas au résultat, il n'y a pas de raison de passer du temps à intégrer numériquement un résultat que l'on connait à l'avance (et qui est 0 en plus...)
ok, c'est peut etre interressant... mais il faut encore finir le calcul et pouvoir générer des points \( q \) aléatoirement sur les sources de lumière...
on commence par écrire l'estimateur Monte Carlo avec la densité de proba de la variable \( q \) :
\[ \begin{eqnarray*} L_r(p, o) &= & L_e(p, o) + \int_{S} \frac{k}{\pi} V(p, q) L_i(p, q) \cos \theta_p \frac{\cos \theta_q}{||\vec{pq}||^2} \, dq\\ &\approx & L_e(p, o) + \frac{1}{N} \sum_j^N \frac{k}{\pi} V(p, q_j) L_i(p, q_j) \cos \theta_p \frac{\cos \theta_{q_j}}{||\vec{pq_j}||^2} \, \frac{1}{p(q_j)} \end{eqnarray*} \]
on va commencer par un cas simple : on suppose qu'il n'y a qu'une source de lumière et que c'est un carré. quelle densité de proba peut-on utiliser ? par exemple, une densité uniforme, ie \( p(q)= \frac{1}{aire} \). on va utiliser 2 variables aléatoires, une pour choisir une position dans la longueur du carré, et une autre pour la hauteur, on utilise 2 fois le choix d'un point dans un intervalle (cf intégration numérique et Monte Carlo), la densité de q est le produit des 2 : \( p(q) = \frac{1}{largeur}\frac{1}{hauteur} = \frac{1}{aire}\)
si on connait un point \( a \) et les 2 arètes qui définissent la source, on peut écrire directement :
et ça marche ?
pour \( N = 4, 16 \) :
 |  |
c'est un poil mieux non ? pour comparer, les résultats précédents avec \( N = 64 \) ressemblaient à ça :
 |  |
même si les différentes étapes semblent bizarres et un peu compliquées, ie utiliser Monte Carlo, les densités de proba, leur inversion, la reformulation du problème, etc. on arrive à un résultat nettement plus convaincant qu'avec la première intégration numérique... et c'est aussi beaucoup plus rapide à calculer !!
bilan
pourquoi utiliser des trucs aussi compliqués pour calculer une image ? tout simplement parce que ce sont les bons outils pour formuler le problème, ie le calcul que l'on veut faire et estimer un résultat correct.
pourquoi une intégrale ? il faut demander aux physiciens / opticiens... mais le résultat n'est pas si surprenant lorsque l'on veut éclairer une scène avec autre chose qu'un point ou une direction...
et pourquoi Monte Carlo ? probablement parce que c'est la méthode la plus souple et la plus robuste pour calculer tout ça, même s'il est nécessaire de faire beaucoup de calculs, dans certains cas, pour obtenir une image propre et sans défauts. l'industrie n'utilise plus que cette solution pour produire les films d'animation et les effets spéciaux. par exemple :
- Hyperyon / Disney : "The Design and Evolution of Disney’s Hyperion Renderer",
- Renderman / Pixar : "RenderMan: An Advanced Path Tracing Architecture for Movie Rendering".
vous pouvez faire une soirée Toy story (par exemple) pour constater l'évolution de la qualité du rendu entre 1995 (Toy story 1) et 2010 (Toy Story 3) qui sont produits avec les méthodes classiques (ie le pipeline REYES) et comparer aux solutions plus récentes : 2019 (Toy Story 4) et 2022 (Buzz Lightyear) qui utilisent du lancer de rayons et de l'intégration Monte Carlo (ainsi que des modèles de matières réalistes de plus en plus détaillés)...
un peu de lecture sur les méthodes précédentes :
- REYES : un pipeline de fragmentation / rasterization, à peine plus général que celui utilisé par une carte graphique moderne,
cf "the Reyes image rendering architecture", Pixar, 1987, - approximation de l'éclairage global : cf "Coherent Out-of-Core Point-Based Global Illumination", Dreamworks, 2011.