monter: 3. Memo Matlab précédent: 3.18 Application: vibration d'une Table des matières
Pour analyser la réponse en fréquence d'un système mécanique régis par un ensemble d'équations différentielles à coefficients constant, on a recours à la transformation de Laplace.
La transformée de Laplace permet de transformer les équations différentielles à coefficients constants en relations algébriques plus simples.
Pour cela on définit la transformée de Laplace d'une fonction du temps
![]() (définie pour
(définie pour ![]() ) comme étant la fonction
) comme étant la fonction ![]() de
la variable complexe
de
la variable complexe ![]() :
:
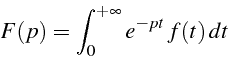
La transformation de Laplace vérifie en particulier la propriété suivante pour des conditions initiales nulles:
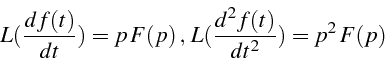
Considérons le système masse ressort amorti suivant (on note ![]() la masse,
la masse, ![]() la raideur et
la raideur et ![]() le coefficient d'amortissement)
se déplacant horizontalement sur un chariot:
le coefficient d'amortissement)
se déplacant horizontalement sur un chariot:
![\includegraphics[width=0.4\textwidth]{MECA/MRC}](img241.png)
On soumet ce système à une excitation ![]() et on veut
déterminer le déplacement
et on veut
déterminer le déplacement ![]() du système. Celui ci est solution
de l'équation différentielle du second ordre:
du système. Celui ci est solution
de l'équation différentielle du second ordre:
Par transformé de Laplace, on obtiens l'équation suivante:
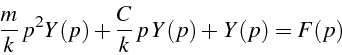
La fonction de transfert ![]() du système est le rapport de la sortie
du système est le rapport de la sortie
![]() sur l'entrée
sur l'entrée ![]() :
:
Pour une excitation harmonique
![]() , cette fonction
de transfert s'écrit (
, cette fonction
de transfert s'écrit (![]() :
:
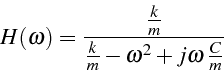
En notant
![]() la fréquence propre de résonnance
du système, et
la fréquence propre de résonnance
du système, et ![]() , la fonction de transfert s'écrit:
, la fonction de transfert s'écrit:
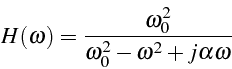
dont le module donne l'amplification en fréquence de la sortie par rapport à l'entrée:
Le tracé de cette fonction en échelle
![]() donne la
réponse en fréquence du système en régime permanent.
donne la
réponse en fréquence du système en régime permanent.
Le tracé en décibel (db=20![]() ) s'appelle le “diagramme
de Bode”. Un exemple de ces deux diagrammes est donnée
ci-dessous. On note bien sur ces diagrammes la résonnance pour la
fréquence propre
) s'appelle le “diagramme
de Bode”. Un exemple de ces deux diagrammes est donnée
ci-dessous. On note bien sur ces diagrammes la résonnance pour la
fréquence propre
![]() , la largueur du pic étant
fonction du paramêtre d'amortissement
, la largueur du pic étant
fonction du paramêtre d'amortissement ![]() . A haute fréquence
la pente en échelle log vaut
. A haute fréquence
la pente en échelle log vaut ![]() ou
ou ![]() en décibel. C'est
l'ordre du système différentiel (ici 2).
en décibel. C'est
l'ordre du système différentiel (ici 2).
![\includegraphics[width=0.5\textwidth]{MECA/freq}](img261.png)
![\includegraphics[width=0.5\textwidth]{MECA/bode}](img262.png)
L'équation différentiel 3.9 peut s'écrire comme un système
d'ordre 1 en introduisant le vecteur inconnu d'état
![$X=\left[\begin{array}{c}
y\\
\dot{y}\end{array}\right]$](img263.png) donnant la position
donnant la position ![]() et la vitesse
et la vitesse
![]() :
:
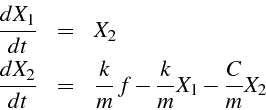
Ce système s'écrit sous forme matricielle
où
![$B=\left[\begin{array}{c}
0\\
k/m\end{array}\right]$](img268.png) est la matrice d'entrée
est la matrice d'entrée ![]() associée à l'entrée
associée à l'entrée ![]() , et
, et
![]() la matrice
la matrice
![\begin{displaymath}
A=\left[\begin{array}{cc}
0 & 1\\
-\frac{k}{m} & -\frac{C}{m}\end{array}\right]\end{displaymath}](img270.png)
La transformée de Laplace du système 3.12 s'écrit:
ce qui donne (en notant ![]() la matrice identitée 2x2) l'état
la matrice identitée 2x2) l'état
![]() en fonction de l'entrée
en fonction de l'entrée ![]()
La première composante de ce vecteur donne la fonction de transfert en position 3.10:
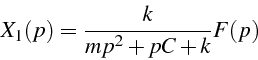
et la seconde la fonction de transfert en vitesse:
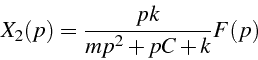
Le programme Matlab suivant 3.19.4 permet le tracé de la réponse
en fréquence de la fonction de transfert ![]()
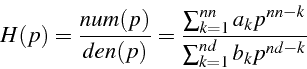
On fournit les coefficients
![]() et
et
![]() du polynôme en p du numérateur et du dénominateur (avec les conventions
Matlab pour les polynômes) ainsi que la gamme de fréquence
du polynôme en p du numérateur et du dénominateur (avec les conventions
Matlab pour les polynômes) ainsi que la gamme de fréquence
![]() .
.
function TraceBode(num,den,omega)
% trace du diagramme de Bode de la fonction de transfert
% H(p)=num(p)/den(p) avec p=i*omega
% Num et Den contiennent les coefficients reels
% des polynomes en p
% (C) M. BUFFAT 2005
nn=length(num); % degre numerateur
nd=length(den);
% calcul des coefficients complexes des polynomes en i*omega
NUM=zeros(nn,1);
for j=1:nn
NUM(j)=num(j)*(i)^(nn-j);
end;
DEN=zeros(nd,1);
for j=1:nd
DEN(j)=den(j)*(i)^(nd-j);
end;
% determination des valeurs
OMEGA=logspace(log10(omega(1)),log10(omega(2)),100);
% calcul du module
NH=abs(polyval(NUM,OMEGA))./abs(polyval(DEN,OMEGA));
% trace
loglog(OMEGA,NH,'LineWidth',2)
title('Reponse en Frequence');
xlabel('omega'); ylabel('|H|');
grid on
% fin
return
L'execution du programme 3.19.4 avec les parametres
![]() ,
,
![]() et pour
et pour ![]() :
:
>> TraceBode([100],[1,0.1,100],[1 1000])
fournit la courbe suivante:
![\includegraphics[width=0.8\textwidth]{MECA/TraceBode}](img284.png)