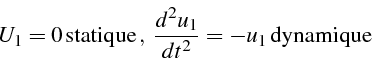suivant: 3.18 Application: vibration d'une monter: 3. Memo Matlab précédent: 3.16 Vibration d'un ressort Table des matières
Si on considère un système de ![]() “masse/ressort”, l'équilibre
statique est obtenu par résolution du système linéaire suivant:
“masse/ressort”, l'équilibre
statique est obtenu par résolution du système linéaire suivant:
où ![]() est la matrice de raideur (de dimension
est la matrice de raideur (de dimension ![]() ),
),
![]() le vecteur des déplacements aux noeuds (de dimension
le vecteur des déplacements aux noeuds (de dimension ![]() ) et
) et ![]() le vecteur des forces appliquées aux noeuds (de dimension
le vecteur des forces appliquées aux noeuds (de dimension ![]() ).
).
Si on écarte le système de sa position d'équilibre, il se met à osciller.
Le vecteur des déplacements aux noeuds ![]() dépend du temps
et est solution de :
dépend du temps
et est solution de :
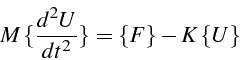
soit en introduisant le vecteur des oscillations ![]() autour de
la position d'équilibre statique:
autour de
la position d'équilibre statique:
C'est un système de ![]() équations différentielles linéaires du
second ordre. En se donnant l'amplitude du déplacement par rapport
à l'équilibre à l'instant initial (on lâche le système sans vitesse
initiale)
équations différentielles linéaires du
second ordre. En se donnant l'amplitude du déplacement par rapport
à l'équilibre à l'instant initial (on lâche le système sans vitesse
initiale)
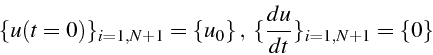
le système (3.7) admet alors une solution unique.
Cette solution est une combinaison linéaire des modes de vibrations propres, qui sont des solutions élémentaires de l'équation (3.7).
L'équation (3.7) peut se réécrire sous la forme:
où ![]() est une matrice symétrique définie positive3.1 .
est une matrice symétrique définie positive3.1 .
Cette matrice est donc diagonalisable et possède ![]() valeurs
propres positives
valeurs
propres positives
![]() . Chacune des valeurs
propres
. Chacune des valeurs
propres ![]() est associée à un vecteur propre
est associée à un vecteur propre ![]() ,
vérifiant:
,
vérifiant:
Une solution élémentaire de (3.8) s'écrit:
puisque :
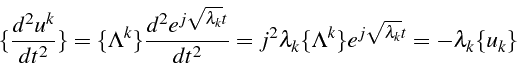
Ces solutions élémentaires sont indépendantes et forment une base de solutions de (3.8).
La solution générale de (3.8) est donc la combinaison linéaire de ces solutions élémentaires qui vérifie la condition initiale:
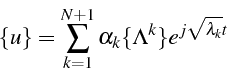
Ces solutions élémentaires ![]() sont les modes de vibrations propres
du système, associés aux fréquence propres
sont les modes de vibrations propres
du système, associés aux fréquence propres
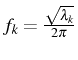 .
.