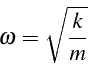suivant: 3.17 Vibrations libres d'un monter: 3. Memo Matlab précédent: 3.15 Application Table des matières
Considérons le ressort linéaire de raideur ![]() , dont l'extrémité
1 est fixe et ayant une masse
, dont l'extrémité
1 est fixe et ayant une masse ![]() accrochée à l'extrémité 2.
accrochée à l'extrémité 2.
![\includegraphics[width=0.6\textwidth]{MECA/ressort5}](img197.png)
L'équilibre statique du système soumis à une force extérieur ![]() s'écrit:
s'écrit:
Si on écarte la masse de cette position d'équilibre statique ![]() ,
le système oscille (vibration) avec un déplacement
,
le système oscille (vibration) avec un déplacement ![]() solution
de l'équation de la dynamique:
solution
de l'équation de la dynamique:
En décomposant le déplacement ![]() en déplacement statique
en déplacement statique
![]() et oscillation
et oscillation ![]() autour de cette position
d'équilibre:
autour de cette position
d'équilibre:
l'équation sur les vibrations libres ![]() s'écrit (relation
(3.6)-(3.5))
s'écrit (relation
(3.6)-(3.5))
Cette équation différentielle du second ordre admet une solution de la forme:
où ![]() est l'écart par rapport à l'équilibre à
est l'écart par rapport à l'équilibre à ![]() (on lâche le
système sans vitesse initiale) et
(on lâche le
système sans vitesse initiale) et ![]() est la pulsation libre
du système qui vaut:
est la pulsation libre
du système qui vaut: