3.14 Système masse ressort

Généralisons le modèle précédent en introduisant une masse en chacun des points, suivant le schéma ci dessous:

Ce système masse ressort peut modéliser la déformation élastique en traction/compression d'une poutre (solide de longueur >> à sa section droite $S$ ). En effet un élément de poutre homogène de longueur $l$ et de section $S$ constante, soumise à une force de traction $F$ en chacune de ses extrémités qui se déplacent d'une quantité $u_{1}$ et $u_{2}$, s'allonge (se déforme) d'une longueur $du=u_{2}-u_{1}$ proportionnelle à $F$ (dans la limite des petites déformations ou élasticité linéaire, la déformation est proportionnelle à la contrainte).

$$T=k\,(u_{2}-u_{1})$$

On peut donc modéliser cet élément de poutre par le système masse ressort suivant (on a répartit uniformément la masse de la poutre en chacune des extrémités):

La raideur du ressort $k$ dépend du coefficient d'élasticité du matériau $E$ (module d'Young), de la longueur $l$ et de la section $S$:

$$k=\frac{E\, S}{l}$$

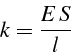
Pour de l'acier , $E\approx200\,10^{9}\, N/m^{2}$. Ainsi pour allonger de $1mm$ une tige d'acier de longueur $l=0.5m$, de diamètre $d=0.01m$, il faut appliquer une force de traction $F\approx31400\, N$ . La masse volumique de l'acier $\rho\approx8000\, kg/m^{3}$, et le poids de cette barre vaut donc $mg\approx6.28\, N$ .