Sous-sections
- Matlab
- langage de manipulation numérique de matrices
(voir aussi Scilab (http://www-rocq.inria.fr/scilab))
Matlab est une boite à outils d'analyse numérique, avec un environnement
agréable pour faire du calcul numérique avec sa programmation matricielle.
Il dispose des méthodes usuelles de l'analyse numérique:
- résolution de système linéaire
- détermination des valeurs propres
- résolution de problème non-linéaire
- résolution d'équations différentielles (raides)
- intégration numérique
- optimisation et contrôle
- graphique 2D et 3D
Utilisation de l'aide en ligne !!!
- clear
- efface toutes les variables
- variable
- définition lors de l'initialisation
- instruction
- si terminer par un
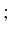 pas d'affichage du résultat
pas d'affichage du résultat
- vecteur ligne
- X=[1 2 3]; X=[1:0.5:3]; X=ones(1,5);
- vecteur colonne
- Y=[1;2;3]; Y=X'; Y=zeros(5,1);
- matrice
- A=[ 1 0; 0 1]; A=eye(2,2); M=[X;X]; M=[Y Y]; M=[Y;Y];M=A';
- opérations
- *, -, / , \ : X=A\B;
ou X=inv(A)*B;
- fonctions
- s'appliquent aux matrices
sin(A); A^2; A.^2;
sin(A).^2+cos(A).^2-ones(size(A))
- chaînes
- caractères entre 2 ' , concatenation S=['un'
' et deux'] (tableau de car.)
- entrée sortie
- disp(X); X=input('X=');
- for var=exp, inst., end
- boucle sur les colonnes de exp
- for var=1:n, inst, end
- boucle classique de 1 à n
Un premier exemple
X=rand(1,5);
S=0; for K=X, S=S+K^2, end;
qui peut s'écrire plus classiquement
X=rand(1,5);
S=0; for i=1:length(X), S=S+X(i)^2, end;
En général, on peut éviter les boucles explicites
- Exemple
- calcul d'un résidu partiel des lignes 2 à 4 d'un système
5*5
A=rand(5,5); X=rand(5,1); B=rand(5,1); R=zeros(5,1);
for i=2:4
R(i)=B(i)
for j=1:5
R(i)=R(i)-A(i,j)*X(j)
end
end
que l'on peut écrire plus efficacement
for i=2:4, R(i)=B(i)-A(i,1:5)*X(1:5), end
ou encore
R(2:4)=B(2:4)-A(2:4,1:5)*X(1:5);
- if cond , inst1 ,else inst2, end
- test classique (possibilité
de elseif)
if x<0, y=x, else, y=-x, end
- valeur logique:
- 0=faux, 1=vrai
- opérateurs logiques:
- & (et), | (ou), ~ (négation)
- opérateurs relationnels:
- <, <= ,> ,>= ,== ,~=
- fonctions logiques:
- any(Y==1), all(X==0)
- switch var, case val1, exp1; case val2, exp2; ...;otherwise, exp; end
-
switch num
case -1
disp('moins un');
case 1
disp('plus un');
case 0
disp('zero');
otherwise
disp('autres valeurs');
end
- while cond, inst., end
- exécute les instructions tant que la
cdt est vrai
n=1
while prod(1:n)<1.0e100
n=n+1
end
- continue
- passage à l'itération suivante
- break
- arrêt de la boucle interne
Un programme ou suite d'instructions Matlab peut être sauvegardé dans
un fichier script (M-File) ayant une extension .m
fichier program.m
- a=0; fa=-Inf;
- b=3; fb=-fa;
- while (b-a) >eps*b
- x=(a+b)/2; fx=x^3-2*x-5;
- if (sign(fx) == sign(fa))
- a=x; fa=fx;
- else
- b=x; fb=fx;
- end
- end
- x
Pour exécuter le script, il suffit de taper le nom du fichier sans
l'extension
>> program
Rem: les variables du script sont globales
Une fonction sont écrites dans un fichier avec une extension .m
(M-File) et le nom du fichier doit être le nom de la première fonction
définie (la seule visible). On l'exécute en tapant le nom avec des
arguments.
- fonction
- function arguments de sortie = nom(arguments d'entrée)
fonction racine
- function x=racine(a,b)
- % calcul la racine de la fonction f(x) définie ci-après sur [a,b]
- fa=f(a); fb=f(b); x=(a+b)/2;
- if (fa*fb>0) x=-Inf; return; end;
- while (b-a)>eps*x
- x=(a+b)/2; fx=f(x);
- if(sign(fx)==sign(fa))
- a=x; fa=fx;
- else
- b=x; fb=fx;
- end
- end
- % definition de f(x) (fonction locale)
- function y=f(x)
- y=x^3-2*x-5
Fonction calculant 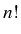
1ere version récursive
- function y=fact(n)
- if (n<=1) y=1
- else y=n*fact(n-1)
- end
2nd version avec une boucle
- function y=fact(n)
- y=1;
- for i=2:n, y=y*i, end
3ieme version optimisée
- function y=fact(n)
- y=prod(1:n);
- function handle
- pointeur vers une fonction=adresse
ptr_fonct=@fonction
- evaluation
- feval(ptr_fonct,liste arguments)
Calcul de l'intégrale
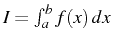 par la méthode des
trapézes
par la méthode des
trapézes
- function A=trapezes(ptr_f,a,b,n)
- h=(b-a)/n; X=[a:h:b]; Y=feval(ptr_f,X);
- A=h*((Y(1)+Y(n+1))/2+sum(Y(2:n)));
- % ou A=trapz(X,Y);
Utilisation
>> fp=@sin
>> A=trapezes(fp,0,pi)
Matlab est un langage matricielle!
il faut donc utiliser en priorité les notations matricielles
Exemple: calcul de la matrice de Vandermond 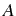
première version: méthode naturelle (identique au C)
- t=[0:1:200]; n=100;
- cpu0=cputime();
- m=size(t,1);
- for i=1:m
- for j=1:n+1
- A(i,j)=t(i)^(j-1);
- end
- end
- cputime()-cpu0
qui s'exécute en 4,87 sec
version matricielle optimisée
- cpu0=cputime();
- m=size(t,1);
- A=zeros(m,n+1);
- for i=1:n
- A(:,i+1)=A(:,i).*t;
- end
- cputime()-cpu0
Alors que la version matricielle s'exécute en 0,06 s, soit
80 fois plus rapidement
- E/S formattées
- générales et similaires au C
fid=fopen(nomfichier,permisson)
permission='r','w' (sous windows) 'rt','wt'
A=fscanf(fid,format)
format='%d %g %f %s %c'
count=fprintf(fid,format,A1,A2,..)
status=fclose(fid)
Pr. Marc BUFFAT
marc.buffat@univ-lyon1.fr
2008-01-29
![]()
![]()
![\begin{displaymath}
A^{t}=\left[\begin{array}{ccccc}
1 & t_{1} & t_{2} & .. & t_...
...\
1 & t_{1}^{m} & t_{2}^{m} & .. & t_{n}^{m}\end{array}\right]\end{displaymath}](img79.png)