4.1 Problème étudié

On considère une poutre en flexion de longueur L, encastrée en $x=0$ et soumise à une force de flexion $F$ en $x=L$.

On note $v(x)$ le déplacement transverse, $\rho$ la masse volumique , $S$ la section de la poutre, $E$ le module d'Young, $I_{zz}$ l'inertie de la section suivant z (perpendiculaire au plan). Avec l'hypothèse d'Euler Bernouilli (un plan normal à la ligne centrale reste normal à cette ligne après déformation), l'angle $\theta(x)$ de rotation du plan (suivant z) s'écrit:

$$\theta(x)=\frac{dv}{dx}$$

Dans une section, la résultante des contraintes est un torseur, qui comprend la résultante des contraintes de cisaillement $V_{y}=-EI_{zz}\frac{d^{3}v}{dx^{3}}$ et le moment fléchissant (moment des contraintes normales) $M_{z}=EI_{zz}\frac{d^{2}v}{dx^{2}}$ . L'équation d'équilibre résulte de l'équilibre du torseur des forces dans une section:

$$\frac{dV_{y}}{dx}=-\rho gS \„ \frac{dM_{z}}{dx}=-V_{y}$$

et s'écrit, en notant $q=-\rho gS$ la force linéique appliquée dans une section:

$$\frac{d^{2}}{dx^{2}}(EI_{zz}\frac{d^{2}v}{dx^{2}})=q$$ (4.1)

Les conditions aux limites sont des conditions d'encastrement en $x=0$

$$v(0)=0\„ \theta(0)=0$$ (4.2)

et des conditions dynamiques de force et de moment appliqués en $x=L$

$$V_{y}(L)=F \„ M_{z}(L)=0$$ (4.3)

Pour obtenir la formulation faible, on applique le théorème des travaux virtuels en calculant le travail du système pour un déplacement virtuel licite $w$ (variation du déplacement $v$). On obtiens:

$$\int_{0}^{l}\frac{d^{2}}{dx^{2}}(EI_{zz}\frac{d^{2}v}{dx^{2}})w dx=\int_{0}^{l}qw dx$$

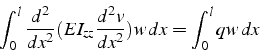
On intégre 2 fois par parties pour symétriser le problème et faire apparaıtre les conditions aux limites:

$$\int_{0}^{L}EI_{zz}\frac{d^{2}v}{dx^{2}}\frac{d^{2}w}{dx^{2}... ...\frac{d^{2}w}{dx^{2}}\frac{dw}{dx}]_{0}^{L}=\int_{0}^{L}qw dx$$

Le déplacement virtuel $w$ est une variation de $v$, et doit donc vérifier les liaisons imposées en $x=0$ (5.2), i.e:

$$w(0)=\delta v(0)=0 \mbox{ et }\frac{dw}{dx}(0)=\delta\theta(0)=0$$

Les conditions aux limites (5.3) s'écrivent en fonction de $v$:

$$-EI_{zz}\frac{d^{3}v}{dx^{3}}(L)=F, EI_{zz}\frac{d^{2}v}{dx^{2}}=0$$

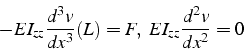
ce qui permet de calculer les intégrales de bord

$$[EI_{zz}\frac{d^{3}v}{dx^{3}}w-EI_{zz}\frac{d^{2}w}{dx^{2}}\frac{dw}{dx}]_{0}^{L}=-Fw(L)$$

La formulation faible s'écrit:

$$\mbox{Trouvez }v(x) \mbox{ t.q. }v(0)=0, \frac{dv}{dx}(0)=0$$ (4.4)

$$\int_{0}^{L}EI_{zz}\frac{d^{2}v}{dx^{2}}\frac{d^{2}w}{dx^{2}... ...L) \forall w \mbox{ t.q. }w(0)=0, \frac{dv}{dx}(0)=0$$

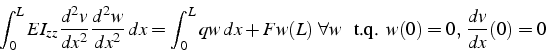
Cette formulation faible traduit l'équilibre entre le travail des forces élastiques internes et le travail des forces appliquées. Le travail des forces internes dérive d'un potentiel élastique, et cette formulation faible possède donc un Lagrangien:

$$\mathcal{L}(v)=\underbrace{-\frac{1}{2}\int_{0}^{L}EI_{zz}\l... ...x}_{U}+\underbrace{\left(\int_{0}^{L}qv dx+Fv(L)\right)}_{W}$$ (4.5)

qui correspond à la somme de l'énergie potentielle élastique $U$ et du travail $W$ des forces extérieures pour le déplacement $v$. La formulation variationnelle corresponds donc à rendre stationnaire (maximum dans notre cas) de ce Lagrangien:

$$\mbox{Trouvez }v(x) \mbox{ t.q. }v(0)=0, \frac{dv}{dx}(0)=0$$ (4.6)

$$\mathcal{L}(v)\ge\mathcal{L}(\mathtt{v}) \forall\mathtt{v} \mbox{ t.q. }\mathtt{v}(0)=0, \frac{d\mathtt{v}}{dx}(0)=0$$

et la condition de stationnarité conduit aux équations de Lagrange

$$<\frac{\partial\mathcal{L}}{\partial v},\delta v>=0 \forall\delta v \mbox{licite}$$

En utilisant la même remarque de dans le chapitre précédent, on peut déterminer la valeur de l'énergie élastique $U$ à l'équilibre, en choisissant dans la formulation faible comme variation $w$ le déplacement réel $v$.

$$U=\frac{1}{2}\int_{0}^{L}EI_{zz}\left(\frac{d^{2}v}{dx^{2}}\right)^{2} dx=\frac{1}{2}\int_{0}^{L}qv dx+\frac{1}{2}Fv(L)$$

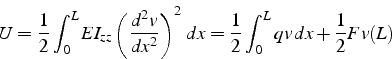
C'est le travail moyen fournit par les forces extérieures pour passer de l'état naturel (sans contrainte) à l'état d'équilibre contraint en augmentant progressivement les forces extérieures de $0$ à leurs valeurs finales. C'est ce travail fourni par les forces extérieures qui est transformé en énergie élastique. On constate aussi que dans le Lagrangien, le terme de travail des forces extérieures ne correspond pas au travail fournit, mais à un travail virtuel associé au déplacement $v$ (dans ce cas le travail fournit est en fait égal à la moitié de cette valeur).

La valeur minimum du Lagrangien est égale à l'énergie potentiel élastique $U$:

$$\mathcal{L}(v)=-U+W=-U+2U=U$$