suivant: 2. Algorithmique monter: 1. Préambule précédent: 1.3 Démarche du calcul Table des matières
Un pendule de masse m est fixé au bout d'une tige rigide de longueur l (sans masse). L'autre extrémité de la tige est fixée sur une table vibrante verticalement, dont le mouvement est sinusoıdale de la forme:
![\includegraphics[width=0.4\textwidth]{pendule}](img5.png)
En l'absence de mouvement de la table, le pendule tombe sous l'effet de la gravité.
Si la table vibre, le mouvement de la table en O est transmis par
la tige au point M du pendule, et génère une accélération qui vient
compensé la gravité. Pour éviter que le pendule ne tombe, il faut
que la fréquence de vibration de la table ![]() soit beaucoup
plus grande que la fréquence d'oscillation du pendule simple
soit beaucoup
plus grande que la fréquence d'oscillation du pendule simple
![]() avec
avec
![]()
Le bilan des forces s'exerçant sur le centre de gravité du pendule
![]() :
:
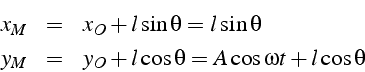
L'accélération
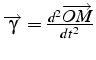 est obtenue en dérivant deux fois par rapport au temps la position.
est obtenue en dérivant deux fois par rapport au temps la position.
Pour éliminer la tension
![]() , on projeté l'équation
de la dynamique (1.1) suivant la direction tangentielle:
, on projeté l'équation
de la dynamique (1.1) suivant la direction tangentielle:
ce qui nous fournit une équation différentielle du second ordre en
![]() , que l'on ne sait pas résoudre analytiquement.
, que l'on ne sait pas résoudre analytiquement.
Pour résoudre numériquement l'équation, il faut se fixer des valeurs de paramètres.
On fixe la fréquence d'oscillations libres du pendule, i.e. ![]() en fixant la longueur de la tige
en fixant la longueur de la tige ![]() (avec
(avec ![]() ):
):
L'amplitude des oscillations de la table est choisie petite devant
![]() : i.e.
: i.e. ![]() .
.
Il reste donc à fixer la pulsation ![]() des oscillations de la
table, qui est le paramètre de l'étude. On étudiera 3 cas:
des oscillations de la
table, qui est le paramètre de l'étude. On étudiera 3 cas:
Pour valider , on peut comparer la solution calculée avec la solution du pendule simple en petites oscillations. Pour cela on considère que l'angle
est petit. Dans ce cas le pendule oscille de façon sinusoıdale
avec une pulsation ![]()
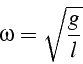
![\begin{algor}[1]
\item [{Définir}] X1,Y1,G1,G2,GT : fonction réelle de t
\item [...
...\leftarrow$resolution(EDP,CI)
\item [{{*}}] trace(theta(t),t=0..10);
\end{algor}](img37.png)
Après cette analyse, on étudie la stabilité du pendule oscillant en utilisant Maple pour les calculs et la résolution numérique.
Un pendule de masse m est fixé au bout d'une tige rigide de longueur
l (sans masse). L'autre extrémité de la tige est fixée sur une table
vibrante verticalement, dont le mouvement est ![]() .
.
On se propose d'étudier le mouvement avec Maple en fonction de la
fréquence de vibration ![]() de la table. Ce problème est un exemple
classique de stabilité de système mécanique.
de la table. Ce problème est un exemple
classique de stabilité de système mécanique.
Pendule oscillant: execution avec Maple
Pendule oscillant: (version HTML)