Initialisation
| > | restart:interface( warnlevel=0 ):with(plots):with(plottools):
# fonction de trace du systeme TracePendule:=proc(t,angle,l,A,omega) local x1,y1,y2,tige,boule,anim; y2:=A*cos(omega*t); x1:=l*sin(angle); y1:=l*cos(angle)+y2; tige:=curve([[0,y2],[x1,y1]],color=green,thickness=2); boule:=disk([x1,y1], 0.005, color=red); tab:=rectangle([-0.01,y2-0.01],[0.01,y2],color=black): anim:=display(tige,boule,tab); end proc: display(TracePendule(0,Pi/10,0.1,0.01,150),scaling=constrained,axes=none); |
![[Plot]](images/Pendule_1.gif)
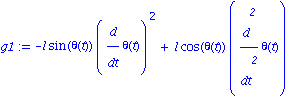
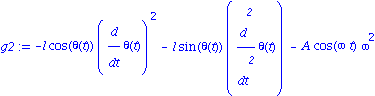
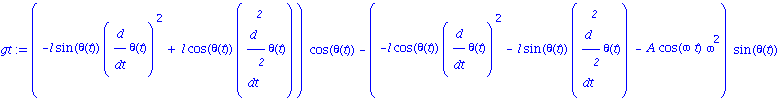
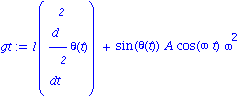
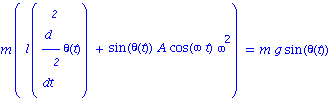
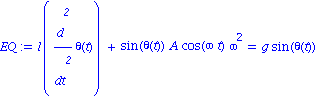
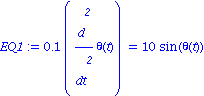
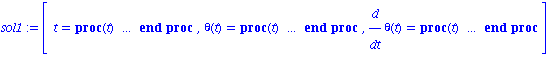
![[Plot]](images/Pendule_19.gif)
![[Plot]](images/Pendule_22.gif)
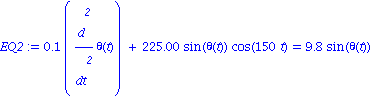
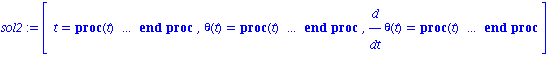
![[Plot]](images/Pendule_29.gif)
![[Plot]](images/Pendule_30.gif)
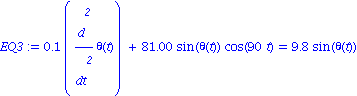
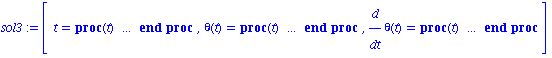
![[Plot]](images/Pendule_37.gif)
![[Plot]](images/Pendule_40.gif)