monter: 9. Variables de Couplage précédent: 9.3 Couplage par extrusion Table des matières
On va utiliser une variable de couplage pour traiter le problème de contrôle de la température dans le cas d'un radiateur de micro-processeur (7).
Pour cela on mesure la température ![]() en un point sur le
micro-processeur, et on asservie le ventilateur, c'est à dire le coefficient
en un point sur le
micro-processeur, et on asservie le ventilateur, c'est à dire le coefficient
![]() d'échange par convection:
d'échange par convection:
où la fonction ![]() est la fonction de contrôle, comprise entre
0 et 1,
est la fonction de contrôle, comprise entre
0 et 1, ![]() le coefficient d'échange sans le radiateur et
le coefficient d'échange sans le radiateur et ![]() le coefficient d'échange avec le ventilateur au maximum.
le coefficient d'échange avec le ventilateur au maximum.
L'asservissement utilise un contrôle PI (proportionnel-intégrale),
au lieu d'un simple contrôle on/off. On utilise un contrôle fonction
![]() fonction l'écart mesurée
fonction l'écart mesurée
![]() où
où ![]() est la température de fonctionnement, et de l'intégrale de l'écart:
est la température de fonctionnement, et de l'intégrale de l'écart:
Ainsi pour une croissance linéaire de l'erreur: ![]() ,
le contrôle a pour expression:
,
le contrôle a pour expression:
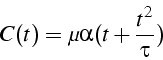
Le paramètre ![]() contrôle donc l'amplitude et
contrôle donc l'amplitude et ![]() le temps
de relaxation.
le temps
de relaxation.
Pour calculer l'intégrale dans (9.1), on introduit la solution
![]() de l'équation différentielle
de l'équation différentielle
ce qui permet d'écrit le contrôle ![]() sous la forme:
sous la forme:
La valeur du coefficient d'échange ![]() est alors fonction de
est alors fonction de
![]() par la loi
par la loi
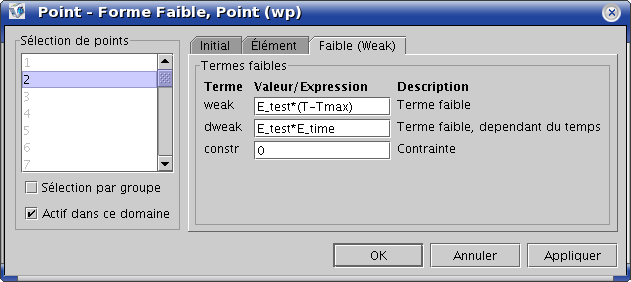
Dans FEMLAB on introduit une variable supplémentaire E en un point (“multiphysique-> ajouter->Forme Faible (point)”), solution de l'équation différentielle (9.2), dont la formulation faible s'écrit:
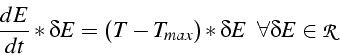
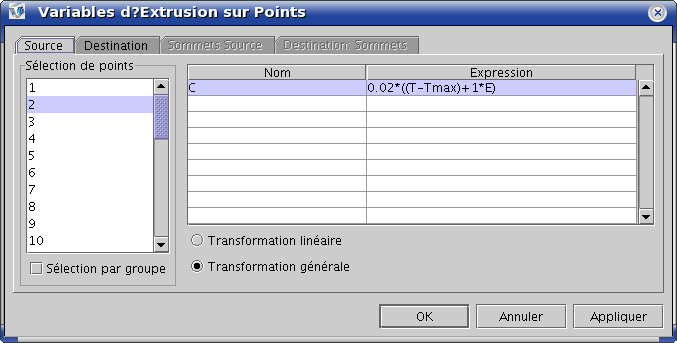
On définit ensuite une variable de couplage ![]() fonction de
fonction de ![]() et de
et de ![]() au point de contrôle pour que le contrôle soit définie
dans tout le domaine.
au point de contrôle pour que le contrôle soit définie
dans tout le domaine.
Les courbes ci-dessous montrent l'effet de se contrôle sur la température
au point de contrôle, la valeur du contrôle ![]() et la valeur résultante
de
et la valeur résultante
de ![]() en fonction du temps.
en fonction du temps.
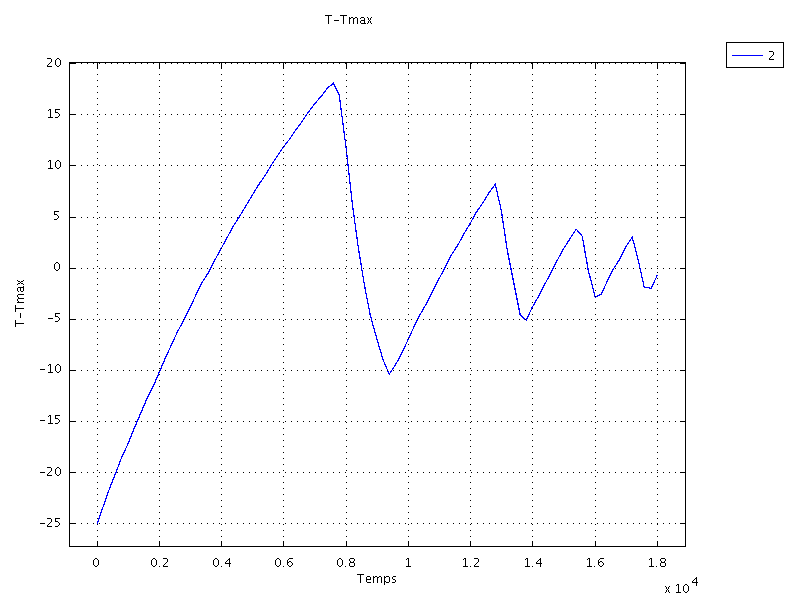
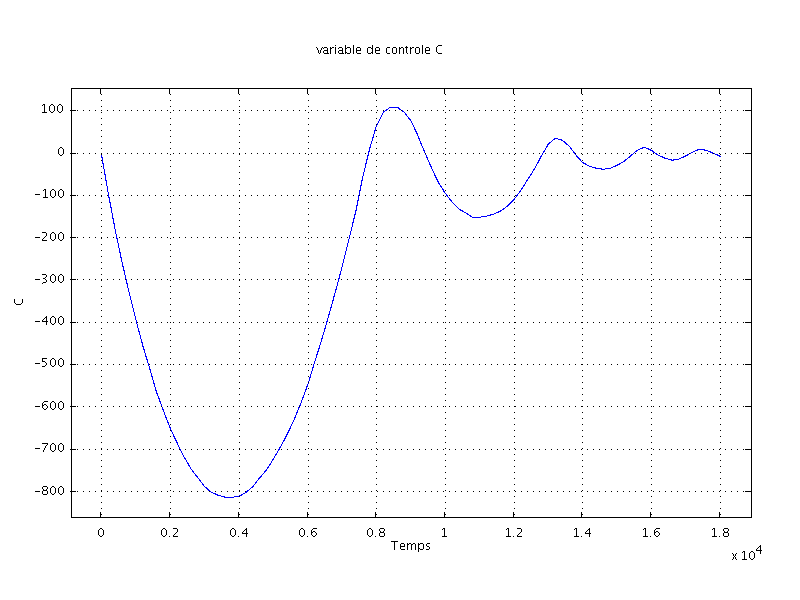
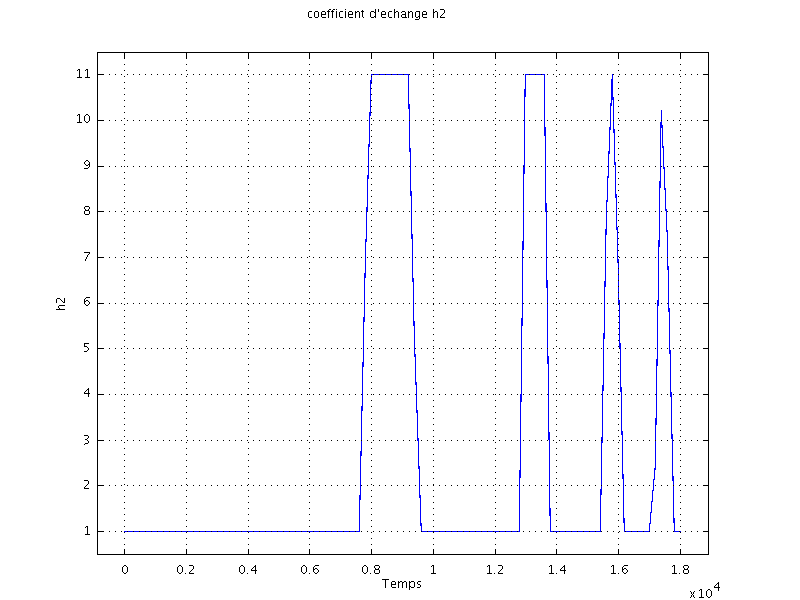
Sur le dernier graphe, on visualise la mise en route et l'arrêt du ventilateur.
description du modele FEMLAB (version HTML)