9.2 Couplage intégrale

On se propose de déterminer la solution $u(x,y)$ du problème de Poisson suivant sur le cercle unité $\Omega$:

$$\begin{eqnarray*} -\Delta u & = & 1+\int_{\Omega}u d\Omega\\ u_{\Gamma} & = & 0\end{eqnarray*}$$

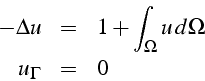
Le second membre dépend de l'intégrale de la solution $u$. Pour le résoudre on introduit une variable de couplage $U_{m}$

$$U_{m}=\int_{\Omega}u d\Omega$$

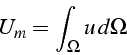
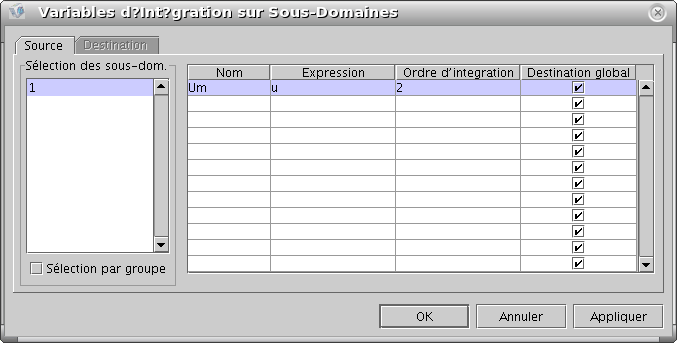
dans le modèle FEMLAB, que l'on introduit dans le second membre de l'équation de Poisson (menu “options->variables de couplage d'intégration->sous domaine”).

On sélectionne un modèle de résolution non-linéaire pour que cette variable $U_{m}$soit calculée correctement.

La solution calculée vérifie:

$$\begin{eqnarray*} \int_{\Omega}u d\Omega & = & 0.646628\\ \int_{\Gamma}\frac{\partial u}{\partial n} d\Gamma & = & -5.168337\end{eqnarray*}$$

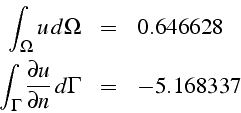
En intégrant l'équation et avec la formule de Green, on a:

$$\int_{\Omega}-\Delta u d\Omega=-\int_{\Gamma}\frac{\partial u}{\partial n} d\Gamma=\int_{\Omega}(1+U_{m})d\Omega$$

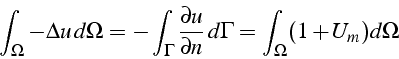
et on vérifie que :

$$5.1683337\approx\pi(1+0.646628)=5.17303$$

De même le tracé de $-\Delta u$ montre une valeur égale à $1+Um\approx1.6466$ (sauf près des bords).

9.2.1 modèle FEMLAB

description du modele FEMLAB

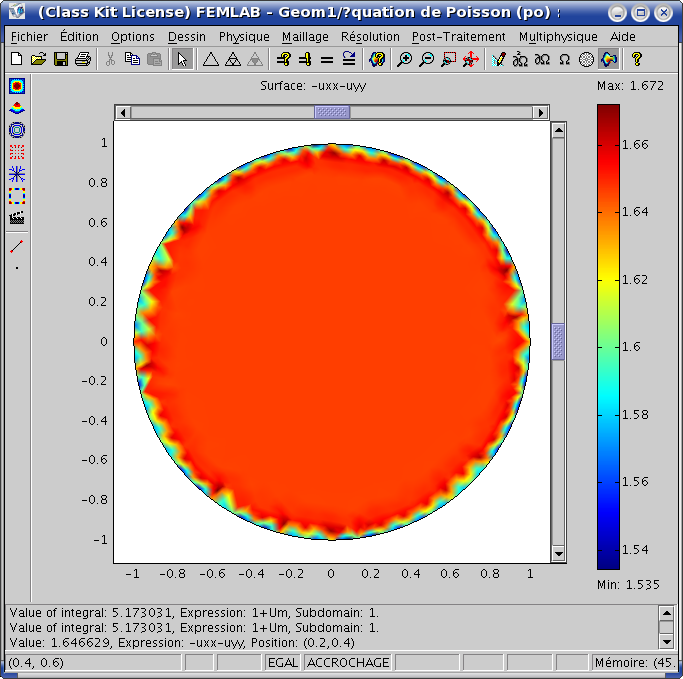
description du modele FEMLAB (version HTML)