suivant: 5. Un second exemple monter: 4. Méthode des éléments précédent: 4.2 Première approche avec Table des matières
La précision d'un calcul numérique dépend de plusieurs facteurs, parmis lesquels:
L'erreur due au choix du modèle mathématique dépend évidemment du problème physique.
L'erreur de discrétisation dépend du choix de la méthode numérique utilisée. Dans la cas des éléments finis, elle dépend:
Pour un triangle ![]() , on définit la taille
, on définit la taille ![]() comme la
longueur du plus grand coté (figure ci-dessous).
comme la
longueur du plus grand coté (figure ci-dessous).
![\includegraphics[scale=0.3]{CHAP1/triangle}](img408.png)
On définit aussi le diamètre ![]() du cercle inscrit et le diamètre
du cercle inscrit et le diamètre
![]() du cercle circonscrit, ainsi que le rapport d'aspect du triangle
du cercle circonscrit, ainsi que le rapport d'aspect du triangle
![]() . Pour un triangle équilatéral, on a
. Pour un triangle équilatéral, on a ![]() et
et
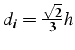 , donc
, donc
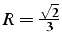 . Par
contre pour un triangle de plus en plus aplati, le rapport d'aspect
tend vers 0 (car
. Par
contre pour un triangle de plus en plus aplati, le rapport d'aspect
tend vers 0 (car
![]() ) , ce qui indique la dégénérescence
du triangle.
) , ce qui indique la dégénérescence
du triangle.
Avec ces définitions, on montre que l'erreur d'interpolation
![]() sur un triangle vérifie une relation du type:
sur un triangle vérifie une relation du type:
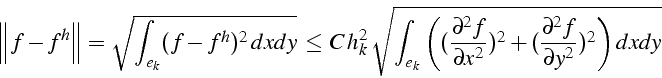
Cependant la constante ![]() dépend du rapport d'aspect
dépend du rapport d'aspect ![]() et l'estimation
d'erreur dégénère lorsque
et l'estimation
d'erreur dégénère lorsque ![]() , i.e. lorsque le triangle
devient de plus en plus aplatis.
, i.e. lorsque le triangle
devient de plus en plus aplatis.
Sous FEMLAB, la qualité du maillage permet d'avoir une idée sur la
valeur de ce rapport d'aspect ![]() . Pour cela, on calcul sur chaque
élément la valeur suivante, fonction de l'aire
. Pour cela, on calcul sur chaque
élément la valeur suivante, fonction de l'aire ![]() et de la longueur
des cotés
et de la longueur
des cotés
![]() :
:
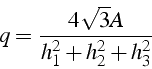
qui varie de 0 (si le triangle est dégénérée) à 1 (pour un triangle
équilatéral
![]() et
et
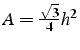 ).
Un bon maillage nécéssite en générale une valeur
).
Un bon maillage nécéssite en générale une valeur ![]() .
.