suivant: 3.2 Méthode de Bissection monter: 3. Recherche des racines précédent: 3. Recherche des racines Table des matières
Soit un mobile ayant une trajectoire donnée par la fonction ![]() ,
avec
,
avec
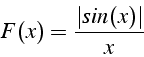
On veut déterminer la position ![]() du point de cette trajectoire
correspondant à une hauteur
du point de cette trajectoire
correspondant à une hauteur ![]() fixée:
fixée:
![\includegraphics[width=0.5\textwidth]{CHAP2/courbe}](img82.png)
Pour résoudre le problème on localise la ou les racines par l'étude
de la fonction ![]()
englishanalyse de la fonction avec le tableau de variations