7.7 Structures de données

Maple sait manipuler des séquences (seq), des listes (list), des ensembles (set), des tables (table) et des tableaux (array).

Une séquence est simplement un succession de valeurs séparées par une , . La fonction seq permet de générée des séquences simplement:

>n:=10: seq(i/n,i=0..n);

$$0,\frac{1}{10},\frac{1}{5},\frac{3}{10},\frac{2}{5},\frac{1}{2},\frac{3}{5},\frac{7}{10},\frac{4}{5},\frac{9}{10},1$$

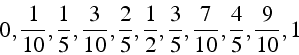
que l'on peut transformer en liste en entourant le résultat avec les symboles et

>L:=[%]; L[3];

$$L:=[0,\frac{1}{10},\frac{1}{5},\frac{3}{10},\frac{2}{5},\frac{1}{2},\frac{3}{5},\frac{7}{10},\frac{4}{5},\frac{9}{10},1]$$

$$\frac{1}{5}$$

ou en ensemble (liste non ordonnée dans laquelle les entrées identiques sont supprimées) en entourant le résultat avec les symboles et :

>E:={%%%};E[3];

$$E:=\{0,1,\frac{1}{2},\frac{2}{5}\frac{1}{10},\frac{3}{10},\frac{1}{5},\frac{3}{5},\frac{7}{10},\frac{4}{5},\frac{9}{10}\}$$

$$\frac{1}{2}$$

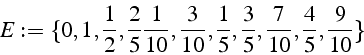
Les tableaux sont la base de la manipulation des vecteurs et des matrices. Pour cela on utilise la librairie Maple linalg (il existe maintenant sous Maple une nouvelle librairie LinearAlgebra pour manipuler plus efficacement des matrices de type particulier (bande, tri-diagonale, ..)). Pour utiliser une librairie sous Maple, on doit la déclarer avec la fonction with(xxx) où xxx est le nom de la librairie.

>with(linalg):

Pour déclarer un vecteur on utilise la fonction vector :

>X:=vector(10); Y:=vector(3,[1,2,3]);

$$X:=array(1..10,[])$$

$$Y:=[1,2,3]$$

On a déclarer un vecteur X de 10 éléments non initialisés et un vecteur Y de 3 éléments initialisés. Pour obtenir la valeur d'un élément on utilise l'indice entre [ ]:

>X[2],Y[2];

$$X_{2},3$$

De même pour les matrices, on utilise matrix:

>A:=matrix(3,3,1.0): M:=matrix(2,2,[[2,1],[1,2]]);

$$M:=\left[\begin{array}{cc} 2 & 1\\ 1 & 2\end{array}\right]$$

Pour accéder à un élément d'une matrice, on met les 2 indices entre [ ].

>M[2,2];

$$2$$

On note que les indices des vecteurs et des matrices commencent à 1. Pour afficher la valeur d'un vecteur ou d'une matrice on utilise la fonction evalm:

>A=evalm(A);

$$A=\left[\begin{array}{ccc} 1 & 1 & 1\\ 1 & 1 & 1\\ 1 & 1 & 1\end{array}\right]$$

La multiplication matrice vecteur est notée et on doit utiliser evalm pour afficher le résultat:

>evalm(A&*Y);

$$[6,6,6]$$

Pour résoudre un système linéaire, on utilise la fonction linsolve:

>linsolve(B,[1,2]);

$$[0,1]$$