7.6 Calcul différentiel et intégrale

Les fonctions pour le calcul différentiel et intégrale sous Maple sont:

Notation Maple

Signification

Notation mathématique diff(f(x),x);

Ces fonctions existent aussi avec une majuscule : Diff, Int, Sum . C'est la forme inerte et dans ce cas l'expression n'est pas évaluée.

>f:= x*sin(a*x)+b*x^2;

$$f:=x\sin(xa)+bx^{2}$$

>df:=diff(f,x);

$$df:=\sin(xa)+x\cos(xa)a+2bx$$

la fonction diff effectue la dérivation d'une expression par rapport à une variable. Pour obtenir la fonction dérivée, il faut transformer l'expression en fonction, ou utiliser l'opération $D$ de différenciation de fonction, qui permet directement de calculer la valeur de la dérivée:

>D(x->x*sin(a*x))(Pi);

$$\sin(a\pi)+\pi\cos(a\pi)a+2b\pi$$

>int(df,x); simplify(%);

$$-\frac{\cos(xa)}{a}+\frac{(xa)+xa\sin(xa)}{a}bx^{2}$$

$$x(\sin(xa)+bx)$$

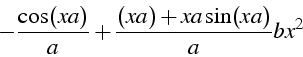
On note que l'on a été obliger de simplifier l'expression pour retrouver le résultat initial. Pour une intégrale définie, on spécifie les bornes:

>int(df,x=1..2);

$$2\sin(2a)+3b-\sin(a)$$

Pour obtenir un calcul numérique de la dérivée, on utilise la fonction evalf , avec soit la fonction int si on évalue numériquement le résultat du calcul annalytique de l'intégrale, soit Int pour calculer une valeur approchée de l'intégrale:

>evalf(int(exp(-x^2),x=0..1);

$$.7468241330$$

>evalf(Int(exp(-x^),x=0..1);

$$.74682341328$$

Dans le premier calcul, on évalue le résultat de l'intégration $\frac{1}{2}erf(1)\sqrt{\pi}$ , alors que dans le second on calcule une valeur approchée de l'intégrale.

Le calcul de cette intégrale par une méthode de trapèzes sur N intervalles s'écrit, en utilisant la fonction sum:

>N:=100: h:=1.0/N: sum((exp(-((i-1)*h)^2)+exp(-(i*h)^2)*h/2, i=1..N);

$$.7468180010$$

Le résultat est moins précis que le précèdent, ce qui montre que l'intégration numérique dans Maple est relativement précise et sophistiquée (quadrature de Clenshaw-Curtis avec détection des singularités).

Le développement en série de Taylor au voisinage de $x=0$ s'écrit:

>series(f,x=a);

$$(a+b)x^{2}-\frac{1}{6}a^{3}x^{4}+\theta(x^{6})$$

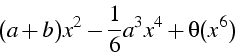
que l'on peut transformer en polynôme à l'aide de la fonction convert :

>convert(%,polynom);

$$(a+b)x^{2}-\frac{1}{6}a^{3}x^{4}$$