4.5 Chocs obliques

Un choc oblique est créé lorsqu'un écoulement supersonique est défléchi (par un obstacle). Un écoulement supersonique de vitesse $U_{1}$ est défléchi par une rampe d'angle $\theta$. Un choc oblique d'angle $\beta$ apparaıt pour permettre à l'écoulement d'avoir une vitesse $U_{2}$ parallèle à la rampe.

La géométrie du choc oblique est donnée sur la figure ci-dessous

On décompose la vitesse $U$ suivant la direction normale au choc $U_{n}$ et la direction tangente au choc $U_{t}$.

On choisit un volume de contrôle entourant le choc (voir figure) et d'épaisseur fine. On intègre ensuite les équations de bilan stationnaire sur ce volume, en notant que pour la quantité de mouvement, le flux a 2 composantes. En effet le flux de quantité de mouvement à travers une surface de normale $\overrightarrow{n}$ s'écrit:

$$\rho(\overrightarrow{U}\otimes\overrightarrow{U}).\overright... ...array}{c} \rho U_{n}^{2}+p\\ \rho U_{n}U_{t}\end{array}\right]$$

1. bilan de masse:
   
   

   $$\rho_{1}U_{n1}=\rho_{2}U_{n2}$$ (4.10)

   
   

2. bilan de quantité de mouvement suivant la normale:
   
   

   $$\rho_{1}U_{n1}^{2}+p_{1}=\rho_{2}U_{n2}^{2}+p_{2}$$ (4.11)

   
   

3. bilan de quantité de mouvement suivant la tangente:
   
   

   $$\rho_{1}U_{n1}U_{t1}=\rho_{2}U_{n2}U_{t2}$$ (4.12)

   
   

4. conservation de l'enthalpie totale:
   
   

   $$h_{1}+\frac{U_{n1}^{2}+U_{t1}^{2}}{2}=h_{2}+\frac{U_{n2}^{2}+U_{t2}^{2}}{2}$$ (4.13)

   
   

En utilisant l'équation 4.10, la relation 4.12 implique la conservation de la vitesse tangentielle $U_{t1}=U_{t2}$ , et on constate alors que le système d'équation est identique à celui du choc droit, en remplaçant simplement dans les équations les vitesses $U_{1}$ et $U_{2}$ par les vitesses normales $U_{n1}=U_{1}\sin\beta$ et $U_{n2}=U_{2}\sin\beta$. Les relations de choc pour un choc oblique sont données par les relations (4.4,4.5,4.6) le nombre de Mach $M_{1}$ par le nombre de Mach “normal” $M_{n1}=\frac{U_{n1}}{c_{1}}=M_{1}\sin\beta$ et le nombre de Mach $M_{2}$ par le nombre de Mach “normal” $M_{n2}=\frac{U_{n2}}{c_{2}}=M_{2}\sin(\beta-\theta)$.

De cette analogie avec le choc droit, on en déduit que pour un choc oblique, le Mach “normal” aval $M_{n2}$ doit être subsonique, mais l'écoulement aval peut rester supersonique (et le reste en général).

L'angle de déflection de l'écoulement $\theta$ vérifie:

$$\theta=\beta-\tan^{-1}\frac{U_{n_{2}}}{U_{t}}=\tan^{-1}\frac{U_{n_{1}}}{U_{t}}-\tan^{-1}\frac{U_{n_{2}}}{U_{t}}$$

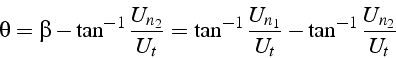
Pour une valeur $U_{n1}$ et $U_{n2}$ fixée, i.e. une intensité de choc fixé, la courbe $\theta(U_{t})$ présente un maximum pour $U_{t}=\sqrt{U_{n1}U_{n2}}$. Cela veut dire que pour une intensité de choc donnée, il existe une valeur maximale de la déflexion $\theta_{max}$ . Ainsi pour un nombre de Mach $M_{1}=3$ , on a $\theta_{max}=36^{\circ}$.

Si on trace le diagramme de vitesse $\frac{U_{2}}{U_{1}}$ pour un nombre de Mach amont $M_{1}$ fixé, dans des axes $\frac{U_{2x}}{U_{1}}$(projection suivant l'axe $x$ parallèle à $U_{1}$) et $\frac{U_{2y}}{U_{1}}$(projection suivant l'axe $y$), on obtient une polaire des vitesses pour le choc oblique.

Rem: on a $\frac{U_{n2}}{U_{n1}}=F(M_{1},\beta)$ d'après 4.4, et $U_{t2}=U_{t1}=U_{1}\cos\beta$, d'où l'on déduit par projection suivant les axes $Ox$ et $Oy$ les composantes de $U_{2}$ : $\frac{U_{2x}}{U_{1}}=F(M_{1},\beta)$ et $\frac{U_{2y}}{U_{1}}=G(M_{1},\beta)$ . Pour une valeur fixé de $M_{1}$, on en déduit donc pour chaque valeur de $\beta$ (angle du choc) les composantes de la vitesse avale $U_{2}$, et donc l'angle de déflexion $\theta=arctg\frac{U_{2y}}{U_{2x}}$.

Sur cette polaire, on constate que pour un angle de déviation $\theta$ donné, il existe 2 solutions:

1. un choc faible correspondant à la vitesse $U_{2}$ la plus grande: la décélération du fluide est dans ce cas la plus faible et l'écoulement reste en général supersonique après le choc. C'est la configuration que l'on rencontre le plus souvent.
2. un choc fort correspondant à la vitesse $U_{2}$ la plus faible: la décélération du fluide est plus forte et l'écoulement est alors subsonique après le choc.

On note aussi sur le diagramme, l'existence d'une valeur maximale $\theta_{max}$ de la déflexion. Dans le cas où on veut imposer une déflexion de l'écoulement avec une valeur supérieure à $\theta_{max}$, cela ne peut plus se faire avec un choc oblique faible attaché, mais à travers un choc courbe fort détaché (voir ci dessous).