synthèse réaliste ?
au minimum, on souhaite dessiner des objets et les éclairer correctement. ce qui suppose que l'on sait dessiner les objets mais aussi déterminer lesquels sont éclairés, ou à l'ombre, et comment ils réfléchissent la lumière reçue vers l'observateur, ou la camera.
il y a, en gros, 2 manières assez différentes de dessiner les objets, cf introduction api 3d, openGL et pipeline graphique et principes du lancer de rayons. Mais dans les 2 cas, on obtient finalement les mêmes informations : quel point de quel objet est visible pour chaque pixel de l'image, la normale de la surface de l'objet pour ce point et la description de sa matière.
1 source
on va commencer par un cas simple : une seule source qui émet de la lumière le long d'une seule direction, un peu comme le soleil. c'est la situation habituelle, cf lumière et matière : on a une camera, un point dans la scène, et une direction vers la source de lumière :
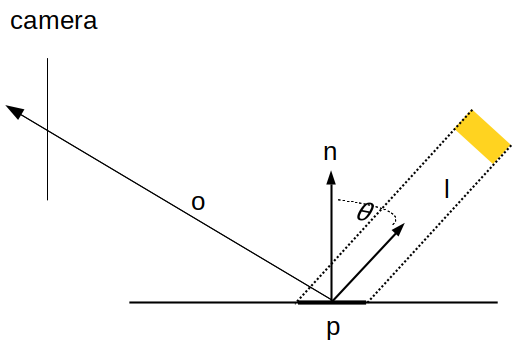
qu'est ce que l'on calcule ?
\[ L_r(p, \vec{o})= \frac{k}{\pi} V(\vec{l}) L_i(p, \vec{l}) \cos \theta \]
ou de manière plus lisible, \( L_r(p, \vec{o}) \) la lumière réfléchie par p vers l'observateur dans la direction o se calcule comme la réflexion de la
lumière incidente \( L_i(p, \vec{l}) \) qui éclaire le point p depuis la direction l. \( V(p, \vec{l}) \) est égal à 1 si la source qui émet la lumière est visible depuis p dans la direction l et 0 si ce n'est pas le cas. Le dernier terme, \( k / \pi \) représente une réflexion diffuse toute simple, cf le modèle de Lambert dans lumière et matière.
on peut écrire un code simplifié pour réaliser ce calcul :
et voila !

c'est moche, mais c'est correct.
pourquoi ? habituellement, il y a de la lumière partout, ie cette situation n'est pas très naturelle, le ciel éclaire presque autant que le soleil.
un ciel / dome de directions
comment éclairer les objets par un ciel ? assez intuitivement, on a envi de refaire le calcul avec plusieurs directions. plus précisement, il va falloir intégrer (ou sommer) toute la lumière qui éclaire le point quelque soit sa direction d'incidence. cette formulation s'appelle l'équation du rendu :
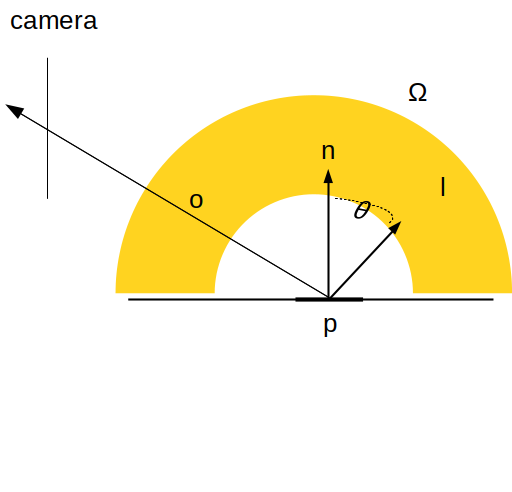
cette formulation de la synthèse d'images réaliste à été introduite en 1986 par J. Kajiya, cf "The rendering equation".
\[ L_r(p, \vec{o})= \int_{\Omega} \frac{k}{\pi} V(\vec{l}) L_i(p, \vec{l}) \cos \theta dl \]
le symbole \( \Omega \) représente toutes les directions \( \vec{l} \) qui peuvent éclairer le point p.
c'est malin, comment faire le calcul maintenant ? si on suppose qu'il n'y a pas d'ombres, ie \( V(p)= 1 \) pour toutes les directions de \( \Omega \), on peut quand même faire le calcul et le résultat est plutot simple et facile à retenir :
\[ \begin{eqnarray*} L_r(p, \vec{o}) &= & \frac{k}{\pi} \int_{\Omega} L_i(p, \vec{l}) \cos \theta dl\\ &= & \frac{k}{\pi} L_i(p, \vec{l}) \frac{1 + \cos \theta}{2}\\ \mbox{avec }\vec{l} &= & \mbox{Y (ou la direction vers le sommet du dome)} \end{eqnarray*} \]
pour les curieux : les détails des calculs sont dans "Area Light Sources for Real-Time Graphics", 1996, J.Snyder

et pour de vrai ? (avec les ombres)
comment estimer numériquement l'intégrale d'une fonction ? par exemple :
\[ \int_a^b f(x) dx = ? \]
en 1d, on peut utiliser l'intégration par rectangles. l'idée est de découper le domaine d'intégration, un intervalle \( [a .. b] \) en N segments, chaque segment mesure \( \frac{1}{N}(b - a) \) :
\[ \begin{eqnarray*} \int_a^b f(x) dx &= & \frac{1}{N} \sum_i^N (b-a) f(x_i)\\ \mbox{et }x_i &= & a + \frac{1}{N}(b - a) \cdot i \end{eqnarray*} \]
en 2d, pour utiliser la même méthode, il faut découper le domaine d'intégration (un rectangle) en grille de \( N \) cases. mais on veut intégrer sur \( \Omega \), un dome / une hemisphère / un ensemble de directions... et construire une grille sur un ensemble de directions n'est pas très direct, ni très intuitif.
mais bien sur, il y a une solution : on peut utiliser une spirale de Fibonacci qui permet de construire l'équivalent d'une grille sur \( \Omega \) : cf "Spherical Fibonacci Point Sets for Illumination Integrals", 2013, R.Marques, C.Bouville, R.Ribardière, L.PSantos, K. Bouatouch.
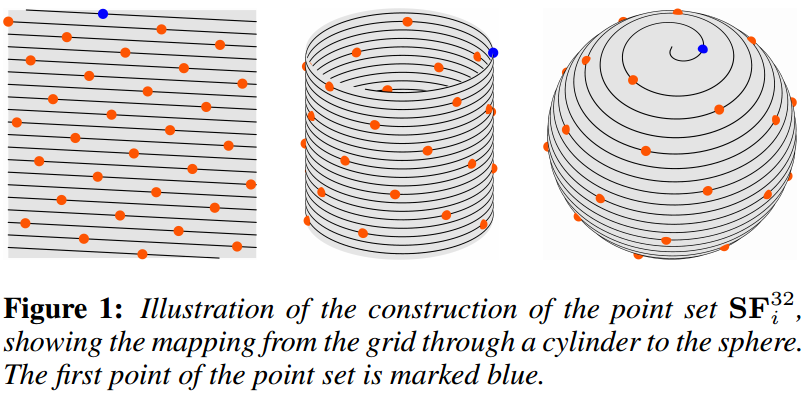
pour construire la direction \( i \) sur \( N \) :
\[ \begin{eqnarray*} \cos \theta &= & 1 - \frac{2i + 1}{2N}\\ \phi &= & 2 \pi \left[ \frac{i}{\Phi} \right] \equiv 2 \pi \left( \frac{i}{\Phi} - \left\lfloor \frac{i}{\Phi} \right\rfloor \right)\\ \mbox{avec }\Phi &= &\frac{(\sqrt 5 + 1)}{2}\\ \mbox{avec }\sin \theta&= &\sqrt{1 - \cos^2 \theta} \end{eqnarray*} \]
il ne reste plus qu'à passer des angles \( (\theta, \phi) \) aux coordonnées \( (x, y, z) \) :
\[ (x, y, z) = (\cos \phi \sin \theta, \sin \phi \sin \theta, \cos \theta) \]
ce qui se code sans trop de problèmes :
on peut maintenant estimer l'intégrale !
\[ \begin{eqnarray*} L_r(p, \vec{o}) &= & \int_{\Omega} \frac{k}{\pi} V(\vec{l}) L_i(p, \vec{l}) \cos \theta dl\\ &= & \frac{1}{N} \sum_i^N \frac{k}{\pi} V(\vec{f_i}) L_i(p, \vec{f_i}) \cos \theta\\ \mbox{avec }\vec{f_i} &= & \mbox{fibonacci(i, N)} \end{eqnarray*} \]
et voila !

avec un code assez direct :
et alors ?
c'est fini ? tout marche parfaitement ?
pas vraiment, j'ai omis un détail important, quelle valeur utiliser pour \( N \) ? le nombre de directions utilisé pour estimer l'intégrale... l'impact sur le résultat est loin d'être négligeable... et sur le temps de calcul aussi, bien sur.
voila quelques exemples avec \( N= 1, 4, 16, 64 \)
 |  |
 |  |
et \( N= 256 \) :

euh c'est toujours moche ? oui, les directions de la spirale sont les mêmes pour tous les points. lorsqu'il n'y a pas assez de directions (moins de 256 dans cet exemple) pour estimer précisement l'intégrale, il y a des défauts dans les images... une superposition d'ombres un peu bizarre, dans ce cas. mais on peut casser ces défauts en faisant tourner la spirale sur elle même, différemment pour chaque point. ca ne change pas le résultat, mais au lieu d'obtenir une superposition un peu bizarre, on obtient du bruit à la place, ce qui est finalement moins génant. de plus, on pourra filtrer ce bruit si nécessaire, alors que ce serait particulièrement difficile sinon.
 |  |
 |  |
et \( N= 256 \) :

résumé
on vient de voir très rapidement 2 choses : comment formuler le problème, et une méthode numérique pour estimer le résultat.
on peut considérer que sur ce type de scène éclairée par un ciel / toutes les directions d'une hemisphère, la solution proposée est correcte. mais bien sur, toutes les scènes ne sont pas en extérieur et éclairées par le ciel et le soleil. que se passe-t-il dans une pièce éclairée par une source au plafond ?
voila quelques exemples de la fonction intégrée pour un point dans le même exemple. l'image représente une vue de la scène, un rayon, un point de calcul et la vignette en bas à gauche est une vue 'fisheye' des objets et des sources visibles par le point (les sources de lumières sont en blanc dans les vignettes)
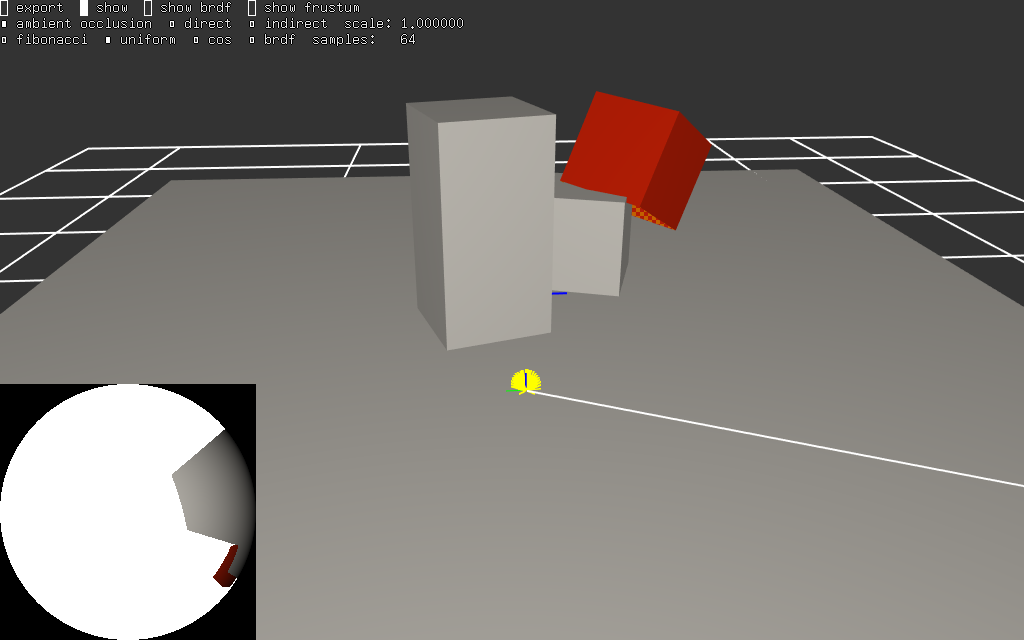 | 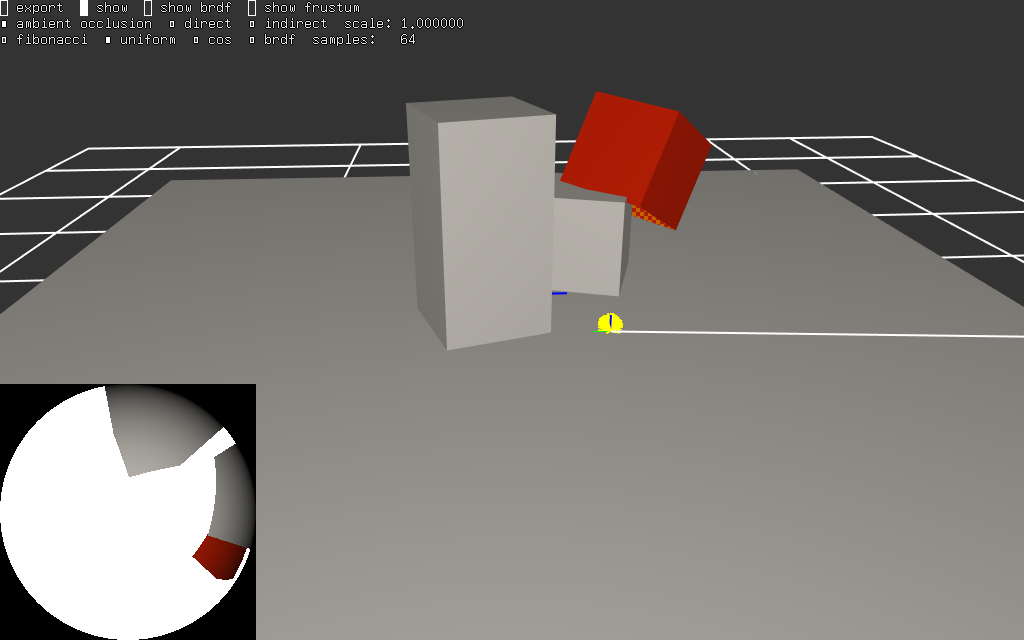 |
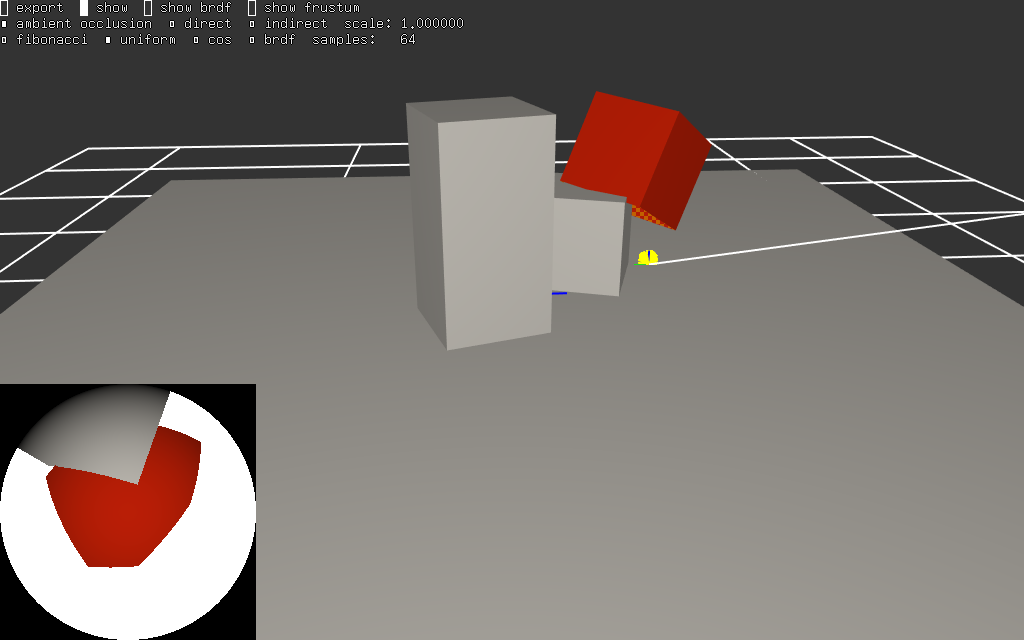
premier constat, il y a de la lumière partout (ou presque) ! c'est normal, le ciel éclaire la scène...
et dans une scène intérieure éclairée par une source au plafond :
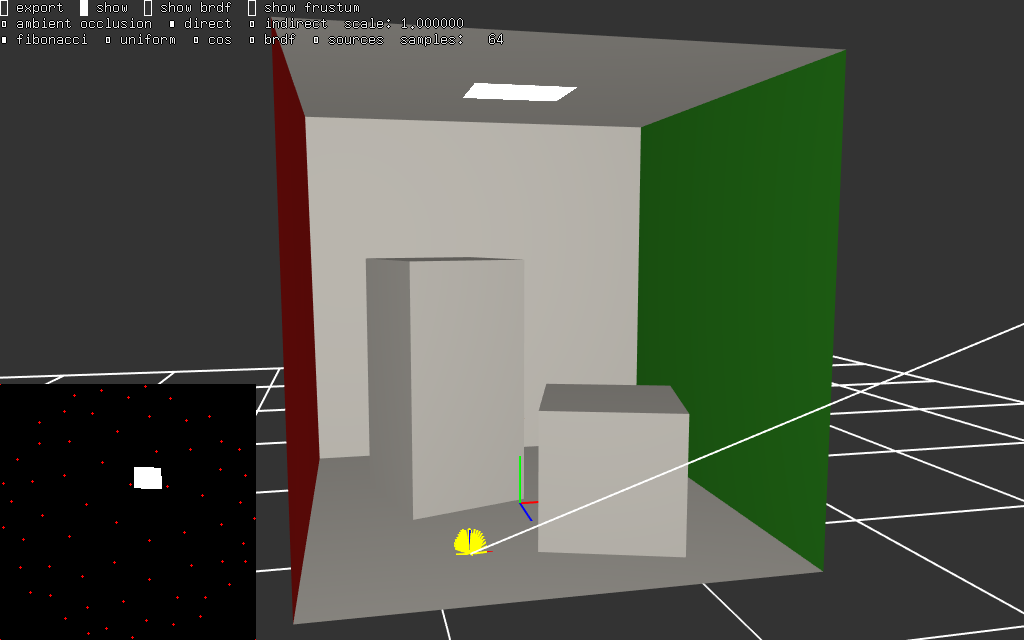 |  |
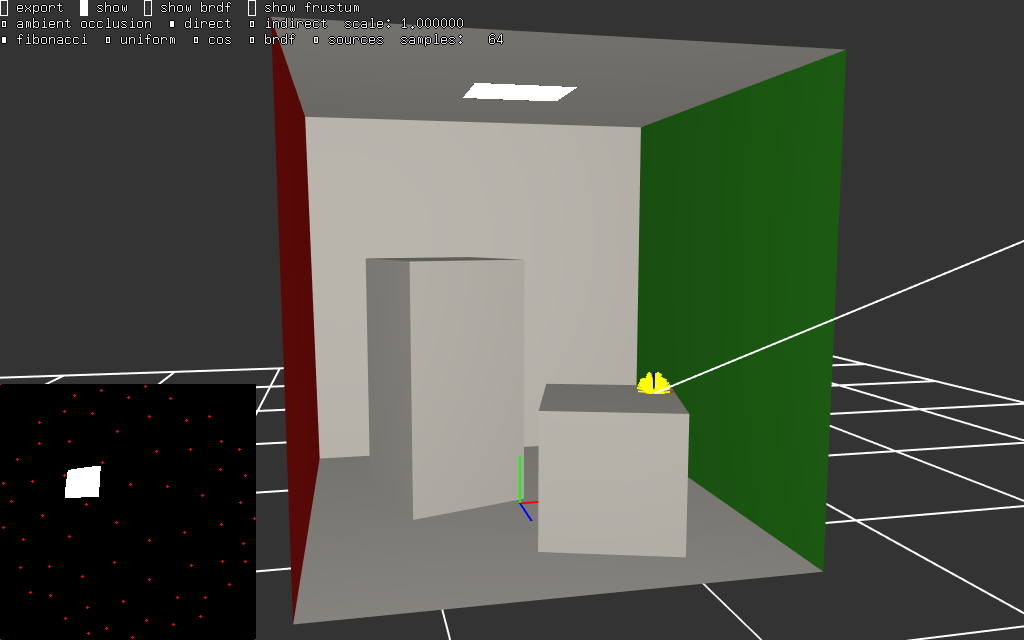
il y a beaucoup moins de directions qui voient la source... il faut zoomer un peu dans les images, mais les petits points rouges représentent 64 directions de la spirale de Fibonacci. en regardant attentivement, on peut constater que la source se trouve souvent entre les directions de la spirale. pour un point plus proche, la source apparaitra plus grande, ou plus petite pour un point plus loin, sur le sol par exemple.
mais dans tous les cas, on peut s'attendre à des résultats assez surprenants ?!
avec \( N= 1, 4, 16, 64 \)
 |  |
 |  |
et \( N= 256 \) :

et effectivement, même avec 256 directions, l'image reste pleine de défauts assez surprenants !
(oui bien sur, on peut utiliser quelques milliers de directions et une spirale orientée différement pour chaque point de calcul, mais cette première méthode est quand même assez peu adaptée au problème...)
bilan
il va falloir être un peu plus malin pour calculer une image correcte (et en temps raisonnable), bien que cette scène intérieure soit particulièrement simple...
la suite, comment utiliser les probas pour estimer l'équation de rendu de manière plus souple et plus robuste... cf intégration numérique et Monte Carlo