La lumière est émise par une source (de lumière ...), se propage dans la scène, rebondit sur un objet, se propage de nouveau et finit par arriver sur la camera. La matière d'un objet influence comment la lumière se diffuse autour de lui (apres le rebond) et définit l'apparence de l'objet, son aspect : mat, brilliant, transparent, etc.
quelques exemples d'apparence :
 |  | |
 |  |  |
Les objets n'ont pas toujours une surface bien définie : comme les cheveux, la laine, la végétation, etc. Pour les autres, pas de problèmes pour décrire leur surface. Comme ces cas sont aussi plus simples à dessiner, on va se concentrer dessus.
Pour créer une image, un minimum réaliste, il faut simuler les différentes étapes de la propagation de la lumière et surtout définir comment calculer / simuler le "rebond" de la lumière sur (la surface d') un objet. Ce rebond est décrit par le modèle de la matière de l'objet qui s'appelle brdf (abbrégé français de fonction de reflexion bidirectionnelle, brdf c'est bien...).
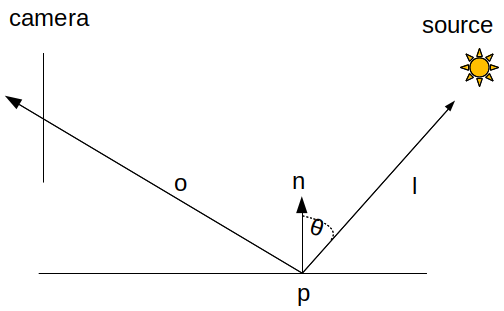
De manière générale, un modèle permet d'écrire que la lumière réfléchie dans une direction \( \vec{o} \) après le rebond est juste le produit de la lumière incidente \( L_i( \vec{l} ) \) et de la brdf, notée \( f_r() \) :
\[ f_r( \vec{o}, \vec{l} ) L_i( \vec{l} ) \]
la lumière incidente, notée \( L_i() \), arrive depuis la direction \( \vec{l} \), et \( f _r( \vec{o}, \vec{l} ) \) estime quelle fraction de cette énergie est réchéchie dans la direction \( \vec{o} \), vers l'observateur / la camera.
Bien sur, on pourrait scanner les matières et en déduire les valeurs de \( f_r() \), il existe quelques bases de données, mais les matières interressantes nécessitent trop de stockage (et trop de temps pour faire les mesures).
Du coup, il existe plusieurs modèles simplifiés. Par exemple : les matières mattes, les miroirs, les reflets, les matières composées de plusieurs couches (comme la peau, les objets vernis, certaines peintures) etc. que l'on peut calculer directement.
Il y a 2 modèles simples : le cas d'une reflexion parfaitement diffuse (une apparence matte) et une réflexion parfaitement spéculaire (un miroir). Ce sont les premiers travaux de Lambert, en 1760, et de Fresnel, en 1823, qui permettent de calculer le "rebond" de la lumière sur une surface plane / lisse.
Ces travaux sont complétés, dans les années 1960, et aboutissent aux modèles à microfacettes actuellement utilisés pour décrire la réflexion de la lumière sur une surface rugueuse qui est représentée comme une distribution de miroirs microscopiques.
 |  |  |
emission par la source de lumière
Si une source de lumière emet une certaine quantité de lumière, un flux exprimés en Watts, quelle quantité se propage jusqu'à un point de l'espace ? Sur l'ensemble des points se trouvant à une distance \( d \) de la source, on pourra mesurer la même valeur de flux. Le flux émis se répartit sur les \( 4 \pi d^2 \) points (l'aire de la sphère de rayon \( d \)), du coup, en un seul point, on ne mesure que \( \frac{1}{4 \pi d^2} \) du total emis par la source.
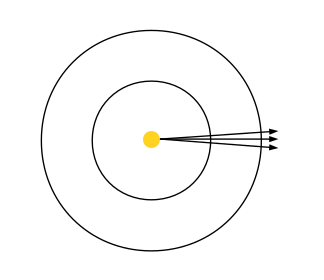
réflexion diffuse / Lambert
Si la surface sur laquelle on mesure la lumière incidente n'est pas orientée vers la source de lumière, le flux reçu se dépose sur plus de points, et chaque point ne mesure que \( \cos \theta \) du flux reçu.
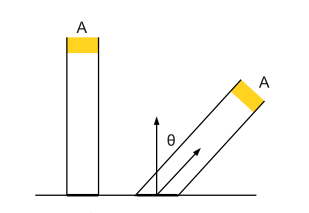
Pour résumer, le flux reçu par une surface est exprimé par unité d'aire de cette surface. Il dépend de la distance à la source (de son carré) et de l'orientation de la surface (du cosinus entre la normale et la direction vers la source).
L'apparence d'un objet parfaitement diffus est identique quelque soit la direction d'observation \( \vec{o} \), la matière réflechit la même quantité de lumière. On peut écrire :
\[ L_r( \vec{o} ) = k \cdot L_i( \vec{l} ) \cos \theta \]
\( L_r( \vec{o} ) \) est la quantité de lumière réfléchie dans la direction \( \vec{o} \). Le paramètre \( k \) compris entre 0 et 1, indique simplement que l'objet est très sombre ou très clair.
rappel : \( L_i( \vec{l} ) \) est la quantité de lumière incidente depuis la direction \( \vec{l} \), la direction vers la source.
Donc oui, le modèle de Lambert pour les réflexions / matières diffuses est une constante entre 0 et 1 :
\[ f_r( \vec{o}, \vec{l} ) = k \]
réflexion spéculaire et coefficients de Fresnel
Au contraire de la réflexion diffuse qui répartit la lumière incidente dans toutes les directions réflechies, la réflexion spéculaire ne réfléchit la lumière que dans une seule direction et ce sont les coefficients de Fresnel qui permettent de calculer quelle fraction de la lumière incidente se réfléchit dans cette direction. La quantité de lumière réfléchie dépend de l'angle d'incidence : ie de l'angle entre la normale à la surface et la direction de la lumière.
Toutes les matières ne se comportent pas de la même manière, elles sont caractérisées par un indice de réfraction \( \eta \), qui permet de déduire le coefficient de réflexion de Fresnel \( F() \) en fonction de la normale et de la direction de la lumière :
\begin{eqnarray*} F(\vec{n}, \vec{l}) & = & \frac{1}{2} \left( \frac{g - c}{g + c} \right)^2 \left( 1 + \left( \frac{c(g + c) -1}{c(g - c) +1} \right)^2 \right)\\ c & = & \cos \angle(\vec{n}, \vec{l}) = \cos \theta \\ g^2 & = & \eta^2 + c^2 -1 \end{eqnarray*}
Ces coefficients sont mesurés pour pas mal de matières : quelques exemples sur wikipedia et par exemple : 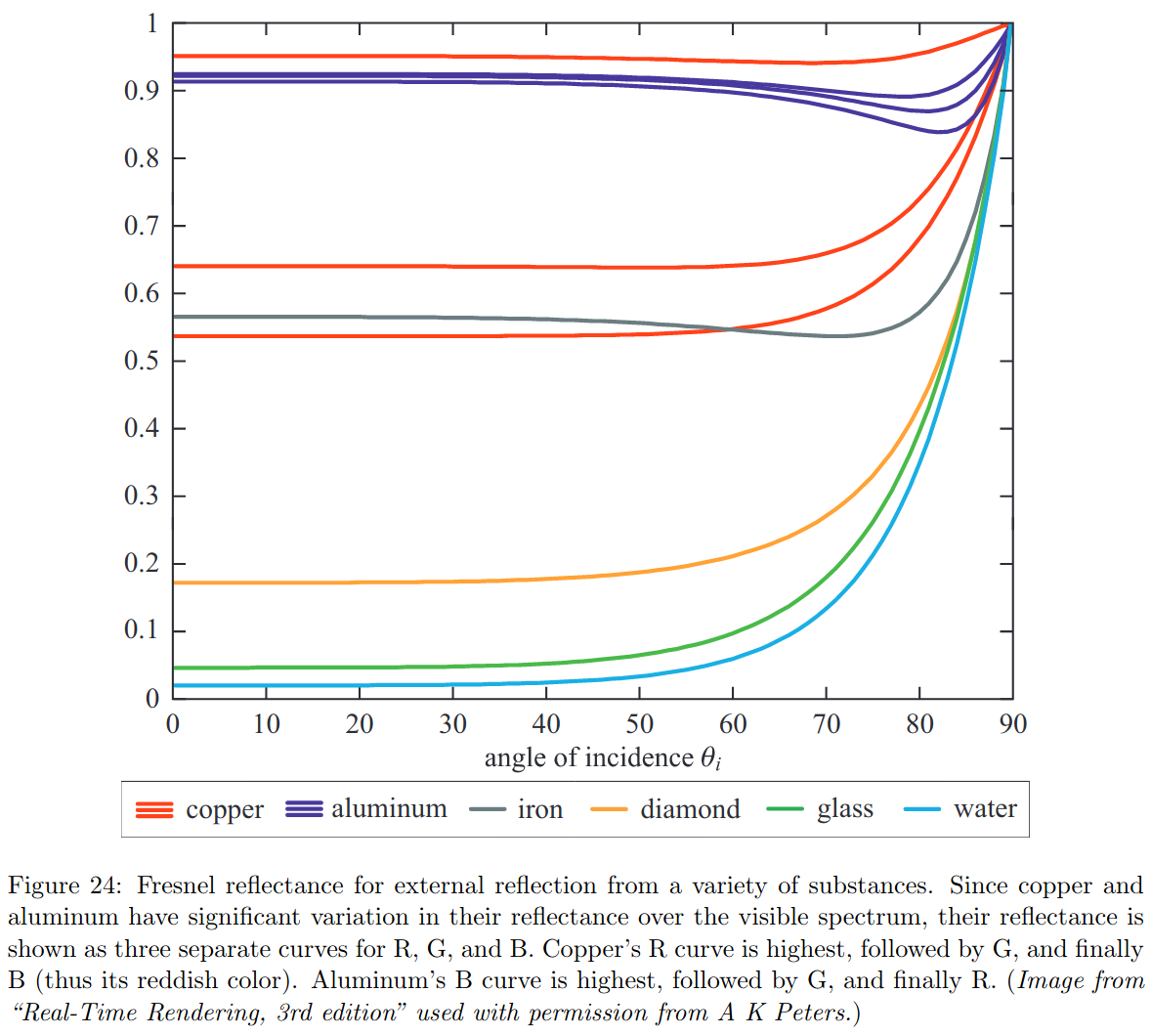
Dans l'exemple ci-dessus, une propriété des équations de Fresnel apparait : toutes les matières ont une réflexion de 1 à incidence rasante (la lumière arrive dans le plan tangent et \( \theta = 90° \)). Pour une incidence normale (la lumière arrive dans la direction de la normale et \( \theta = 0° \) ), l'équation se simplifie completement ( \( c = 1 \) dans ce cas), et on peut calculer le coefficient \( F(0)\) directement :
\[ F_0 = \left( \frac{\eta - 1}{\eta +1} \right)^2 \]
remarque : connaissant \( F_0 \), on peut aussi estimer un indice de réfraction pour l'incidente normale :
\[ \eta =\frac{1 + \sqrt{F_0}}{1 - \sqrt{F_0}} \]
Une approximation rapide à calculer qui utilise ces 2 propriétés est couramment utilisée, cf Schlick 94 :
\begin{eqnarray*} F(\vec{n}, \vec{l}) & = & F_0 + (1 - F_0) (1 - c)^5\\ c & = & \cos \angle(\vec{n}, \vec{l}) = \cos \theta \\ \end{eqnarray*}
Connaissant la direction miroir de \( \vec{l} \) par rapport à la normale de la surface on peut écrire la réflexion :
\[ L_r( \vec{m} ) = F(\vec{n}, \vec{l}) L_i( \vec{l} ) \]
et calculer la direction miroir : c'est la direction symétrique de \(\vec{l}\) par rapport à \(\vec{n}\) :
\[ \vec{m} = 2 (\vec{n} \cdot \vec{l}) \vec{n} - \vec{l} \]
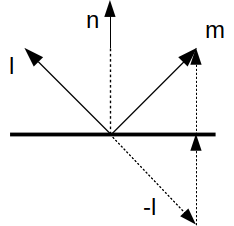
Par contre, pour formuler cette réflexion qui n'existe que pour la direction \( \vec{m} \), avec la fonction \( f_r() \), il faut prendre quelques précautions, pour s'assurer de renvoyer 0 pour les directions \( \vec{o} \) différentes de \( \vec{m} \) :
\begin{eqnarray*} f_r( \vec{o}, \vec{l} ) & = & 0 \mbox{ si } \vec{o} \not= \vec{m}\\ & = & \frac{ F(\vec{n}, \vec{l}) }{ \cos \theta } \mbox{ si } \vec{o} = \vec{m}\\ \end{eqnarray*}
remarque : oui, j'ai grossièrement simplifié tout ca... les équations de Fresnel sont nettement plus complètes que le cas particulier présenté au dessus (qui est valide pour les matières non métalliques et une lumière non polarisée...)
réflexion diffuse, réflexion spéculaire ? pourquoi ?
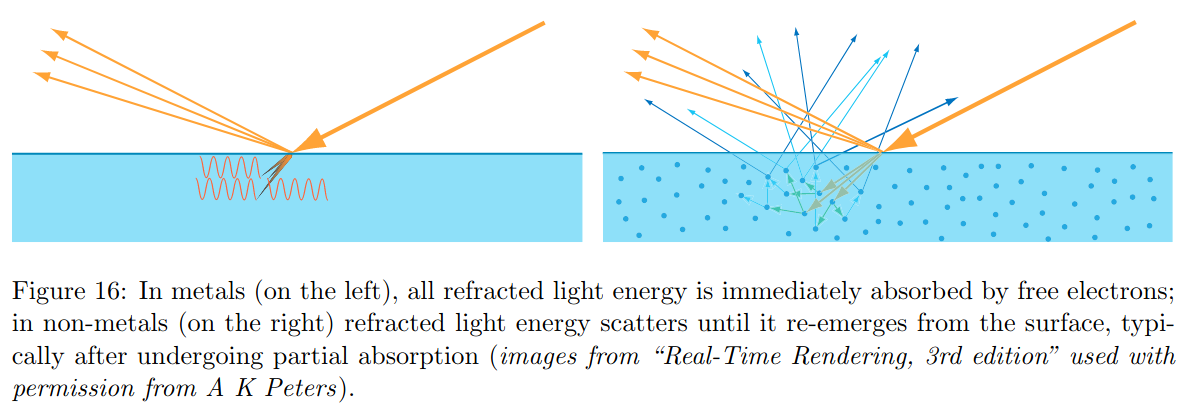
Les équations de Fresnel permettent de prédire le comportement de la lumière lorsqu'elle "rebondit" sur la surface d'un objet, mais selon la matière, il se passe des "choses" différentes. Il y a deux types de coefficients de Fresnel, ceux qui sont réels et ceux qui sont complexes (avec une partie imaginaire). Seuls les métaux ont des coefficients avec une partie imaginaire, toutes les autres matières (les diélectriques) n'ont que des coefficients réels.
et alors ? les métaux se comportent différemment, la couleur du reflet (de la lumière réfléchie) permet d'identifier le métal, alors que pour les autres matières la couleur du reflet est neutre.
La lumière rebondit à la surface de l'objet dans la direction miroir, et selon cas, elle se diffuse aussi dans la matière, "sous" la surface et ressort de la matière dans toutes les directions. Et globablement les métaux n'ont qu'une réflexion de surface, alors que les autres matières diffusent aussi la lumière sous la surface...
Et les termes spéculaire et diffus désignent ces deux comportements : spéculaire correspond à la réflexion en surface alors que diffus correspond à la propagation de la lumière dans la matière, sous la surface. Et cette séparation en deux termes se retrouve dans tous les modèles de matières.
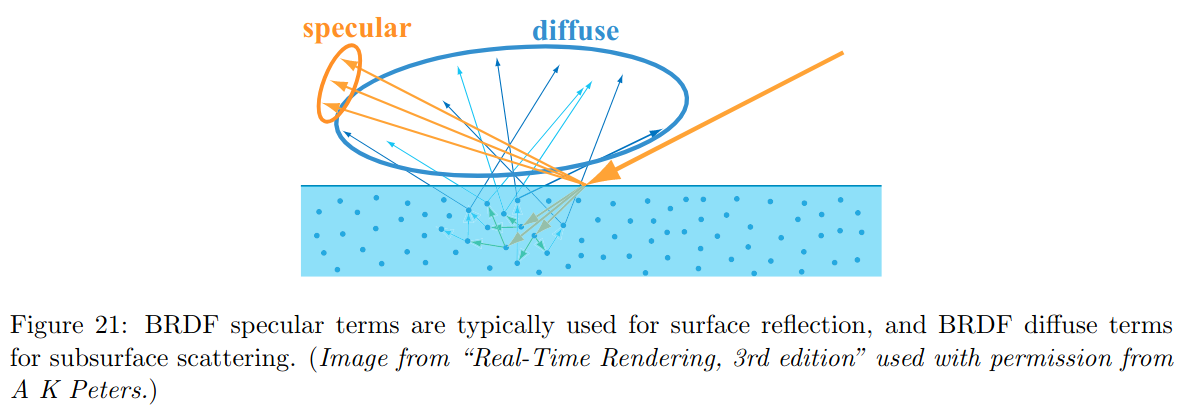
pour les curieux : les figures précédentes sont tirées de "Background: Physics and Math of Shading" N. Hoffman, 2012 qui reprend en details plusieurs phénomènes. Des informations plus détaillées sur les indices de réfraction complexes des métaux et les coefficients de Fresnel associés sont décrits dans le chapitre 8 de PBRT.
transmission ?
Ces équations représentent la quantité de lumière réfléchie par une surface lisse, mais comme mentionné juste au dessus, une partie de la lumière est aussi transmise sous la surface. Et de manière générale, tout ce qui n'est pas réfléchit au dessus de la surface est transmit sous la surface... Les équations de Fresnel définissent aussi :
\[ T(\vec{n}, \vec{l}) = 1 - F(\vec{n}, \vec{l}) \]
en pratique
La formulation un peu bizarre (avec la division par \( \cos \theta \)) dans le cas de reflexion spéculaire permet de formuler la lumière réfléchie de la même manière que le cas diffus :
\[ L_r( \vec{o} ) = f_r( \vec{o}, \vec{l} ) \cdot L_i( \vec{l} ) \cos \theta \]
c'est la fonction de reflexion, la brdf qui change en fonction des matières, pas son utilisation.
Pour calculer la couleur d'un pixel de l'image, il faut calculer la couleur de la lumière réflechie par le point de l'objet visible à travers le pixel : c'est à dire \( L_r( \vec{o} ) \). il faut aussi connaitre la position de la camera \( c \), la position du point \( p \), la normale de la surface à cette position \( \vec{n} \), la position de la source de lumière \( s \), son emission \( L_e \), et, enfin les paramètres de la matière :
- soit la constante \( k \) et une couleur pour les reflexions diffuses,
- soit 3 indices de réfraction \( \eta \) ou \( F_0 \) la couleur du reflet métallique pour les réflexions spéculaires.
Ces informations permettent d'évaluer tous les termes et de finir les calculs :
- \( \vec{o} = c - p \),
- \( \vec{l} = s - p \)
- \( L_i( \vec{l} )= L_e \)
Par contre, il y a une information que l'on ne connait pas directment avec une api3d classique : quelle est la lumière incidente pour les directions qui ne correspondent pas à une source de lumière ?? du coup, il est difficile de dessiner un miroir : puisque la couleur d'un pixel d'un miroir dépend de la couleur de l'objet dans la direction miroir \( \vec{m} \). La solution classique est d'utiliser du lancer de rayon pour traiter ce cas, ou d'utiliser une approximation comme les cubemaps, par exemple...
Dernier détail, d'ou vient la couleur ?? La physique décrit la réflexion de la lumière pour une seule longueur d'onde, pas pour l'ensemble du domaine visible que nos yeux percoivent. Dans le cas d'une matière diffuse, c'est la valeur du paramètre \( k \) qui change en fonction de la longueur d'onde et donne une couleur à un objet éclairé. Mais la couleur n'est qu'une perception du cerveau, elle n'existe pas dans la physique de la réflexion de la lumière. Et surtout, une matière n'a pas de couleur... par contre, un objet éclairé peut être observé et donc possède une couleur. Tout ça pour dire, que quand on dit qu'un objet est rouge, cela sous entend qu'il apparait de cette couleur lorsqu'il est éclairé normalement, par le soleil...
Du coup, pour simplifier les calculs, ont fait couramment une grosse approximation : la réflexion n'est évaluée que pour une longueur d'onde (qu'on suppose au milieu du domaine visible) et cette valeur est multipliée par la "couleur de base" la matière. Par exemple pour un objet rouge, représenté par \( rouge_{RGB} \), on aura :
\[ L_r( \vec{o} )_{RGB} = rouge_{RGB} \cdot f_r( \vec{o}, \vec{l} ) \cdot L_e \]
si on souhaite utiliser une source de "couleur", il est aussi possible d'utiliser \( L_{e_{RGB}} \). Mais attention il est frequent d'obtenir du noir, par exemple : une source rouge qui éclaire un objet bleu. Alors que si l'on avait fait les calculs pour chaque longueur d'onde, on aurait bien trouvé une "couleur" réfléchie...
Ces deux comportements permettent de représenter des matières parfaitement diffuses (comme du platre, par exemple) ou parfaitement spéculaires, comme un miroir parfaitement lisse, mais la plupart des objets n'ont pas une surface parfaitement lisse, il va donc falloir cogiter un peu plus.
La suite, la quête des reflets (sur des surfaces rugueuses / pas parfaitement lisses) : lumière et reflets
Puis, comment écrire des shaders pour faire ces calculs : shader et brdf.
Résumé du fonctionnement des shaders : shaders et GLSL.