on vient de voir dans synthèse réaliste et intégration numérique : l'équation de rendu que l'on a besoin d'estimer l'intégrale d'une fonction pour calculer la lumière réfléchie par un point de la scène. et qu'une méthode assez proche de l'intégration par rectangles n'est pas tout à fait adaptée au problème... quelles sont les autres solutions ?
on peut utiliser une relation issue des probas : on peut estimer l'espérance d'une variable aléatoire \( x \) :
\[ E(x) = \int x \, p(x) \, dx \approx \frac{1}{N} \sum_i^N x_i \]
ainsi que l'espérance d'une fonction de cette variable aléatoire :
\[ E(f(x)) = \int f(x) \, p(x) \, dx \approx \frac{1}{N} \sum_i^N f(x_i) \]
mais on a aussi besoin de connaitre la densité de probabilité de la variable aléatoire, \( p(x) \).
et alors ? comment peut-on utiliser cette définition pour estimer une intégrale ? par exemple :
\[ I = \int f(x)\, dx \]
il suffit de se rendre compte que \( \frac{f(x)}{p(x)}\) est aussi une fonction de \( x \) et que l'on peut exploiter le résultat précédent :
\[ E\left(\frac{f(x)}{p(x)}\right) = \int \frac{f(x)}{p(x)} \, p(x) \, dx = \int f(x) \, dx = I \approx \frac{1}{N} \sum_i^N \frac{f(x_i)}{p(x_i)} \]
c'est l'essentiel de la méthode Monte Carlo pour estimer une intégrale...
euh ? ça marche vraiment ?
on va comparer l'intégration par rectangles (cf wikipedia pour un résumé de la méthode) et l'intégration Monte Carlo d'une fonction simple en 1d :
\[ \int_{a=\, 0}^{b= \, 90°} \cos x \, dx \]

en utilisant les rectangles, on découpe le domaine d'intégration [a .. b] en \( N \) intervalles de même longueur \( \frac{1}{N} (b - a) \) :

la hauteur du rectangle est la valeur de la fonction et on peut écrire l'approximation :
\[ \int_a^b \cos x \, dx \approx \frac{1}{N} \sum_i^N (b-a) \, \cos x_i\\ \mbox{avec }a = 0 \mbox{ et }b= 90° \]
et avec Monte Carlo, on choisit aléatoirement des points dans l'intervalle [a .. b] :

on évalue aussi la fonction pour chaque point et on peut écrire l'estimateur Monte Carlo :
\[ \int_a^b \cos x \, dx = E(f/p) \approx \frac{1}{N} \sum_i^N \frac{\cos x_i}{p(x_i)} \]
et c'est quoi \( p(x_i) \) ? choisir un point aléatoirement dans un intervalle [a .. b] peut s'écrire \( p(x)= \frac{1}{b-a}\), ou de manière un peu plus lisible, choisir 1 point sur la longueur de l'intervalle [a .. b], et on peut re-écrire l'estimateur sous une forme très proche des rectangles :
\[ \int_a^b \cos x \, dx = E(f/p) \approx \frac{1}{N} \sum_i^N \frac{\cos x_i}{p(x_i)} = \frac{1}{N} \sum_i^N (b-a) \cos x_i \mbox{ avec }p(x_i)= \frac{1}{b-a} \]
alors ? c'est la même chose ? pas tout à fait, pour l'intégration par rectangles les points \( x_i \) sont disposés régulièrement entre a et b, pour l'estimateur Monte Carlo ils sont choisit aléatoirement... dans les 2 cas, on fait presque la même chose, on calcule les positions \( x_i \), on évalue la fonction \( f(x_i) \) et on calcule une moyenne (pondérée)...
le code est plutot direct :
et ça marche ? voila quelques résultats pour \( N \) variant de 1 à 1M. pour chaque nombre de points \( x_i \), le graphique montre aussi que l'on obtient des résultats différents à chaque exécution.

et on observe que plus le nombre de points utilisé pour estimer l'intégrale augmente, plus les différentes estimations sont stables, proches... l'estimation est plus précise avec plus de points... on dit que l'estimateur converge. pour un nombre infini de points, l'estimateur est exact... mais bien sur, on a rarement le temps de faire une infinité de calculs, il reste donc toujours une imprécision dans le résultat...
résumé
on vient de voir rapidement à quoi ressemble un estimateur Monte Carlo, le principe est le même quelque soit la fonction et le domaine d'intégration (un intervalle 1d, un carre 2d, une hemisphère de directions, etc). on part de la fomulation de l'intégrale à évaluer :
\[ I = \int f(x) \, dx \]
et on peut écrire l'estimateur :
\[ I \approx \frac{1}{N} \sum_i^N \frac{f(x_i)}{p(x_i)} \]
mais pour écrire ça, on a remplacé la variable d'intégration par une variable aléatoire. il faut pouvoir faire 2 choses avec cette variable aléatoire : évaluer sa densité de probabilité, \( p \), et savoir générer des points \( x_i \), des réalisations, de cette variable aléatoire selon sa densité de probabilité...
densité de probabilité et variable aléatoire
une densité de probabilité \( p \) est une fonction qui décrit les valeurs que peut prendre une variable aléatoire \( x \) et à quel point ces valeurs sont 'probables', si \( p(x_i) \) est faible (par rapport aux autres valeurs de \( p(x) \)), \( x_i \) est une valeur peu probable de la variable aléatoire.
ou, peut être plus intuitivement, \( p(x) \) est l'histogramme d'une variable aléatoire discrète \( x \), comme le résultat d'un lancer de dé. Pour \( N \) lancers du dé, on observe chaque face plus ou moins de fois. si le dé est normal, chaque face devrait apparaitre le même nombre de fois (ou pas, si le dé est pipé...)
remarque : oui, il existe des variables aléatoires continues comme un point dans un intervalle ou un carre et des variables aléatoires discrètes comme les tirages d'un dé.
si la densité est constante, \( p(x) = k \), on dit que la densité est uniforme, toutes les valeurs sont probables...
dans l'exemple ci-dessus, ie \( \int_a^b \cos x \, dx \), on pourrait vouloir placer plus de points au début de l'intervalle [a .. b] et moins à la fin de l'intervalle, au lieu de placer le même nombre de points partout. on voudrait utiliser une densité de proba de la forme \( 1 -x \) par exemple, mais comme \( x \) ne varie pas entre 0 et 1 mais entre a et b, il faut plutot quelque chose comme \( \frac{b-x}{b-a}\), mais une densité de proba doit être normalisée (par définition) :
\[ \int p(x) \, dx= 1 \]
il faut faire le calcul pour vérifier : \( \int_a^b \frac{b-x}{b-a} dx= \frac{b-a}{2}\) et pas vraiment 1... mais il suffit de diviser par ce résultat pour normaliser et obtenir une densité de proba :
\[ p(x)= \frac{2}{b-a} \frac{b-x}{b-a} \]
comment savoir combien de points se trouvent sur la première moitiée de l'intervalle ?
il suffit d'intégrer la densité, ce qui nous donne par définition la probabilité d'obtenir un point dans un intervalle quelconque :
\[ Pr\{x \in [a, b] \} = \int_a^b p(x) \, dx = P(b) - P(a) \]
la fonction \( P(x) \) est la fonction de répartition de la variable aléatoire, ou la probabilité d'observer des valeurs de la variable aléatoire dans l'intervalle [a .. b]. pour une variable aléatoire discrète, \( P(x) \) correspond à l'histogramme cumulé.
pour chaque moitiée [a .. m] et [m .. b] de l'intervalle [a .. b] on peut écrire :
\[ \begin{eqnarray*} Pr\{x \in [a, m] \} &= & \int_a^m p(x) \, dx = P(m) - P(a)\\ Pr\{x \in [m, b] \} &= & \int_m^b p(x) \, dx = P(b) - P(m) \end{eqnarray*} \]
pour \( p(x)= \frac{1}{b - a} \), on obtient, sans surprise :
\[ \begin{eqnarray*} Pr\{x \in [a, m] \}&= & \frac{1}{2}\\ Pr\{x \in [m, b] \}&= & \frac{1}{2} \end{eqnarray*} \]
ie, autant de points dans chaque moitiée de l'intervalle.
pour la densité \( p(x)= \frac{2}{b-a} \frac{b-x}{b-a}\), il faut faire le calcul, mais le résultat n'est pas non plus très surprenant :
\[ \begin{eqnarray*} Pr\{x \in [a, m] \}&= & \frac{3}{4}\\ Pr\{x \in [m, b] \}&= & \frac{1}{4} \end{eqnarray*} \]
ie on place 3 fois plus de points dans la 1ère moitiée que dans la seconde...
ce qu'il faut retenir : une variable aléatoire, ou plutot les valeurs possibles de la variable, sont décrites par 2 fonctions : la densité de probabilité \( p(x) \) et la fonction de répartition \( P(x) \) (qui est définie à partir de la densité). si la densité de proba est importante pour certaines valeurs, ces valeurs seront plus 'probables' ou plus souvent observées lors de \( N \) réalisations / tirages.
générer un point avec une densité de probabilité...
il manque une dernière étape pour estimer l'intégrale d'une fonction avec un estimateur Monte Carlo...
comment générer les points en fonction de p(x) ?
on sait choisir des points uniformément sur un intervalle [a .. b] avec une densité constante en utilisant un générateur de nombre pseudo-aléatoire standard qui permet d'obtenir des nombres aléatoires entre 0 et 1. il suffit d'étirer et de déplacer l'intervalle [0 .. 1] vers l'intervalle [a .. b]
voila 1000 points générés de cette manière. chaque point est dessiné sur une ligne différente, sinon on aurait juste une seule ligne, vu qu'il y a des points dans tout l'intervalle...

mais si la densité n'est pas constante ? comme dans l'exemple au dessus, ie \( p(x)= \frac{2}{b-a} \frac{b-x}{b-a}\) ?
on va commencer par un cas plus simple en 2 étapes :
- choisir dans quelle moitiée de l'intervalle [a .. b] placer un point, soit [a .. m] soit [m .. b]
- et ensuite choisir le point dans l'intervalle sélectionné, avec une densité uniforme, comme on vient de le faire pour [a .. b].
comment choisir un intervalle ? une solution simple serait de choisir l'indice de l'intervalle aléatoirement, ie tirer un nombre aléatoire entre 1 et 2, puis de placer un point uniformement dans cet intervalle. mais bien sur, c'est la même chose que le choix uniforme, chaque intervalle va être sélectionné le même nombre de fois... cette solution ne permet pas de choisir un intervalle plus souvent qu'un autre.
on voudrait choisir le 1er intervalle 3 fois plus souvent que l'autre intervalle, pour respecter les probabilités que l'on a calculé juste au dessus. mais il va falloir construire une variable aléatoire discrète avec les valeurs 1 et 2, ie les indices des intervalles et imposer que \( p(1) = \frac{3}{4}\) et \( p(2)= \frac{1}{4}\). connaissant un nombre aléatoire \( u \) entre 0 et 1, il est assez simple de retrouver à quel indice / intervalle il correspond.
il faut se rappeler la définition de la fonction de répartition des variables aléatoires discrètes :
\[ P(x_i)= \sum_{j=1}^{i} p(x_j) \]
soit pour les 2 intervalles :
- \( P(1)= p(1) = \frac{3}{4}\)
- \( P(2)= p(1) + p(2) = \frac{3}{4}+ \frac{1}{4}= 1\)
on sélectionne l'intervalle 1 si \( u \) vérifie \( u \leq P(1) \) ou l'intervalle 2 si \( u \leq P(2) \). ce qui s'écrit directement :
de manière générale, une valeur \( x_i \) est selectionnée si \( u \) vérifie :
\[ \begin{eqnarray*} P(x_{i-1}) & \leq & u \leq P(x_{i})\\ \sum_{j=1}^{i-1} p(x_j) & \leq & u \leq \sum_{j=1}^{i} p(x_j) \end{eqnarray*} \]
ou schématiquement, en partant de l'histogramme (ou de la densité de proba) :

on cherche à quelle valeur de la variable aléatoire correspond \( u \) en parcourant la fonction de répartition :

on peut maintenant finir le tirage / la génération d'un point, le plus difficile était de choisir les intervalles en respectant leur probabilité. une fois un intervalle sélectionné, il suffit de générer un point uniformément à l'intérieur :
mais dernière subtilité, les points sont distribués selon le produit de 2 densités, d'abord choisir un intervalle puis choisir un point dans cet intervalle :
- \( p(x)= \frac{3}{4} \frac{1}{(m-a)}\), si \( x \in [a, m]\),
- \( p(x)= \frac{1}{4} \frac{1}{(b-m)}\), si \( x \in [m, b]\).
voila à quoi ressemblent 1000 points :

on observe bien la séparation entre les 2 intervalles.
pour les curieux : on peut aussi vérifier le comportement de l'estimateur Monte Carlo en fonction de la manière de générer les points :
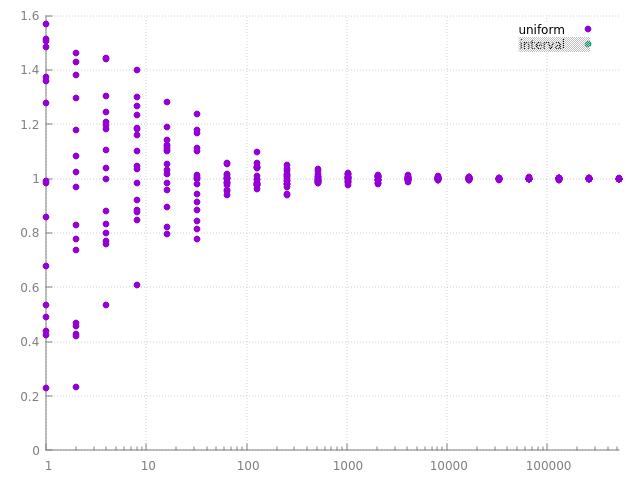 |  |
à gauche, avec les points générés aléatoirement et uniformément sur l'intervalle [a .. b], ie la 1ère solution, et à droite les points générés sur les 2 moitiés.
et alors ? de manière plus formelle, on vient d'inverser la fonction de répartition de la variable aléatoire, \( x_i= P^{-1}(u_i) \) et cette notion va permettre de faire la même chose avec des variables aléatoires continues. l'essentiel est de comprendre que l'on peut transformer un nombre uniforme entre 0 et 1 en valeur d'une variable aléatoire tout en respectant sa densité de proba...
générer des points avec une densité de proba continue...
on vient de voir que l'on peut générer des points assez facilement pour une variable aléatoire discrète en parcourant l'histogramme cumulé. on pourrait bien sur faire la même chose avec une variable continue, ie la découper en n morceaux, construire un histogramme, puis un histogramme cumulé et rechercher quelle valeur correspond à un nombre aléatoire uniforme entre 0 et 1... mais dans certains cas, on peut le faire directement, mais ca représente quelques calculs...
si on reprend l'idée d'utiliser \( p(x)= \frac{2}{b-a} \frac{b-x}{b-a}\), que faut-il faire ? l'idée est la même que pour une variable discrète, comme rappelé juste au-dessus : connaissant la densité de proba \( p(x) \), il faut l'intégrer pour obtenir la fonction de répartition \( P(x) \) et enfin l'inverser \( x= P^{-1}(u) \) pour générer un point \( x \) en fonction de \( u \).
1ère étape : calculer \( P(x) \), la fonction de répartition. par définition, on a :
\[ P(x)= \int_a^x p(t) \, dt = \int_a^x \frac{2}{b-a} \frac{b-t}{b-a} \, dt = \frac{(a-x) \, (x - 2b + a)}{(b-a)^2} \]
2ième étape : inversion, ie trouver l'expression de \( x \) en fonction de \( u \), on cherche les racines de \( P(x) - u = 0\) :
\[ \begin{eqnarray*} x_1& = & b - \sqrt{(1 - u)(b-a)^2}\\ x_2& = & b + \sqrt{(1 - u)(b-a)^2} \end{eqnarray*} \]
ah, comment ça on a plusieurs solutions ? vu que l'on ne s'interresse qu'aux valeurs de x dans l'intervalle [a .. b], on peut éliminer \( x_2 \) qui sera toujours plus grande que b (pourquoi ? on sait qu'une racine est toujours > 0, du coup b + racine est plus grand que b)
remarque : on peut utiliser une calculatrice en ligne pour faire les calculs, comme celle de wolfram par exemple.
et ça marche ?

on observe bien que les points sont distribués progressivement dans l'intervalle, au contraire de la solution précédente.
on peut également vérifier que l'on ne s'est pas trompé, en utilisant les points pour estimer l'intégrale. le code est sans surprise :
et voila le résultat pour \( N \) variant de 1 à 1M :
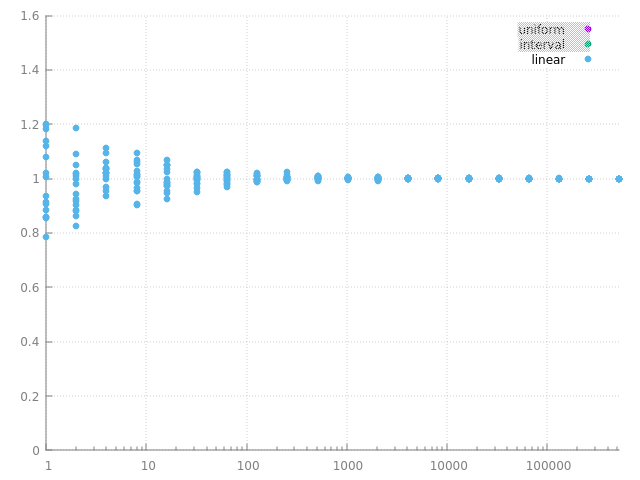
l'estimateur converge vers la même valeur qu'avec les points aléatoires uniformes ou ceux générés par intervalles, donc on ne s'est pas trompé, ni pour générer les points, ni pour évaluer leur densité de proba. par contre, on remarque que les estimations sont plus proches les unes des autres et que l'estimateur converge un peu plus vite...
pour terminer, il faut aussi remarquer qu'il y a assez peu de fonctions que l'on peut manipuler comme ça (intégration puis inversion) pour générer directement des points selon la fonction de répartition. et les calculs ne sont pas toujours simples, mais il existe des catalogues de fonctions / recettes de cuisine...
pour les malins : oui, tout ça ne sert à rien pour intégrer \( \cos \)... on sait faire le calcul directement, c'est un exemple 1d comme un autre. mais peut-on faire un truc plus interressant comme utiliser \( \cos \) pour densité de proba ? et peut-on également générer des points en fonction de cette densité ? quel serait l'impact sur la convergence de l'estimateur ?
bilan
on vient de voir plusieurs choses : la définition de l'intégration Monte Carlo, l'utilisation d'une variable aléatoire, la génération des points (ou des échantillons de manière générale, on va aussi générer des directions dans pas longtemps) en fonction de plusieurs densités de proba : uniforme, (semi-) discrète, et continue et que cette densité de proba des échantillons semble avoir un impact sur la convergence de l'estimateur.... mais avant de regarder cette propriété plus en détail, on va voir comment appliquer tout ça à l'équation de rendu... mais il va falloir manipuler des variables aléatoires 2d, pour générer des directions, par exemple (ou autre chose...).
la suite dans Monte Carlo et équation de rendu.