- ven. 02 février 2018
- Cours
- #ipython jupyter
%matplotlib inline
#%autosave 300
import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
from matplotlib import rcParams
rcParams['font.family'] = 'serif'
rcParams['font.size'] = 14
from IPython.core.display import HTML
from IPython.display import display
from matplotlib import animation
#from JSAnimation import IPython_display
css_file = 'style.css'
HTML(open(css_file, "r").read())
Programmation et Algorithme¶
Marc BUFFAT, dpt mécanique, Université Claude Bernard Lyon 1

Mise à disposition selon les termes de la Licence Creative Commons
Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 2.0 France.
Les bonnes pratiques de la programmation¶
les rêgles de programmation sous Python
import this
Un algorithme est une suite finie et non ambigüe d’opérations ou d’instructions permettant de résoudre un problème. Les algorithmes sont connus depuis l’antiquité (Euclide).
Le mot algorithme vient du nom du mathématicien perse du 9ième siècle (AJC)
- Abu Abdullah Muhammad ibn Musa al-Khwarizmi (photo).
L’algorithmique correspond à la phase préparatoire avant une quelconque programmation. Elle permet de décrire un problème sous une forme que l’on peut ensuite programmer sur un ordinateur et ceci dans un langage naturel, indépendant d’un langage de programmation.
algorithme numérique suite finie et non ambiguë d’opérations ou d’instructions sur des nombres permettant de résoudre un problème.
Et il n’est pas nécessaire d’avoir un ordinateur pour exécuter un algorithme (machine de Turing inventé en 1936 avant l’ordinateur)!
ordinateur = machine qui exécute (rapidement) des algorithmes
Algorithme itératif¶
Problème d’Euclide: pavage d’une piece¶
Soit une pièce rectangulaire de coté a et b (en cm) que l’on souhaites paver avec des petits carreaux carrés hxh.
Quelle est la taille maximum h des carreaux ?
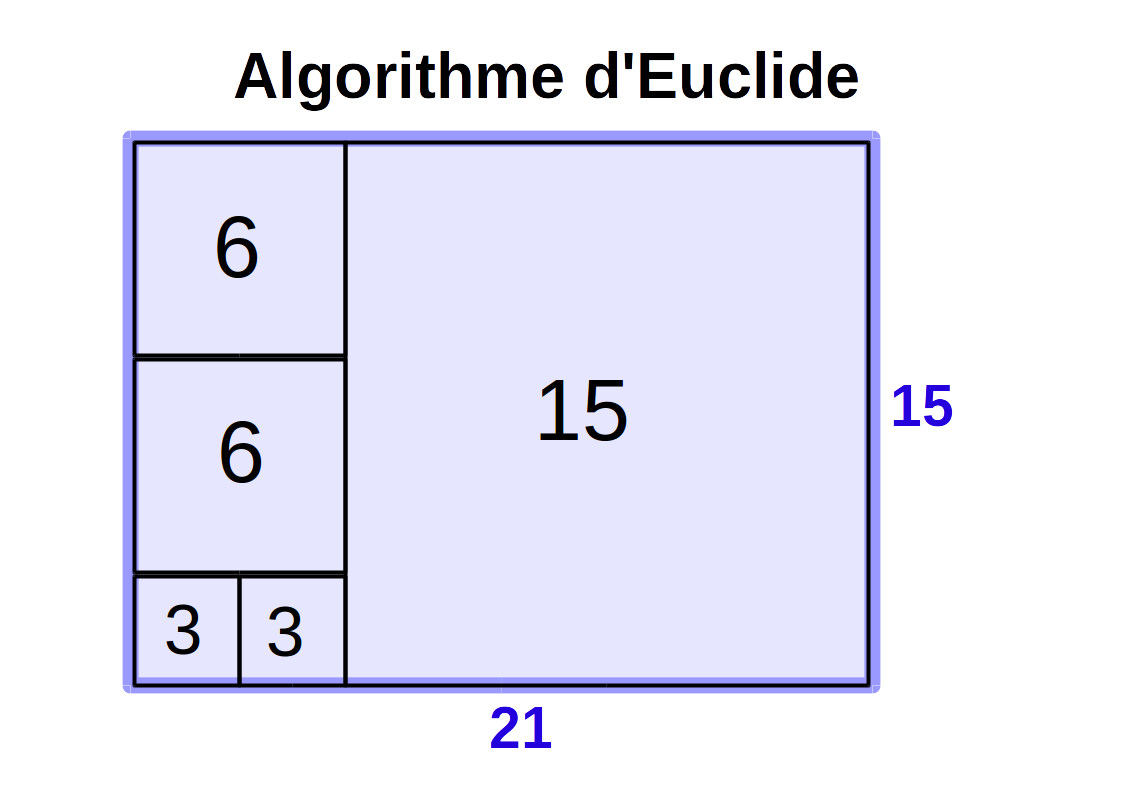
idée : découpage recursif / itératif de la pièce en carré
Algorithme PavageR(A,B)
détermine la taille maxi pour paver une piece de cotés AxB
# version recursive
si A > B alors
retour PavageR(A-B,A)
sinon si A < B alors
retour PavageR(A,B-A)
sinon
retour AAlgorithme Pavage(A,B)
détermine la taille maxi pour paver une piece de cotés AxB
# version itérative
tant que A # B faire
si A > B alors
A = A - B
sinon
B = B - A
fin tant que
# on a ici A=B donc
retour Adef PavageR(A,B):
'''version recursive du PGCD'''
print("PavageR : ",A,B)
if A > B :
return PavageR(A-B,B)
elif A < B :
return PavageR(B-A,A)
else :
return A
def Pavage(A,B):
'''version itérative du PGCD'''
while A != B :
print("Pavage : ",A,B)
if A > B :
A = A - B
else :
B = B - A
return A
PavageR(15,21)
Pavage(15,21)
Traduction en Python¶
def PavageR(a,b):
#print("PavageR:",a,b)
if a>b:
return PavageR(a-b,b)
elif a<b:
return PavageR(a,b-a)
else:
return a
def Pavage(a,b):
while a != b :
#print("Pavage:",a,b)
if a > b :
a = a - b
else :
b = b - a
return a
validation¶
print(Pavage(15,21))
print(PavageR(15,21))
print(Pavage(15,15))
print(PavageR(15,15))
n1=np.random.randint(10000)
n2=np.random.randint(10000)
%timeit Pavage(n1,n2)
%timeit PavageR(n1,n2)
variables globales et locales¶
attention: les arguments et les variables d'une fonction sont locales
def ma_fonction(a):
"""a et x locales"""
a=a-1
x=a+2
print("@a dans f=",id(a),a)
print("@x dans f=",id(x),x)
return
# programme principal
# a global
a=5
print("@a global =",id(a),a)
ma_fonction(a)
print("@a global=",id(a),a)
Calcul d’une série¶
Formulation mathématique: calcul de la somme d’une série¶
$$ S_N = x - \frac{x^2}{2} + \frac{x^3}{3} + .. = \sum_{i=1}^n (-1)^{i+1} x^i/i $$Solutions algorithmiques¶
1ere solution
Algorithme Serie1(x,n)
somme = 0
pour i de 1 a n
somme=somme + (-1)^(i+1)*x^i/i
retour somme
2nde solution (optimisée)
Algorithme Serie(x,n)
somme = 0
coeff = x
pour i de 1 a n
somme = somme + coef/i
coef = -coef*x
retour sommedef Serie(x,n):
'''calcul des n premiers termes de la série'''
somme = 0.
for i in range(1,n+1):
somme = somme + (-1)**(i+1)*(x**i)/i
return somme
def SerieO(x,n):
'''version optimisée'''
somme = 0.0
coeff = -1.0
for i in range(1,n+1):
coeff = - coeff*x
somme = somme + coeff/i
return somme
x=0.1
print(Serie(x,100),SerieO(x,100),np.log(1+x))
# algorithme en Python
from numpy import log
def serie1(x,n):
""" calcul de la somme de n termes de la serie x-x^2/2+x^3/3- """
somme=0.0
for i in range(1,n+1):
somme = somme + (-1)**(i+1)*x**i/i
return somme
# algorithme en Python (version optimisé)
from numpy import log
def serie(x,n):
""" calcul de la somme de n termes de la serie x-x^2/2+x^3/3- """
coef=x
somme=0.0
for i in range(1,n+1):
somme = somme + coef/i
coef = -coef*x
return somme
# utilisation et validation
x=0.2
n=10
print("Calcul de la serie pour x=",x," et n=",n)
print("somme1 = ",serie1(x,n))
print("somme = ",serie(x,n))
print("log(1+x) = ", log(1+x))
err = serie(x,n) - log(1+x)
print("erreur: ",err)
Efficacité: temps d’execution¶
utilisation de timeit pour calculer le temps d’exécution
ATTENTION l'important est une implémentation correcte et validée d'un lagorithme. La phase d'optimisation n'interviens qu'ensuite si nécéssaire!!!
%timeit serie1(x,10000)
%timeit serie(x,10000)



