trajectoire.mws

Trajectoire dans le plan

On se propose d'étudier la trajectoire d'un point P (x(t),y(t)) se déplacant sur une courbe  y=f(x)

Initialisation

> restart:with(plots): with(plottools): with(linalg):

Warning, the name changecoords has been redefined

Warning, the name arrow has been redefined

Warning, the protected names norm and trace have been redefined and unprotected

Etude de la courbe y=f(x)

> f:=x->x^4;x1:=-1;x2:=1;

f := proc (x) options operator, arrow; x^4 end proc

x1 := -1

x2 := 1

Tracé

> plot(f(x),x=x1..x2,thickness=3);

[Plot]

Dérivée: tangente

> diff(f(x),x);

4*x^3

> df:=x->diff(f(x),x);

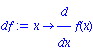
df := proc (x) options operator, arrow; diff(f(x), x) end proc

> df:=unapply(diff(f(x),x),x);

df := proc (x) options operator, arrow; 4*x^3 end proc

> df:=D(f);

df := proc (x) options operator, arrow; 4*x^3 end proc

Tracé

> plot(df(x),x=x1..x2,thickness=3);

[Plot]

Longueur: calcul de la longueur de la courbe

> dl:=sqrt(1+df(x)^2);

dl := (1+16*x^6)^(1/2)

> Int(dl,x=x1..x2)=int(dl,x=x1..x2);evalf(rhs(%));

Int((1+16*x^6)^(1/2), x = (-1 .. 1)) = -1/12*2^(1/3)*(-12*Pi^(1/2)*2^(2/3)*hypergeom([(-2)/3, (-1)/2], [1/3], (-1)/16)-2*Pi^2*3^(1/2)/(GAMMA(5/6)*GAMMA(2/3)))/Pi^(1/2)

3.200458856

Outils d'analyse avec Maple

> with(Student[Calculus1]):

> CurveAnalysisTutor(f(x),x=x1..x2);

> ArcLengthTutor(f(x),x=x1..x2);

Trajectoires d'un point se déplaçant à vitesse uniforme suivant x

> X:=t->t; Y:=unapply(f(X(t)),t); t1:=0; t2:=fsolve(X(t)=x2,t=0..10);

X := proc (t) options operator, arrow; t end proc

Y := proc (t) options operator, arrow; t^4 end proc

t1 := 0

t2 := 1.

Tracé

> plot([X(t),Y(t),t=t1..t2],thickness=2,scaling=CONSTRAINED);

[Plot]

Calcul de la Vitesse en différents points de la trajectoire

> DX:=D(X); DY:=D(Y);U:=[DX(t),DY(t)];

DX := 1

DY := proc (t) options operator, arrow; 4*t^3 end proc

U := [1, 4*t^3]

> N:=10; dt:=(t2-t1)/(N-1); Tp:=vector([seq(evalf(i*dt),i=0..N-1)]);

N := 10

dt := .1111111111

Tp := vector([0., .1111111111, .2222222222, .3333333333, .4444444444, .5555555555, .6666666666, .7777777777, .8888888888, .9999999999])

> Mx:=vector([seq(evalf(X(Tp[i])),i=1..N)]);My:=vector([seq(evalf(Y(Tp[i])),i=1..N)]);

Mx := vector([0., .1111111111, .2222222222, .3333333333, .4444444444, .5555555555, .6666666666, .7777777777, .8888888888, .9999999999])

My := vector([0., 0.1524157902e-3, 0.2438652643e-2, 0.1234567901e-1, 0.3901844230e-1, 0.9525986888e-1, .1975308641, .3659503123, .6242950767, .9999999996])

> Ux:=vector([seq(evalf(DX(Tp[i])),i=1..N)]);Uy:=vector([seq(evalf(DY(Tp[i])),i=1..N)]);

Ux := vector([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.])

Uy := vector([0., 0.5486968448e-2, 0.4389574760e-1, .1481481481, .3511659807, .6858710560, 1.185185185, 1.882030178, 2.809327846, 3.999999999])

Tracé de la vitesse

> P1:=plots[arrow]({seq([[Mx[i],My[i]],[Ux[i],Uy[i]]],i=1..N)},shape=arrow,color=red,thickness=3,length=[0.05,relative]):P2:=plot([X(t),Y(t),t=t1..t2],thickness=1,color=blue):
display({P2,P1});

[Plot]

Abscisse curviligne

> ds:=unapply(simplify(sqrt(DX(t)^2+DY(t)^2)),t);
Int('ds'(t),t)=int(ds(t),t);

ds := proc (t) options operator, arrow; (1+16*t^6)^(1/2) end proc

Int(ds(t), t) = t*hypergeom([(-1)/2, 1/6], [7/6], -16*t^6)

> s:=unapply(int(ds(tau),tau=0..t),t); evalf(s(1));

s := proc (t) options operator, arrow; -1/24*2^(1/3)*(-12*Pi^(1/2)*t^4*2^(2/3)*hypergeom([(-2)/3, (-1)/2], [1/3], -1/16*1/t^6)-2*Pi^2*3^(1/2)/(GAMMA(5/6)*GAMMA(2/3)))/Pi^(1/2) end proc

1.600229428

> plot(evalf(s(t)),t=t1..t2,title="longueur de la trajectoire",thickness=2);

[Plot]

Repere de Frenet: vecteur T tangent et N normal

> T:=evalm(1/ds(t)*U); dT:=factor([diff(T[1],t),diff(T[2],t)]);
dTds:=factor(sqrt(dT[1]^2+dT[2]^2));
N:=(evalm(1/dTds*[dT[1],dT[2]]));

T := vector([1/(1+16*t^6)^(1/2), 4*t^3/(1+16*t^6)^(1/2)])

dT := [-48*t^5/(1+16*t^6)^(3/2), 12*t^2/(1+16*t^6)^(3/2)]

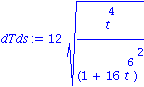
dTds := 12*(t^4/(1+16*t^6)^2)^(1/2)

N := vector([-4*t^5/((t^4/(1+16*t^6)^2)^(1/2)*(1+16*t^6)^(3/2)), t^2/((t^4/(1+16*t^6)^2)^(1/2)*(1+16*t^6)^(3/2))])

Acceleration et accelération normale

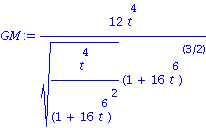
> D2X:=D(DX); D2Y:=D(DY); GM:=factor(D2X(t)*N[1]+D2Y(t)*N[2]);

D2X := 0

D2Y := proc (t) options operator, arrow; 12*t^2 end proc

GM := 12*t^4/((t^4/(1+16*t^6)^2)^(1/2)*(1+16*t^6)^(3/2))

Carre de la vitesse et courbure

> V2:=DX(t)^2+DY(t)^2;

V2 := 1+16*t^6

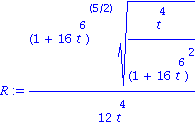
> R:=V2/GM;

R := (1+16*t^6)^(5/2)*(t^4/(1+16*t^6)^2)^(1/2)/(12*t^4)

Tracé de la courbure

> plot(1/R,t=t1..t2,discont=true,thickness=2);

[Plot]

Calcul en fonction de la dérivée seconde

> C:=diff(f(x),x$2)/(1+diff(f(x),x)^2)^(3/2);
plot(C,x=0..x2,thickness=2);

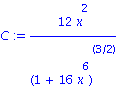
C := 12*x^2/(1+16*x^6)^(3/2)

[Plot]

Repere de Frenet en un point

> t0:=0.5; M0:=[X(t0),Y(t0)]; U0:=[DX(t0),DY(t0)];G0:=[D2X(t0),D2Y(t0)];
R0:=evalf(subs(t=t0,R));
T0:=evalf(subs(t=t0,evalm(T)));N0:=evalf(subs(t=t0,evalm(N)));

t0 := .5

M0 := [.5, 0.625e-1]

U0 := [1, .500]

G0 := [0, 3.00]

R0 := .4658474957

T0 := vector([.8944271908, .4472135952])

N0 := vector([-.4472135952, .8944271904])

Tracé du repere de Frenet

> P1:=plots[arrow]({[M0,N0],[M0,T0]},shape=arrow,color=pink,thickness=3,length=[0.5,relative],
scaling=CONSTRAINED):
P11:=plots[arrow]({[M0,U0],[M0,G0]},shape=arrow,color=red,thickness=2,length=[0.1,relative],
scaling=CONSTRAINED):
C0:=evalf(evalm(M0+R0*N0)):
C:=circle([C0[1],C0[2]],R0,color=green):MC:=point([C0[1],C0[2]],color=black,thickness=5):
P2:=plot([X(t),Y(t),t=t0-0.5..t0+0.5],color=blue):
display({P1,P11,C,MC,P2});

[Plot]

Relation entre courbure et dérivée

> DS:=sqrt(1+DF(x)^2);TX:=1/DS; TY:=DF(x)/DS;

DS := (1+DF(x)^2)^(1/2)

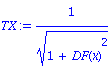
TX := 1/(1+DF(x)^2)^(1/2)

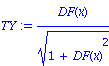
TY := DF(x)/(1+DF(x)^2)^(1/2)

> DTX:=diff(TX,x)/DS;
DTY:=simplify(diff(TY,x)/DS);

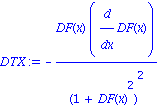
DTX := -DF(x)*diff(DF(x), x)/(1+DF(x)^2)^2

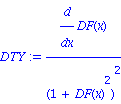
DTY := diff(DF(x), x)/(1+DF(x)^2)^2

> sqrt(simplify(DTX^2+DTY^2));

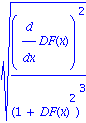
(diff(DF(x), x)^2/(1+DF(x)^2)^3)^(1/2)

> R:='R': 1/R=diff(F(x),x$2)/(1+diff(F(x),x)^2)^(3/2);

1/R = diff(F(x), `$`(x, 2))/(1+diff(F(x), x)^2)^(3/2)

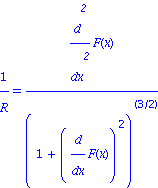
FIN!