TourMaple.ms
MAPLE V
Un outil de calcul symbolique pour Ingenieurs et Scientifique
par Marc BUFFAT , UFR de Mécanique, UCB Lyon I
INTRODUCTION
Maple V est un outil d'aide pour:
Le calcul numerique
Les traces mathematiques 2D et 3D
Le calcul algebrique ou symbolique
Le calcul differentiel et integral
La resolution d'equations differentielles
L'algebre lineaire
Maple V est un outil d'aide !!!
Il ne resoud pas les problemes a votre place (ce n'est pas une boite noire)
Maple V possede un langage pour entrer les commandes
et une aide en ligne (Help)
Un programme Maple doit commence par une remise a zero du moteur maple
| > |
# Ceci est un commentaire |
| > |
print(`Bonne nuit les petits`); |
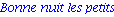
CALCUL NUMERIQUE
Calcul Numerique avec une arithmetique exacte

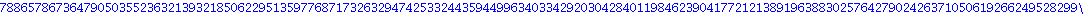
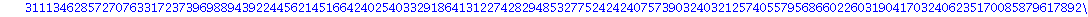

Factorisation du resultat % en nombres premiers
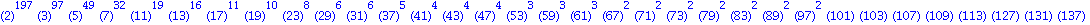

Verification

Calcul exacte avec des fractions et des puissances

Mais evaluation possible avec une precision quelconque

Autres Examples
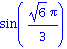
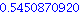
Maple V calcule des sommes et des produits finies ou infinies
| > |
Sum((1+i)/(1+i^4), i=1..10); |
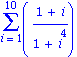

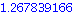
| > |
P:=Product(((i^2+3*i-11)/(i+3)), i=0..10); |
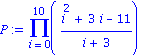
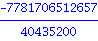
Calculs flottants
Maple V peut effectuer des calculs en flottants avec une precision quelconque
par example avec 50 chiffres

FONCTIONS MATHEMATIQUES
Maple V connait les nombres complexes (I=sqrt(-1))
Les fonctions mathematiques et les constantes
| > |
Pi; sin(Pi/2); cos(Pi/4); exp(log[10](10)); |
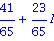


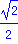

Evaluation de Pi avec 70 chiffres
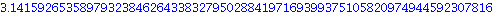
GRAPHIQUE
Warning, the name changecoords has been redefined
trace 2D
Trace de fonctions
| > |
plot(sin(x)/x,x=0..6*Pi,thickness=2,title="sin(x)/x"); |
![[Plot]](images/TourMaple_25.gif)
Trace de fonctions avec gestion des discontinuites
| > |
plot( tan(x), x=-2*Pi..2*Pi, -4..4, discont=true, title="Trace de Tan(x)");
|
![[Plot]](images/TourMaple_26.gif)
Trace de fonctions de 2 variables explicites ou implicites
| > |
plot3d(x*exp(-x^2-y^2), x=-2..2, y=-2..2,axes=BOXED, title=`Surface Plot`);
|
![[Plot]](images/TourMaple_27.gif)
Trace 3D
Trace 3D de la surface de Kuen
| > |
kuenx:= (u,v) -> 2*(cos(u) + u*sin(u))*sin(v)/(1 + (u*sin(v))^2);
kueny:= (u,v) -> 2*(sin(u) - u*cos(u))*sin(v)/(1 + (u*sin(v))^2);
kuenz:= (u,v) -> log(tan(v/2)) + 2*cos(v)/(1 + (u*sin(v))^2);
plot3d([kuenx,kueny,kuenz],-4..4,.01..Pi-.01,grid=[35,35],
orientation=[146,76],projection=0.8,
style=patch,ambientlight=[.9,.8,.9], title=`The Kuen Surface`); |
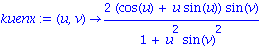
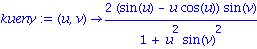
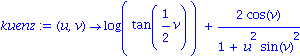
![[Plot]](images/TourMaple_31.gif)
Trace de fonctions implicites: super-ellipsoide x^10+y^10+z^10-1=0 .
| > |
implicitplot3d(x^10+y^10+z^10-1=0,x=-1..1,y=-1..1,z=-1..1,style=PATCHNOGRID,
title=`A Super-ellipsoid`); |
![[Plot]](images/TourMaple_32.gif)
Animation
Possibilite d'animations
| > |
animate( {x-x^3/t , sin(t*x)}, x=0..Pi/2, t=1..16); |
![[Plot]](images/TourMaple_33.gif)
CALCUL ALGEBRIQUE
expression mathématiques
Maple sait manipuler, simplifier, evaluer des expressions mathematiques
avec des variables (au sens mathematique)
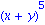
Que l'on peut developper
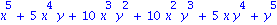
Et refactoriser
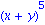
De meme il peut simplifier des expressions trigonometriques
| > |
cos(x)^5 + sin(x)^4 + 2*cos(x)^2 - 2*sin(x)^2 - cos(2*x);
simplify(%); |


Normaliser des fractions
| > |
(x^3-y^3)/(x^2+x-y-y^2); normal(%); |
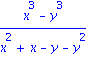
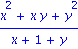
On peut definir des variables pour manipuler des expressions
| > |
my_expr := (41*x^2+x+1)^2*(2*x-1); |
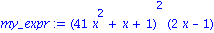
Puis la developper
| > |
my_result := expand(my_expr); |
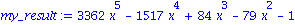
On peut convertir des expressions trigonometriques en notation exponentielle
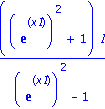
Définition de fonction
Maple V permet de definir ses propres fonctions avec l'operateur ->
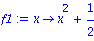
Et l'on peut obtenir des valeurs numeriques ou symboliques

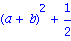
Pour des fonctions plus complexes, on peut utiliser des procedures
| > |
f2 := proc(x)
if x > 3 then x^2
else x-5
fi;
end; |
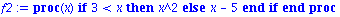
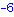
| > |
plot( f2, 0..6, title=`Fonction définie par morceaux`, axes=BOXED );
|
![[Plot]](images/TourMaple_50.gif)
RESOLUTION D'EQUATION et de SYSTEME D'EQUATIONS
Recherche des racines d'une equation
| > |
expr := x^3-1/2*x^2*a+13/3*x^2 = 13/6*x*a+10/3*x-5/3*a; |
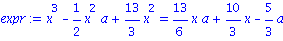
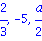
Resolution de systemes d'equations
| > |
eqn1 := x+2*y+3*z+4*t+5*u=41;
eqn2 := 5*x+5*y+4*z+3*t+2*u=20;
eqn3 := 3*y+4*z-8*t+2*u=125;
eqn4 := x+y+z+t+u=9;
eqn5 := 8*x+4*z+3*t+2*u=11; |
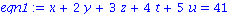
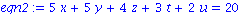
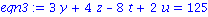

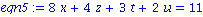
solution
| > |
s1 := solve({eqn1,eqn2,eqn3,eqn4,eqn5}, {x,y,z,t,u}); |
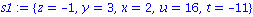
Resolution de problemes sous-contraints
| > |
s2 := solve({eqn||(1..3)}, {x,y,z}); |
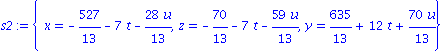
CALCUL DIFFERENTIEL ET INTEGRAL
Series
Developpement en series de fonctions
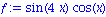
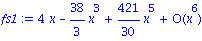
Que l'on peut comparer graphiquement
| > |
plot({f, convert(fs1,polynom)},x=-1..1, -2..2,
title=`sin(4x) cos(x) vs. Series`);
|
![[Plot]](images/TourMaple_62.gif)
En augmentant l'ordre de tronacture a 12
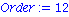
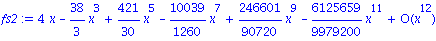
| > |
plot({f, convert(fs2,polynom)}, x=-1..1, -2..2,
title=`sin(4x) cos(x) vs. Series`);
|
![[Plot]](images/TourMaple_65.gif)
Calcul de limite
limite d'expression
| > |
f := (x^2-2*x+1)/(x^4+3*x^3-7*x^2+x+2); |
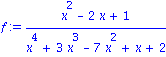

Meme a l'infini
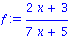

Limite a gauche
| > |
limit(tan(x), x=Pi/2, left); |

Et a droite
| > |
limit(tan(x), x=Pi/2, right); |

Derivees et primitives
calcul symbolique de derivees et de primitives
| > |
f := x*sin(a*x) + b*x^2; |
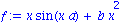
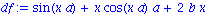
primitive
| > |
int(df,x); simplify(%); |
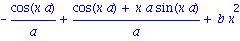
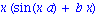
Calcul d'integrale definie
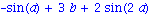
Exemple plus complexe ?
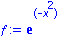

Un autre exemple
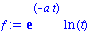
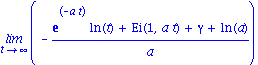
En precisant que le parametre a est positif, on peut simplifier
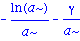
Pour eliminer l'hypothese sur a
integrales spéciales
Calcul d'integrales elliptiques avec les fonctions mathematiques speciales
| > |
f := 1/sqrt(2*t^4-3*t^2-2); |
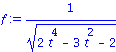
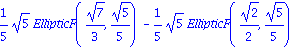
EQUATIONS DIFFERENTIELLES ou ODE
ODE
ODE du 2nd ordre
| > |
diff_eq1 := diff(y(t),t,t) + 5*diff(y(t),t) + 6*y(t) = 0; |
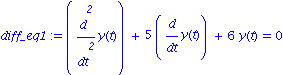
Conditions initiales en 0: y(0) et dy/dx(0):
| > |
init_con := y(0)=0, D(y)(0)=1; |
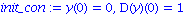
Resolution avec dsolve()
| > |
dsolve({diff_eq1,init_con},y(t)); |
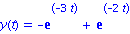
ODE du 4ieme ordre:
| > |
diff_eq2 := 10^6*diff(y(x),x,x,x,x) = Dirac(x-2) - Dirac(x-4); |
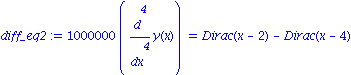
avec des C.L.
| > |
bound_con := y(0)=0, D(D(y))(0)=0, y(5)=0, D(D(y))(5)=0; |
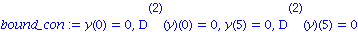
Resolution avec dsolve:
| > |
soln := dsolve({diff_eq2,bound_con},y(x)); |
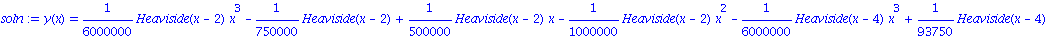

Puis trace
| > |
plot(rhs(soln),x=0..5, axes=BOXED, title=`Solution to a 4th Order BVP`); |
![[Plot]](images/TourMaple_91.gif)
Système d'ODE
Resolution de systemes d'ODE.
| > |
de_sys := diff(y(x),x,x)=z(x), diff(z(x),x,x)=y(x); |
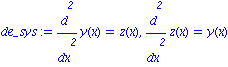
La solution est donnee en fonction de constantes d'integration _C1 ...
| > |
dsolve({de_sys}, {z(x),y(x)}); |
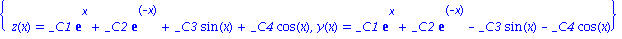
CALCUL MATRICIEL
Chargement de la librairie d'algebre lineaire
Warning, the protected names norm and trace have been redefined and unprotected
Matrice 3x3
| > |
M1 := array([[1/2,-1/3,2],[-5,14/3,9],[0,11,-5/6]]): M1;print(M1); |
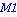
![matrix([[1/2, (-1)/3, 2], [-5, 14/3, 9], [0, 11, (-5)/6]])](images/TourMaple_95.gif)
Calcul de l'inverse
![matrix([[1852/2881, (-391)/2881, 222/2881], [75/2881, 15/5762, 261/2881], [990/2881, 99/2881, (-12)/2881]])](images/TourMaple_96.gif)
Matrice avec des coefficiants symboliques
| > |
M2 := array([[1/2,0,-2],[sin(theta),1,phi^2],[0,phi-1,3/4]]); |
![M2 := matrix([[1/2, 0, -2], [sin(theta), 1, phi^2], [0, phi-1, 3/4]])](images/TourMaple_97.gif)
Multiplication:
![M3 := matrix([[1/4-1/3*sin(theta), -7/3+2*phi, 1/2-phi^2/3], [-5/2+14/3*sin(theta), -13/3+9*phi, 67/4+14*phi^2/3], [11*sin(theta), 71/6-5*phi/6, -5/8+11*phi^2]])](images/TourMaple_98.gif)
Calcul du determinant
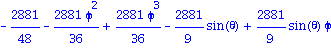
Des valeurs propres et des vecteurs propres ??
| > |
map(simplify,[eigenvals(M2)]); |








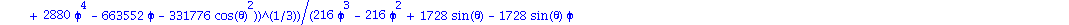















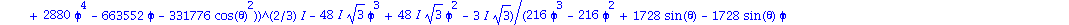














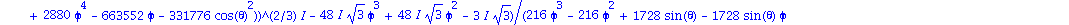



Que l'on peut evaluer
| > |
simplify(eval(subs(phi=0,theta=0,%))); |
![[1, 1/2, 3/4]](images/TourMaple_143.gif)
Vandermonde matrice pour les variables s, t, u, v, et w:
| > |
vandermonde([s,t,u,v,w]); |
![matrix([[1, s, s^2, s^3, s^4], [1, t, t^2, t^3, t^4], [1, u, u^2, u^3, u^4], [1, v, v^2, v^3, v^4], [1, w, w^2, w^3, w^4]])](images/TourMaple_144.gif)
PROGRAMMATION
Boucle
boucle: for var from debut by pas to fin do instr. end do;
| > |
s:=0:
for i from 1 by 2 to 100 do
s:=s+i
end do:
's'=s; |
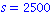
boucle tant que: while condition do instr. end do;
| > |
s:=0: i:=1:
while s<2500 do
s:=s+i; i:=i+2;
end do:
i; s; |
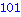
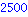
Sortie de boucle: break
Test logique
Test logique: if cond. then exp1 else exp2 end if;
comparaison: >, >=, <, <=, =, <>, and , or , not
| > |
if (a>b) then a else b end if; |
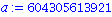

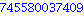
Procedure
Calcul du PGCD de nombres entiers a et b
| > |
PGCD:=proc(a,b)
local x1,x2;
x1:=a; x2:=b;
while (x1<>x2) do
if (x1>x2) then x1:=x1-x2 else x2:=x2-x1 end if;
end do;
return x1;
end proc; |
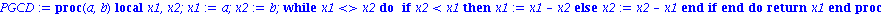
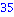
FIN
![]()
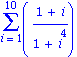
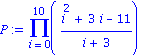
![[Plot]](images/TourMaple_25.gif)
![[Plot]](images/TourMaple_26.gif)
![[Plot]](images/TourMaple_27.gif)
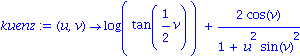
![[Plot]](images/TourMaple_31.gif)
![[Plot]](images/TourMaple_32.gif)
![[Plot]](images/TourMaple_33.gif)
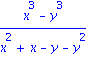
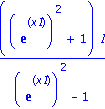
![[Plot]](images/TourMaple_50.gif)
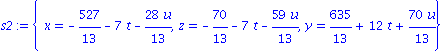
![[Plot]](images/TourMaple_62.gif)
![[Plot]](images/TourMaple_65.gif)
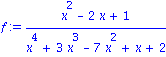
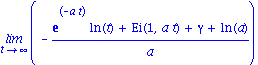
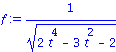
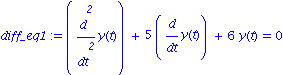
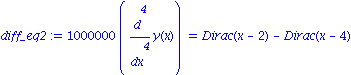
![[Plot]](images/TourMaple_91.gif)
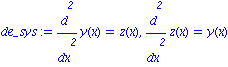
![matrix([[1/2, (-1)/3, 2], [-5, 14/3, 9], [0, 11, (-5)/6]])](images/TourMaple_95.gif)
![matrix([[1852/2881, (-391)/2881, 222/2881], [75/2881, 15/5762, 261/2881], [990/2881, 99/2881, (-12)/2881]])](images/TourMaple_96.gif)
![M2 := matrix([[1/2, 0, -2], [sin(theta), 1, phi^2], [0, phi-1, 3/4]])](images/TourMaple_97.gif)
![M3 := matrix([[1/4-1/3*sin(theta), -7/3+2*phi, 1/2-phi^2/3], [-5/2+14/3*sin(theta), -13/3+9*phi, 67/4+14*phi^2/3], [11*sin(theta), 71/6-5*phi/6, -5/8+11*phi^2]])](images/TourMaple_98.gif)
![matrix([[1, s, s^2, s^3, s^4], [1, t, t^2, t^3, t^4], [1, u, u^2, u^3, u^4], [1, v, v^2, v^3, v^4], [1, w, w^2, w^3, w^4]])](images/TourMaple_144.gif)