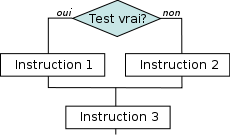
si (expression vrai) alors
execute intruction(s) 1
sinon
execute intruction(s) 2
fin si
execute instruction(s) 3
|
if expression :
intruction1
else : intruction2
instruction3
</code></td></tr>
</table>
indentation des structures de contrôle¶
print "bloc1"
if (condition1) :
print "bloc2"
if (condition2) :
print "bloc3"
print "bloc2 suite"
print "bloc1 suite"
tests imbriqués¶
si (condition1) alors
instruction1
sinon si (condition2) alors
instruction2
sinon
instruction3
fin si
si i= 15
i divisible par 3 mais pas par 2
erreur de syntaxe: attention à l’indentation et au symbol :¶
File "<ipython-input-9-5162c46baa06>", line 4
else
^
SyntaxError: invalid syntax
Problème: étant donné un nombre entier positif p, est-il pair ou impair ?
ALGORITHME Parite
Initialisez p
si (p modulo 2) == 0 alors
Affiche "p est pair"
sinon
Affiche "p est impair"
fin si
valeur p = 17
p est impair.
- nombre d’itérations n connues
- compteur de boucle i (variable)
- attention en algorithmique on compte en général à partir de 0
- premier élément d’une séquence i=0
Organigramme et algorithme¶
Out[11]:
| Algorithme | Diagramme |
|---|
pour i de 0 a n-1
execute intruction(s) 1
fin pour
execute instruction(s) 2
|
|
syntaxe Python¶
| Algorithmique | Python |
|---|
**boucle
par défaut** |
pour i de 0 a n-1
instructions 1
fin pour
instructions 2
|
for i in range(n):
instruction1
instruction2
| </tr>
**boucle
générale** |
pour i de p a n-1 pas q
instructions 1
fin pour
instruction2
|
for i in range(p, n, q):
instruction1
instruction2
| </tr>
</table>
0
1
2
3
range(0, 4)
1
3
range(1, 4, 2)
Itération: répétition d’instructions un nombre fini de fois
boucle itérative avec un compteur
Pour i=0,1,..,n-1
instruction
Fin Pour
exemple: calcul de la somme $S$ des $n$ premiers entiers $i$ positifs ou nul:
$$S=\sum_{i=0}^{n-1} i $$
Organigramme: tableau des variables¶
Out[13]:
| Algorithme | Tableau de variables |
|---|
1. S=0.
2. initialise n
3. pour i de 0 a n-1
4. S = S + i
5. fin i
6. affiche S
|
|
0 0
1 1
3 2
6 3
10 4
15 5
21 6
28 7
Somme (des 8 premiers entiers >= 0) S = 28
Algorithme itératif dont le nombre d’itérations n’est pas connu à l’avance.
| Algorithmique | Python |
|---|
Tantque (condition vrai)
instruction(s) 1
Fin Tantque
instructions 2
|
while condition:
instruction1
instruction2
|
Calcul de la somme de la série $\frac{x^i}{i!}$ avec une précision $\epsilon$ fixée
$$ S = \sum_i \frac{x^i}{i!} \mbox{ pour tout } i \mbox{ t.q.} \frac{x^i}{i!} > \epsilon $$
Algorithme¶
ALGORITHME somme
initialiser x,eps
S = 0.
i = 0
term = 1.
tant que (term > eps) repeter
S = S + term
i = i + 1
term = term * x / i
afficher "Somme = ",S
Somme S = 2.7182818284467594 avec 14 termes
questions¶
- l’algorithme fonctionne-t-il pour x<0 ?
la valeur de la condition ne devient jamais fausse => itération infinie
Erreur: la condition n’est pas modifiée¶exemple
condition=True
i=0
while condition :
i=i+1
print i
exemple
x = 0.0
while (x != 1.0) :
x = x + 0.1
print x
0.1
0.2
0.30000000000000004
0.4
0.5
0.6
0.7
0.7999999999999999
0.8999999999999999
0.9999999999999999
1.0999999999999999
x = 1.0999999999999999 11
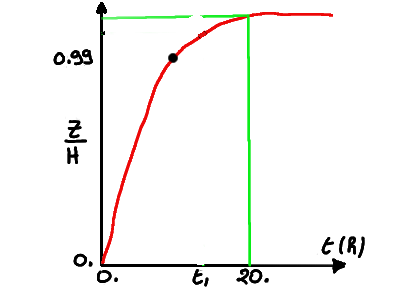
méthode de dichotomie¶On suppose que pendant son lancement, l’altitude $z(t)$ d’un satellite est donnée par:
$$z(t) = H * tanh(\frac{t}{T}) \mbox{ avec } T = 5 h $$
Au bout de $20 h$ le satellite atteint son orbite.
Au bout de quel temps $t_1$ le satellite atteint-il son orbite à $1\%$ près i.e calculer $t_1$ tel que:
$$ z(t_1)=0.99*z(20) $$
On déterminera la valeur de $t_1$ à 0.1h près en utilisant une méthode de dichotomie.
schéma
Solution algorithme de dichotomie¶
ALGORITHME Dichotomie
a = 0.
b = 20.
z0 = 0.99*tanh(b/5.)
tant ((b-a)>0.1) repeter
t = (a+b)/2.
si tanh(t/5.) > z0 alors
b = t
sinon
a = t
fin si
fin tant
Affiche "Temps t =", t
z0 = 0.899396369765
a= 0.0 b= 20.0 t= 10.0 z= 0.964027580076
a= 0.0 b= 10.0 t= 5.0 z= 0.761594155956
a= 5.0 b= 10.0 t= 7.5 z= 0.905148253645
a= 5.0 b= 7.5 t= 6.25 z= 0.848283639958
a= 6.25 b= 7.5 t= 6.875 z= 0.879826699652
a= 6.875 b= 7.5 t= 7.1875 z= 0.8931933404
a= 7.1875 b= 7.5 t= 7.34375 z= 0.899338734805
a= 7.34375 b= 7.5 t= 7.421875 z= 0.902284442756
Temps 7.421875
Méthode des trapèzes¶calcul de la valeur approchée de l’intégrale $\int_a^b{f(x)dx}$
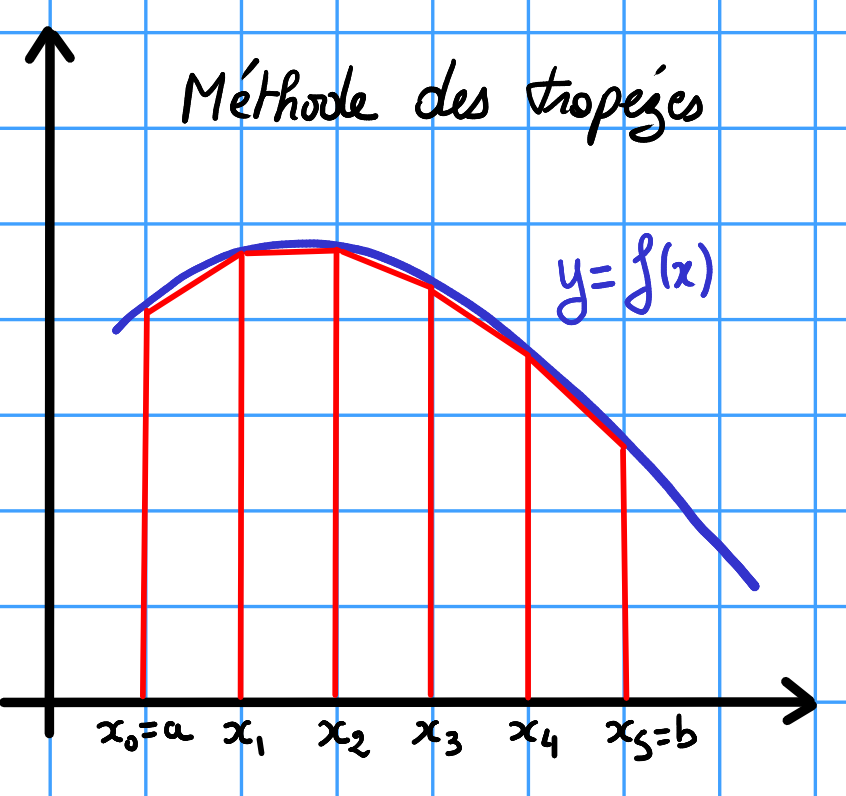
$$ \int_a^b{f(x)dx} \approx \sum_{i=1}^n{h \frac{f(x_i)+f(x_{i-1})}{2}} \mbox{ avec } x_i=a+ih \ ,\ h=\frac{b-a}{n}$$ Ecrire un programme Python qui calcule une estimation de
$$ I=\int_0^\pi{\frac{sin(x)}{x}dx} $$
validation¶$$ I=si(\pi)\approx 1.85193705198247$$
Calcul de la suite de Syracuse¶Écrire un programme qui calcule la suite d’entiers définie par
la règle suivante:
- on part d’un nombre entier n plus grand que zéro; s’il est pair, on le divise par 2 ; s’il est impair, on le multiplie par 3 et on ajoute 1
- on recommence et on s’arrête lorsque l’on arrive à 1
La conjecture de Collatz, énoncée en 1937, postule que cette suite de Syracuse s’arrête au bout d’un nombre fini d’itérations.
validation¶Pour n=3, on obtient la suite suivante: 3, 10, 5, 16, 8, 4, 2, 1
|
¶
