- ven. 15 janvier 2016
- INPROS
- #ipython jupyter
Ipython notebook : cours INPROS  ¶
¶
Auteur: Marc BUFFAT, Pr dpt de Mécanique, UCB Lyon 1
Contributeurs: Violaine Louvet, Michel Kern, Loic Gouarin, Laurence Viry </h5>

Mise à disposition selon les termes de la Licence Creative Commons
Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 2.0 France.
%matplotlib inline
%autosave 300
import numpy as np
from IPython.display import HTML,display
css_file = 'style.css'
try:
display(HTML(open(css_file, "r").read()))
print("using ",css_file)
except :
print("using default css")



Fonction en Python¶
implémentation d’une procédure = function (C, Python) , subroutine (Fortran)
# définition
def MaFonction(liste arguments):
instructions
....
return (liste de valeurs)
# utilisation
(val1, val2, ..) = MaFonction(arg1, arg2, ...)
Passage des arguments¶
on affecte aux arguments de la fonction la valeur des paramètres d’appel:
def MaFonction(a1, a2, a3):
....
return (v1, v2)
(V1, V2) = MaFonction(A1, A2, A3)
- lors de l’appel, on a a1=A1 a2=A2 a3=A3
valeur de retour = liste
- lors du retour, V1=v1, V2=v2
**Exemple Python**(visualisation avec [http://www.pythontutor.com])
HTML('<iframe width="800" height="400" frameborder="0" src="http://pythontutor.com/iframe-embed.html#code=def+MaFonc(a1,a2,a3)%3A%0A++++v1%3Da1%2Ba3%0A++++v2%3Da2%2Ba3%0A++++return+(v1,v2)%0A%09%0AA1%3D1.%0A(V1,V2)%3DMaFonc(A1,2.,4*A1)&cumulative=false&heapPrimitives=false&drawParentPointers=false&textReferences=false&showOnlyOutputs=false&py=2&curInstr=8&codeDivWidth=350&codeDivHeight=400"> </iframe>')
Passage des arguments¶
pour les variables scalaires: valeur = valeur de la variable
- la variable n’est donc pas modifiée
pour les listes et tableaux: valeur = adresse des données
- on peut donc modifier la valeur d’une liste ou tableau en argument
- mais à condition de ne pas faire de réaffectation **Exemple Initialisation de liste (tableau) : version 1**
HTML('<iframe width="800" height="400" frameborder="0" src="http://pythontutor.com/iframe-embed.html#code=def+InitTab(X)%3A%0A%09X%5B%3A%5D%3D%5B0,0,0%5D%0A%09n%3Dlen(X)%0A%09for+i+in+range(n)%3A%0A%09++++++++X%5Bi%5D%3Di*i%0A%09return%09%0AZ%3D%5B1,1,1%5D%0AInitTab(Z)&cumulative=false&heapPrimitives=false&drawParentPointers=false&textReferences=false&showOnlyOutputs=false&py=2&curInstr=15&codeDivWidth=350&codeDivHeight=400"> </iframe>')
HTML('<iframe width="800" height="400" frameborder="0" src="http://pythontutor.com/iframe-embed.html#code=def+InitTab(X)%3A%0A++++X%3D%5B0,0,0%5D%0A++++n%3Dlen(X)%0A++++for+i+in+range(n)%3A%0A++++++++X%5Bi%5D%3Di*i%0A++++return%09%0AZ%3D%5B1,1,1%5D%0AInitTab(Z)&cumulative=false&heapPrimitives=false&drawParentPointers=false&textReferences=false&showOnlyOutputs=false&py=2&curInstr=15&codeDivWidth=350&codeDivHeight=400"> </iframe>')
Algorithme d’Euclide: calcul du PGCD de 2 entiers¶
# Calcul du PGCD
# paramètres d'entrée: 2 entiers positifs a et b
# en sortie: PGCD de a et b
#
Algorithme PGCD(a,b)
tant que a # b
si a>b alors a = a-b
sinon b = b - a
retour a
#
Programme Python¶
def PGCD(a, b):
"""
Calcul du PGCD de a et b (entiers positifs)
"""
while a != b:
if a > b:
a = a - b
else:
b = b - a
return a
# utilisation
a0, b0 = 15623532, 252568
p = PGCD(a0, b0)
print("PGCD de ", a0, b0, "=", p)
Algorithme: calcul de la somme d’une série¶
$$ S_n = \sum_{i=1}^n \frac{1}{i^2} \mbox{ et } \lim_{n\rightarrow\infty} S_n = \frac{\pi^2}{6}$$# calcul de la somme Sn et de l'Écart par rapport à la limite
# entrée: n entier sortie: somme, écart par rapport à limite
Algorithme Somme(n)
S=0.
pour i de 1 a n
S = S + 1./i**2
err = S - (pi**2/6.)
retour S,err
Programme Python¶
# fonction Python
def Somme(n):
"""
Calcul de la somme de la série 1/i**2 pour i de 0 a n
en sortie: somme et écart par rapport à la limite
"""
S=0.
for i in range(1, n + 1):
S = S + 1. / (i*i)
ecart = S - (np.pi**2/6.)
return S, ecart
#
n = 100
S, err = Somme(n)
print(S, err)
print(Somme(1000))
print(Somme(10000))
Paramètres optionnels d’une fonction¶
- En Python possibilité de définir des paramètres optionnels avec une valeur par défaut
- Nommage des paramètres (ordre indifférent)
- Très utilisés dans les fonctions des bibliothèques
# Déclaration
def MaFonction(par, par1=valdef1, par2=valdef2)
# Appel
MaFonction(val)
MaFonction(val, par1=val1)
MaFonction(val, par2=val2, par1=val1)
Exemple: algorithme de Héron pour calculer une racine carrée¶
Pour calculer une approximation $u$ de $\sqrt{a}$, on note que si $u\approx\sqrt(a)$ alors $a/u\approx\sqrt(a)$ et donc $\frac{u + a/u}{2}$ est sans doute une meilleur approximation de $\sqrt{a}$.
On peut vérifier que cette méthode babylonienne est en fait un cas particulier de la méthode de Newton pour calculer la racine de $f(x)=u^2-a$
Algorithme¶
Algorithme Heron(a)
u = a/2
eps = 1.e-6
tant que |u**2 - a| > eps
u = (u + a/u)/2
fin tantque
retour u
Programme Python¶
import numpy as np
def Heron(a, eps=1e-03, itmax=100):
"""
calcul une approximation de sqrt(a) avec une precision eps
et une nombre maxi d'iterations itmax """
u = a/2.
it = 0
while abs(u**2 - a) > eps:
u = (u + a/u) / 2.
it = it + 1
if it > itmax:
print("Attention nbre maxi d'iterations atteint", it)
break
return u, it
# utilisation
b = 200.
print("sqrt(200) ~",Heron(b))
print("a 10^-8 pres sqrt(200) ~",Heron(b, 1.e-08))
print("a 10^-13 pres sqrt(200) ~",Heron(b, eps=1.e-13))
print("a 10^-14 pres sqrt(200) ~",Heron(b, eps=1.e-14))
print("a 10^-14 pres sqrt(200) ~",Heron(b, itmax=200, eps=1.e-14))
print("valeur avec numpy ",np.sqrt(b),repr(np.sqrt(b)))
Fonction Lambda¶
- permet de définir des mini-fonctions (à la Lisp)
- utile pour des fonctions simples (mais pas obligatoire!!)
F = lambda args : expression(args)import numpy as np
F = lambda x: np.cos(x**2)
print(F(1))
G = lambda x, y: F(x) + y**2
print(G(1, 1))
Méthodes, classes et fonctions de bibliothéque¶
Définition¶
classe = type de structure de données définissant des données + fonctions pour manipuler ces données
méthode = fonction associée à une classe pour manipuler les données de la classe
objet = instance de classe = variable [données + méthodes]
sous Python toute variable (list, string, real, int) est un objet et possède des méthodes (p.e pour l’afficher)
Syntaxe d’utilisation d’une méthode sous Python¶
pour un objet A avec un methode func1
A.func1(arg1,arg2,...)
équivalent à
func1(A,arg1,arg2,..)
Exemple en Python¶
S="mon nom"
print(S.upper())
L=[1,2,3]
L.reverse()
print(L)
X=3.14157
print(X.as_integer_ratio())
Aide sous Ipython¶
Sous Ipython, pour avoir la liste des méthodes associées à un objet A
A. <tab> # liste des methodes
A.meth? # aide sur la methode methL
Fonctions d’une bibliothéque¶
espace de nom = nom de la bibliothéque bibli
import bibli
nom de la fonction func dans la bibliothéque
bibli.func
bibli.sous_bibli.func
simplification du nommage
import bibli as bib
import bibli.sous_bibli as sbib
importation d’une fonction
from bibli import funcimport numpy as np
print(np.sqrt(3))
from numpy import tanh
print(tanh(1))
Programmation structurée¶
principe: “Divide and Conquer”
découpage du problème en une suite de problèmes plus simples
Analyse algorithmique “Top-Down design”¶
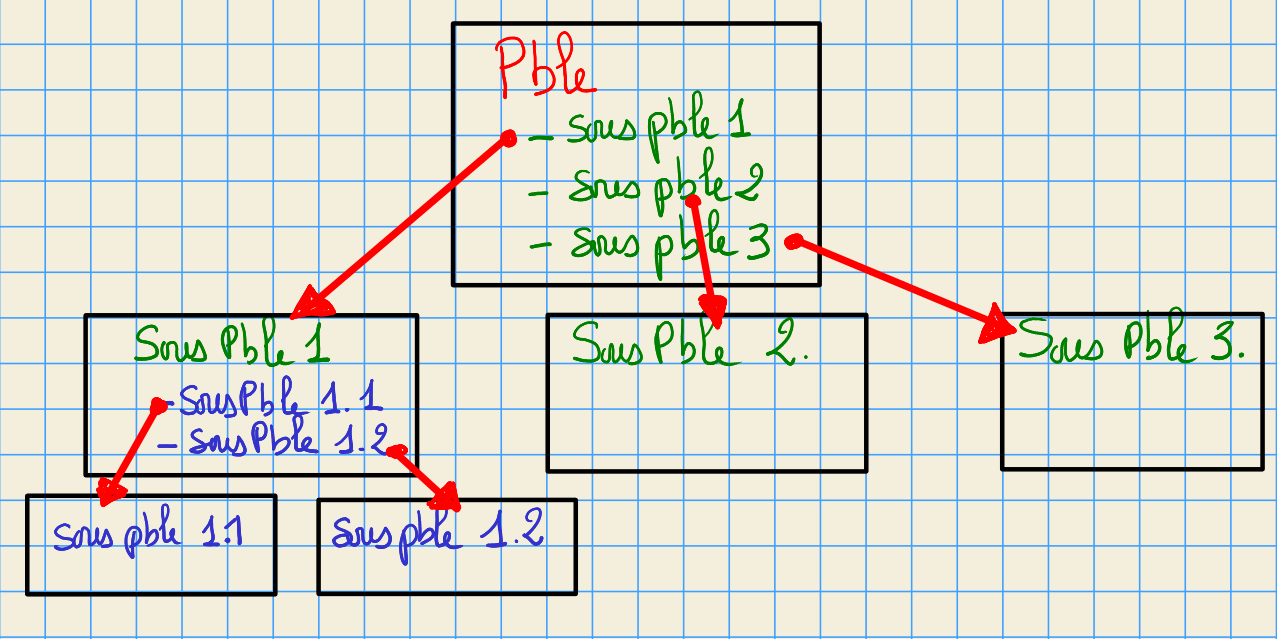
Principes de l’analyse top down¶
- on découpe le problème en une série de sous-problèmes plus simples (si possible indépendant)
- on spécifie ce qui doit résolu dans chacun des sous-problèmes sans forcément dire comment
- puis on itère au niveau des sous problèmes.
Programmation “Botton-up programming”¶
- on part des sous-problèmes élémentaires que l’on programme sous forme de fonctions (ou procédures)
- on valide les fonctions
- puis on réitère en remontant dans l’arbre jusqu’au programme principal
règles réutiliser les fonctions déjà écrites et validées (bibliothèques): principe du moindre effort !
Exemple: simuler l’alunissage de Neil Amstrong (Apollo 11)¶
- basé sur une simulation d’alunissage du module lunaire écrit en basic en 1969, puis popularisé en 1979 sur ATARI (Lunar Lander).
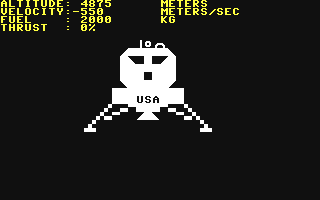
jeu “Lunar Lander”:¶
Poser le module lunaire (LEM) sur la lune en arrivant avec une vitesse quasiment nulle. Pour cela on dispose de rétro-fusées permettant de ralentir la chute du LEM.
- On contrôle manuellement ces rétro-fusées en sélectionnant une poussée (de 0 à 9), correspondant à l’éjection de carburant avec un débit $Qe$ variable et une vitesse $Ue$ fixe.
- Mais on dispose d’une quantité limitée de carburant que l’on doit utiliser avec modération pour pouvoir atterrir en douceur.
modèle physique:¶
Le LEM, de masse initiale $M0$, est soumis à la gravité $g$ de la lune et à la poussée des rétro-fusées, correspondant à l’éjection d’un débit de fuel $Qe$ à un vitesse $Ve$ .
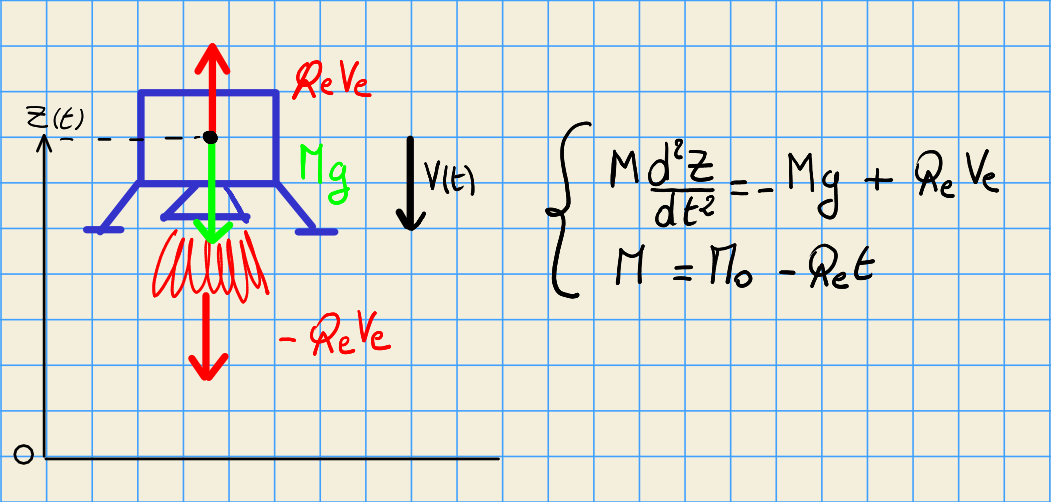
modèle mathématique:¶
Equation du mouvement: $$ \frac{d^2 Z}{dt^2} = -g + \frac{Qe*Ue}{M0-Qe*t}$$
en intégrant sur la durée d’une commande $T$ $\rightarrow$ vitesse $V$ $$ V = V0 + g*T + Ue * \ln{(1 - \frac{Qe*T}{M0})} $$ La masse du LEM $M$ diminue $$M = M0 -Qe*T$$ Approximation par DL car $X=\frac{Qe*T}{M0} \ll 1$ $$ V = V0 + g*T - Ue*(X + \frac{X^2}{2} + \frac{X^3}{3} + \frac{X^4}{4} + \frac{X^5}{5})$$ d’où l’altitude $Z$ $$ Z = Z0 - V0*T - g \frac{T^2}{2} + Ue*T*(\frac{X}{2} + \frac{X^2}{6} + \frac{X^3}{12} + \frac{X^4}{20} + \frac{X^5}{30})$$ expression utilisée dans les premiers programmes en BASIC.
cas particuliers¶
Si le fuel est épuisé ($Qe=0$), le LEM atteins la surface lunaire au bout d’un temps $T$ solution de l’équation du 2nd degré: $$ 0 = Z0 - V0*T -g \frac{T^2}{2}$$ soit $T = (-V0 + \sqrt{V0^2 + 2 g Z0})/g$
Près de la surface, $T$ trop grand $\rightarrow$ prédiction $Z0 < 0$
- calcul $T$ donnant l’altitude $Z=0$, solution d’une équation du 6ième degré.
- calcul par approximations successives en utilisant un DL de $Z(t)$
- estimation $T0$ de $T$ $$ T0 = \frac{-V0 + \sqrt{V0^2 + 2 (g-\frac{Ue*Qe}{M0}) Z0}}{g-\frac{Ue*Qe}{M0}} $$
- recalcule $V0$ et $Z0$, puis recommence.
Algorithme: analyse top-down¶
problème global¶

sous-probleme Lecture_cde¶

sous-problème VitesseAltitude¶
applications des formules mathématiques de l’analyse précédente
$$ V = V0 + g*T - Ue*(X + \frac{X^2}{2} + \frac{X^3}{3} + \frac{X^4}{4} + \frac{X^5}{5})$$$$ Z = Z0 - V0*T - g \frac{T^2}{2} + Ue*T*(\frac{X}{2} + \frac{X^2}{6} + \frac{X^3}{12} + \frac{X^4}{20} + \frac{X^5}{30})$$sous-probleme Alunissage¶
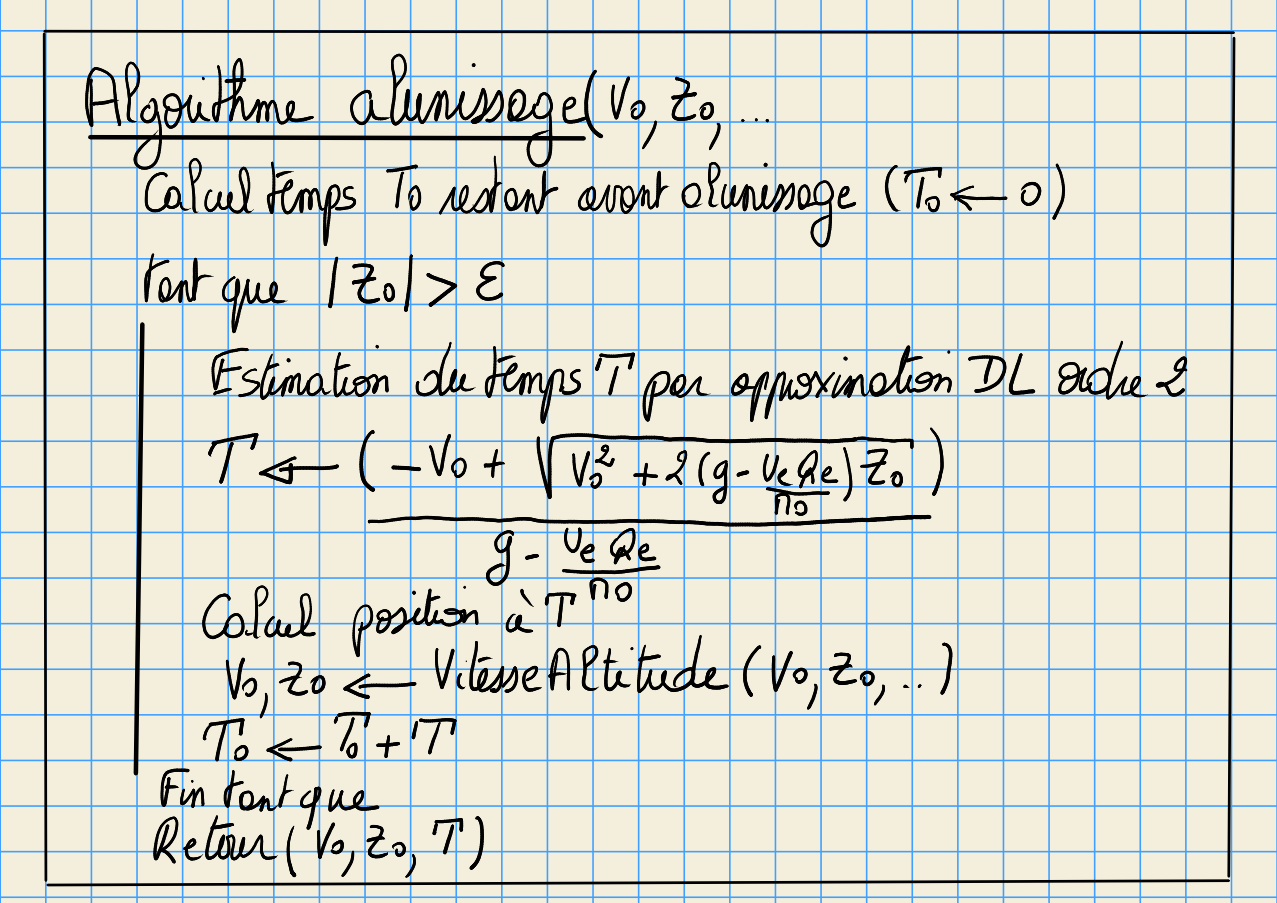
import numpy as np
import sys
# constantes en unité SI (kg/m/s)
g = 1.6 # gravité
Ue = 2900. # vitesse d'ejection
#
def Lecture_Cde(Me,dt):
""" lecture de la commande (poussée) avec test carburant """
T=dt
if Me>0 :
# lecture poussee
while True:
ch = input("Entrez la valeur de la poussée (0-9) (en 10eme kg/s) = ")[0]
if (ch>='0') and (ch<='9') :
Qe = int(ch)*10 # pousse en kg/s
break;
if (ch=='Q') : sys.exit(1)
print("Erreur: entrer un chiffre entre 0 et 9 ")
# test si reserve de fuel suffisante
if (Me-Qe*T)<0 :
# temps restant d'utilisation du fuel
T = Me/Qe
else:
print("Plus de fuel ")
Qe = 0
# calcul du temps T pour parcourir Z0 (alunissage)
T = (-V0 + np.sqrt(V0*V0 + 2*g*Z0)) / g
return Qe,T
def VitesseAltitude(v0,Z0,X,T):
""" calcul de la nvlle vitesse en fonction de la vitesse init V0
un débit sans dimension X=Qe*T/M0 de fuel, pendant un temps T
ainsi que de la nouvelle altitude du LEM
"""
global g,Ue
V = V0 + g*T - Ue*(X + X*X/2. + X**3/3. + X**4/4. + X**5/5.)
Z = Z0 - V0*T - g*T*T/2. + Ue*T*(X/2. + X*X/6. + X**3/12. + X**4/20. + X**5/30.)
return V,Z
def Alunissage(V0,Z0,M0,Qe):
""" calcul etat a Z=0 a partir d'une CI V0,Z0,M0 et une poussée Qe """
global g,Ue
# calcul du temps T pour alunissage par approximation successive
T0 = 0
while np.abs(Z0) > 1.e-2:
T= (-V0 + np.sqrt(V0*V0 + 2*(g-Ue*Qe/M0)*Z0)) / (g-Ue*Qe/M0)
V0,Z0 = VitesseAltitude(V0,Z0,Qe*T/M0,T)
T0 = T0+ T
return V0,Z0,T0
# conditions initiales
Z0 = 190000. # position
V0 = 1580. # et vitesse
M0 = 15000. # masse initiale du LEM
Me = 8000. # dont une masse de fuel
t = 0. # temps simulation
dt = 10. # pas en temps entre chaque commande
#
print("Simulation alunissage")
while np.abs(Z0)>1.e-2 :
Qe,T = Lecture_Cde(Me,dt)
# calcul de la nouvelle position du LEM
V1,Z1 = VitesseAltitude(V0,Z0,Qe*T/M0,T)
# test si alunnissage
if Z1 < 1.e-2 :
V1,Z1,T = Alunissage(V0,Z0,M0,Qe)
# mise a jour de la position du LEM
Z0 = Z1; V0 = V1
Me = Me-Qe*T; M0 = M0-Qe*T
t = t + T
print("t=",int(t),"s Z=",int(Z0),"m V=",int(V0),"m/s fuel=",int(Me),"kg")
# fin simulation
print("Alunissage avec une vitesse ",int(V0)," m/s")
if V0<=0.5 :
print("Alunissage parfait")
elif V0<=5. :
print("Bon alunissage, mais perfectible")
elif V0<=27.:
print("Accident à l'alunissage. Attendez les secours en esperant que vous avez assez d'oxygene !!!")
else :
print("Crash fatal: aucun survivant")
Exercice: simulation d’un lancer de balle¶

Modèle physique:¶
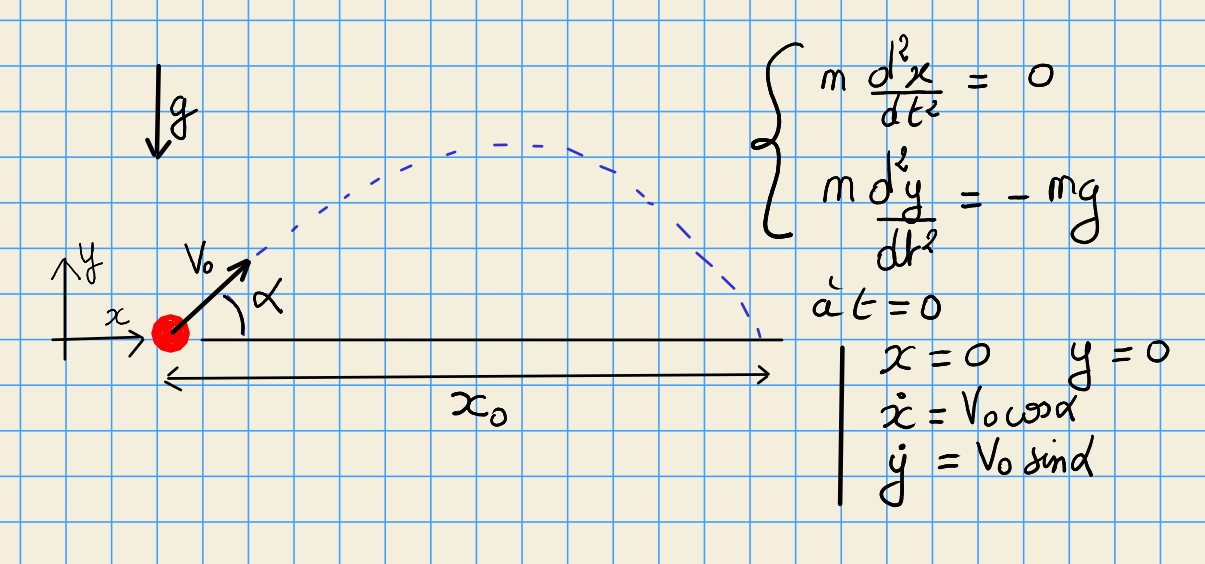
Modèle mathématique:¶
Ce modèle admet une solution analytique simple pour la position $x_0$
$$ x_0 = \frac{ 2 V_0^2 \sin{\alpha} \cos{\alpha}}{g} $$Objectif du programme¶
Écrire un programme Python qui simule le jeux angry birds en mode texte. On pose un bloc à une distance $L$ du joueur, qui doit envoyer une balle pour le démolir (i.e. atteindre $L$ avec une précision donnée).
Le joueur choisit 2 paramètres à valeurs discrètes:
- l’angle $\alpha$ (de 1 à 8 pour un angle de 10 à 45 degré par pas de 5)
- la vitesse initiale $V_0$ (de 1 à 5 par pas 1).
Le joueur a 3 essais, et pour chaque essai, le programme indique la distance atteinte par la balle par rapport au bloc visé.
Bibliographie¶
Programme originel “Lunar Lander” en Basic sur ATARI:
“Lunar Lander basic programme”Les classes sous Python
“Classes sous Python”,
chapitre du livre “Apprendre à programmer avec Python”Livre sur Python
(en téléchargement gratuit) “Apprendre à programmer avec Python” de Gérard Swinnen


