Structures de contrôle

Contenu

5. Structures de contrôle#

%matplotlib inline
import numpy as np
from IPython.display import HTML,display,IFrame,Video
from IPython.display import YouTubeVideo,Markdown

display(Markdown("**Video du cours: Introduction**"))
YouTubeVideo('iKoa5WBKOVA')

Video du cours: Introduction

Astuce

pour tester les programmes Python, vous pouvez vous connectez sur un serveur Jupyter, par exemple, pour les étudiants Lyon1 https://jupyter.mecanique.univ-lyon1.fr

5.1. Expression logique#

expression	notation algorithmique	syntaxe Python
valeur logique	Vrai , Faux	True (\(\neq 0\)) , False(\(= 0\))

opérateurs logiques	et , ou , non	and , or , not

comparaisons	supérieur, supérieur ou égale	> , >=
« «	inférieur, inférieur ou égale	< , <=
« «	égalité	==
« «	différence	!=

display(Markdown("**Video du cours: expression logique et test**"))
YouTubeVideo('5oCl0q6lQRw')

Video du cours: expression logique et test

Attention

Les vidéos utilisent un ancien interpréteur python 2.7, pour lequel print est un mot clé, soit print 'bonjour'. Avec Python 3, print est une fonction et il faut donc utiliser des parenthèses, soit print('bonjour')

5.1.1. Exemple en Python#

print(type(True))
print(True and False)
print(False or True)
a = 4
print(a < 4, a <= 4, a >= 4, a > 4, a == 5, a != 5 , not (a == 5))
print(True + False)

<class 'bool'>
False
True
False True True False False True True
1

5.2. Test conditionnel (branchement)#

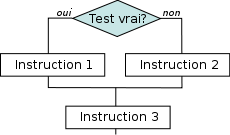
5.2.1. Organigramme: représentation graphique d’un algorithme#

Algorithme

    si (test vrai) alors
       intruction(s) 1
    sinon
       intruction(s) 2
    fin si
    instruction(s) 3

from diagramme1 import trace_diagramme1
HTML(trace_diagramme1())

5.2.2. syntaxe Python#

notation algorithmique

si (expression vrai) alors   
     execute intruction(s) 1  
sinon
     execute intruction(s) 2
fin si
execute instruction(s) 3

syntaxe Python (noter les :)

if expression :
    intruction1
else :
    intruction2
    
instruction3

5.2.3. indentation des structures de contrôle#

print "bloc1"
if (condition1) :
   print "bloc2"
   if (condition2) :
       print "bloc3"
   print "bloc2 suite"
print "bloc1 suite"

5.2.4. tests imbriqués#

si (condition1) alors
    instruction1
sinon si (condition2) alors
    instruction2
sinon
    instruction3
fin si

i=15
print("si i=",i)
if i%2 == 0 :
    print("i divisible par 2")
elif i%3 == 0 :
    print("i divisible par 3 mais pas par 2")
elif i%5 == 0 :
    print("i divisible par 5 mais pas par 2 ni 3")
else :
    print("i non divisible par 2,3 et 5")

si i= 15
i divisible par 3 mais pas par 2

5.2.5. erreur de syntaxe: attention à l’indentation et au symbol :#

a = 4
if a > 5:
    print("a est plus grand que 5")
else
    print("a est plus petit ou egal a 5")

File "<ipython-input-7-5162c46baa06>", line 4
else
    ^
SyntaxError: invalid syntax

5.2.6. Exemple d’application#

Problème: étant donné un nombre entier positif p, est-il pair ou impair ?

ALGORITHME Parite
  Initialisez p
  si (p modulo 2) == 0 alors
     Affiche "p est pair"
  sinon
     Affiche "p est impair"
  fin si

5.2.7. Programme Python#

# programme parite
p = 17
print("valeur p =", p)
if p%2 == 0:
    print("p est pair.")
else:
    print("p est impair.")

valeur p = 17
p est impair.

5.3. Boucle itérative#

nombre d’itérations n connues
compteur de boucle i (variable)
attention en algorithmique on compte en général à partir de 0
premier élément d’une séquence i=0

display(Markdown("**Video du cours: boucle itérative pour**"))
YouTubeVideo('2fv2KdqMr2o')

Video du cours: boucle itérative pour

Attention

Les vidéos utilisent un ancien interpréteur python 2.7, pour lequel print est un mot clé, soit print 'bonjour'. Avec Python 3, print est une fonction et il faut donc utiliser des parenthèses, soit print('bonjour')

5.3.1. Organigramme et algorithme#

Algorithme

pour i de 0 a n-1
   execute intruction(s) 1
fin pour
execute instruction(s) 2

from diagramme2 import trace_diagramme2
HTML(trace_diagramme2())

5.3.2. syntaxe Python#

Algorithmique

boucle par défaut (n itérations qui débute à 0 avec un incrément de 1)
```
  pour i de 0 a n-1
     instructions 1
  fin pour
  instructions 2
```

boucle générale (n-p)/q itérations qui débute à p avec un incrément q)

  pour i de p a n-1 pas q 
     instructions 1
  fin pour
  instruction2

Syntaxe Python

boucle par défaut noté l’utilisation de n (nbre d’itérations) et non n-1 (valeur max de i)
```
  for i in range(n):
         instruction1
  instruction2
```
boucle générale noté que la dernière valeur n est exclue pour que le nbre d’itérations soit égale à (n-p)/q
```
  for i in range(p, n, q):
     instruction1
  instruction2
```

5.3.3. Exemples en Python#

for i in range(4):
    print(i)
print(range(4))
for j in range(1, 4, 2):
    print(j)
print(range(1, 4, 2))

0
1
2
3
range(0, 4)
1
3
range(1, 4, 2)

5.4. Algorithme itératif#

Itération: répétition d’instructions un nombre fini de fois

boucle itérative avec un compteur

  Pour i=0,1,..,n-1
      instruction
  Fin Pour

exemple: calcul de la somme \(S\) des \(n\) premiers entiers \(i\) positifs ou nul:

\[S=\sum_{i=0}^{n-1} i \]

5.4.1. Organigramme: tableau des variables#

Algorithme

S=0.
initialise n
pour i de 0 a n-1
  S = S + i
fin i
affiche S

from boucle1 import trace_boucle1
HTML(trace_boucle1())

5.4.2. Programme en Python#

# programme de calcul de la somme de n entiers
S = 0
n = 8
for i in range(n):
    S = S + i
    print(S, i)
print("Somme (des ", n, " premiers entiers >= 0)  S =", S)

0
1
2
3
4
5
6
7
Somme (des  8  premiers entiers >= 0)  S = 28

5.4.3. Visualisation de l’exécution du code Python#

utilisation du site : http://pythontutor.com

vous pouvez copier l’exemple de code python sur le site pour l’exécuter

display(Markdown("**Visualisation de l'execution sur le site pythontutor**"))
Video("VIDEO_COURS/pythonlive_loop.mp4", embed=True,width=700, height=300)

Visualisation de l’execution sur le site pythontutor

5.5. Boucle tant que#

Algorithme itératif dont le nombre d’itérations n’est pas connu à l’avance.

notation algorithmique

Tantque (condition vrai)
    instruction(s) 1
Fin Tantque
instructions 2

Syntaxe python

while condition :
    instruction1
instruction2

display(Markdown("**Video du cours: boucle itérative tantque**"))
YouTubeVideo('i2qCuRP3uUk')

Video du cours: boucle itérative tantque

Attention

Les vidéos utilisent un ancien interpréteur python 2.7, pour lequel print est un mot clé, soit print 'bonjour'. Avec Python 3, print est une fonction et il faut donc utiliser des parenthèses, soit print('bonjour')

5.5.1. Exemple de boucle tant que#

Calcul de la somme de la série \(\frac{x^i}{i!}\) avec une précision \(\epsilon\) fixée

\[ S = \sum_i \frac{x^i}{i!} \mbox{ pour tout } i \mbox{ t.q.} \frac{x^i}{i!} > \epsilon \]

5.5.2. Algorithme#

ALGORITHME somme
initialiser x,eps
S = 0.
i = 0
term = 1.
tant que (term > eps) repeter
    S = S + term
    i = i + 1
    term = term * x / i
afficher "Somme = ",S

5.5.3. Programme Python#

# programme somme
x = 1.
eps = 1.0e-10
S = 0.
i = 0
term = 1.
while term > eps:
    S = S + term
    i = i + 1
    term = term * x / i
print("Somme S =", S, " avec ", i, " termes")

Somme S = 2.7182818284467594  avec  14  termes

# verification
print(np.exp(x))

2.718281828459045

5.5.4. questions#

l’algorithme fonctionne-t-il pour x<0 ?

5.5.5. Visualisation de l’execution du code Python#

utilisation du site : http://pythontutor.com

vous pouvez copier l’exemple de code python sur le site pour l’exécuter

display(Markdown("**Visualisation de l'execution sur le site pythontutor**"))
Video("VIDEO_COURS/pythonlive_pge.mp4", embed=True,width=700, height=300)

Visualisation de l’execution sur le site pythontutor

5.6. Erreurs courantes#

la valeur de la condition ne devient jamais fausse => itération infinie

5.6.1. Erreur: la condition n’est pas modifiée#

exemple

condition=True
i=0
while condition :   
   i=i+1
print i

# tester le code

code Python corrigé

condition = True
i = 0
while condition:
    i = i + 1
    condition = i < 10
print(i)

5.6.2. Erreur: la condition est trop contraignante (précision)#

exemple

x = 0.0
while (x != 1.0) :
   x = x + 0.1
print x

## test du code

solution introduire un compteur \(i\) et un test \(i>it_{max}\) avec un break

code python corrigé

x = 0.0
i = 0
while x != 1.0:
    x = x + 0.1
    print(repr(x))
    i = i + 1
    if i > 10: break
print("x =", x, i)

1
2
30000000000000004
4
5
6
7
7999999999999999
8999999999999999
9999999999999999
0999999999999999
x = 1.0999999999999999 11

5.7. Exemples#

display(Markdown("**Video du cours: exemples et exercices d'application**"))
YouTubeVideo('uk4AwYc7NhY')

Video du cours: exemples et exercices d’application

Attention

Les vidéos utilisent un ancien interpréteur python 2.7, pour lequel print est un mot clé, soit print 'bonjour'. Avec Python 3, print est une fonction et il faut donc utiliser des parenthèses, soit print('bonjour')

5.7.1. méthode de dichotomie#

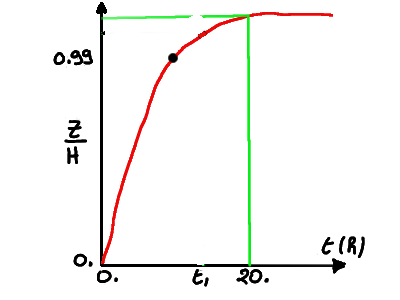
On suppose que pendant son lancement, l’altitude \(z(t)\) d’un satellite est donnée par:

\[z(t) = H * tanh(\frac{t}{T}) \mbox{ avec } T = 5 h \]

Au bout de \(20 h\) le satellite atteint son orbite.

Au bout de quel temps \(t_1\) le satellite atteint-il son orbite à \(1\%\) près i.e calculer \(t_1\) tel que:

\[ z(t_1)=0.99*z(20) \]

On déterminera la valeur de \(t_1\) à 0.1h près en utilisant une méthode de dichotomie.

schéma

5.7.2. Solution algorithme de dichotomie#

ALGORITHME Dichotomie
a = 0.
b = 20.
z0 = 0.99*tanh(b/5.)
tant ((b-a)>0.1) repeter
    t = (a+b)/2.
    si tanh(t/5.) > z0 alors
        b = t
    sinon
        a = t
    fin si
 fin tant
 Affiche "Temps t =", t

5.7.3. programme Python#

# programme dichotomie
import numpy as np
a = 0.
b = 20.
z0 = 0.9*np.tanh(b/5.)
print("z0 = ", z0)
while b - a > 0.1:
    t = (a+b) / 2.
    z = np.tanh(t/5.)
    print("a=", a, "b=", b, "t=", t, "z=", z)
    if z > z0:
        b = t
    else:
        a = t
print("Temps ", t)

z0 =  0.8993963697651604
a= 0.0 b= 20.0 t= 10.0 z= 0.9640275800758169
a= 0.0 b= 10.0 t= 5.0 z= 0.7615941559557649
a= 5.0 b= 10.0 t= 7.5 z= 0.9051482536448665
a= 5.0 b= 7.5 t= 6.25 z= 0.8482836399575129
a= 6.25 b= 7.5 t= 6.875 z= 0.8798266996519848
a= 6.875 b= 7.5 t= 7.1875 z= 0.8931933404003515
a= 7.1875 b= 7.5 t= 7.34375 z= 0.8993387348050462
a= 7.34375 b= 7.5 t= 7.421875 z= 0.9022844427556502
Temps  7.421875

5.8. Devoirs d’application#

5.8.1. Méthode des trapèzes#

calcul de la valeur approchée de l’intégrale \(\int_a^b{f(x)dx}\)

\[ \int_a^b{f(x)dx} \approx \sum_{i=1}^n{h \frac{f(x_i)+f(x_{i-1})}{2}} \mbox{ avec } x_i=a+ih \ ,\ h=\frac{b-a}{n}\]

Ecrire un programme Python qui calcule une estimation de

\[ I=\int_0^\pi{\frac{sin(x)}{x}dx} \]

5.8.1.1. validation#

\[ I=si(\pi)\approx 1.85193705198247\]

5.8.2. Calcul de la suite de Syracuse#

Écrire un programme qui calcule la suite d’entiers définie par la règle suivante:

on part d’un nombre entier n plus grand que zéro; s’il est pair, on le divise par 2 ; s’il est impair, on le multiplie par 3 et on ajoute 1

on recommence et on s’arrête lorsque l’on arrive à 1

La conjecture de Collatz, énoncée en 1937, postule que cette suite de Syracuse s’arrête au bout d’un nombre fini d’itérations.

5.8.2.1. validation#

Pour n=3, on obtient la suite suivante: 3, 10, 5, 16, 8, 4, 2, 1

5.9. Fin de la leçon#