

12. Algorithmes numériques#

%matplotlib inline
from IPython.display import HTML
import numpy as np
import matplotlib.pyplot as plt
plt.rc('font', family='serif', size='16')
12.1. Bibliothèques scientifiques sous Python#
documentation
Numercal Python numpy http://www.numpy.org/
Scientific Python scipy http://docs.scipy.org/doc/scipy/reference
12.2. Algorithme récursif#
récursion méthode algorithmique où la solution du problème s’exprime en fonction de solutions du même problème, mais sur des données plus petites.
Très utilisé en informatique, car fournit des solutions élégantes.
Attention, peut être inefficace (comparé à l’itération)
12.2.1. Exemple 1: calcul du PGCD de 2 entiers#
- PGCD(a,b)=PGCD(a-b,b) si a>b
- PGCD(a,b)=PGCD(b-a,a) si a<b
- PGCD(a,a)=a
12.2.1.1. Algorithme PGCD recursif#
Algorithme PGCD(a,b)
si a == b
retour a
sinon si a > b
retour PGCD(a-b,b)
sinon
retour PGCD(b-a,a)
12.2.1.2. Programme Python#
def PGCD(a,b):
print("appel PGCD(",a,",",b,")")
if a==b:
return a
elif a>b:
return PGCD(a-b,b)
else:
return PGCD(b-a,a)
#
print(PGCD(9,21))
appel PGCD( 9 , 21 )
appel PGCD( 12 , 9 )
appel PGCD( 3 , 9 )
appel PGCD( 6 , 3 )
appel PGCD( 3 , 3 )
3
12.2.2. Exemple 2: calcul du déterminant d’une matrice#
soit \(A\) une matrice d’ordre \(n\), la méthode de Cramer permet le calcul récursif du déterminant par développement par rapport à la 1ere colonne
où \(A^k\) est la sous-matrice obtenu par élimination de la colonne 1 et de la ligne \(k\) de \(A\)
Pour une matrice de dimension 1
12.2.2.1. Algorithme déterminant#
Algorithme determinant(A)
n = dim(A)
si n==1 alors
retour A[0,0]
fin si
# A1 sous matrice d'ordre n-1
A1 = tableau(n-1,n-1)
det = 0
signe = 1
# développement par rapport a la 1ere colonne
pour k de 0 a n-1
# sous matrice Ak
A1[0:k,:] = A[0:k ,1:n]
A1[k:,:] = A[k+1:,1:n]
det = det + signe*A[k,0]*determinant(A1)
signe = -signe
fin pour
retour det
12.2.2.2. Programme Python#
def determinant(A):
""" calcul du déterminant d'une matrice A """
n=A.shape[0]
print("determinant ",n)
if n==1 :
return A[0,0]
A1 = np.zeros((n-1,n-1))
det = 0.
signe = 1
for k in range(n):
if k>0:
A1[0:k,:] = A[0:k,1:n]
if k<n-1:
A1[k:,:] = A[k+1:n,1:n]
print("dvt ligne ",k,n)
det = det + signe*A[k,0]*determinant(A1)
signe = -signe
return det
#
M = np.array([[2.,0.,0],[0.,3.,0],[0,0,4.]])
delta = determinant(M)
determinant 3
dvt ligne 0 3
determinant 2
dvt ligne 0 2
determinant 1
dvt ligne 1 2
determinant 1
dvt ligne 1 3
determinant 2
dvt ligne 0 2
determinant 1
dvt ligne 1 2
determinant 1
dvt ligne 2 3
determinant 2
dvt ligne 0 2
determinant 1
dvt ligne 1 2
determinant 1
12.2.3. Exercise: tour de Hanoi#
Ecrire un algorithme récursif pour résoudre le problème des tours de Hanoi
12.3. Tri d’un tableau#
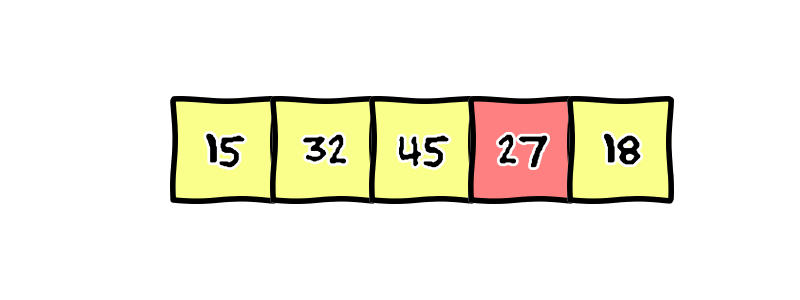
12.3.1. tri par insertion#
algorithme de tri classique: on compare successivement chaque élément du tableau en l’insérant au non endroit dans le tableau (méthode classique de tri d’un jeu de carte)
12.3.1.1. principe#
12.3.1.2. algorithme#
# Tri d'un tableau X de n éléments
Algorithme Tri_insertion(X)
n=dimension de X
pour i de 1 a n-1 faire # trie des élts
x = T[i] # élément a trier
j = i # position
tant que (j>0) et (T[j-1]>x) faire
T[j] = T[j-1] # permute j et j-1
j = j -1 # nouvelle position de x
fin tant que
T[j] = x # position de l’élément
fin i
retour # le tableau X est trie
Visualisation de l’algorithme en Python
#HTML('<iframe width="800" height="450" frameborder="0" src="http://pythontutor.com/iframe-embed.html#code=def+tri_insertion(X)%3A%0A++++n%3Dlen(X)%0A++++for+i+in+range(1,n)%3A%0A++++++++x%3DX%5Bi%5D%0A++++++++j%3Di%0A++++++++while+(j%3E0)+and+(X%5Bj-1%5D%3Ex)%3A%0A++++++++++++X%5Bj%5D+++%3D+X%5Bj-1%5D%0A++++++++++++j+%3D+j+-+1%0A++++++++X%5Bj%5D+%3D+x%0A++++return%0AX%3D%5B5,3,4,1%5D%0Atri_insertion(X)&cumulative=false&heapPrimitives=false&drawParentPointers=false&textReferences=false&showOnlyOutputs=false&py=2&curInstr=38&codeDivWidth=350&codeDivHeight=400"> </iframe>')
Efficacité \(O(n^2)\)
algorithme assez efficace pour \(n\) petit ou des tableaux presque triés
tri sur place
il existe des méthodes de tri plus efficaces (tri bulle, …)
12.3.2. Algorithme de tri de la bibliothéque numpy#
sort: méthode de trie plus efficace (tri rapide ou quicksort), renvoi le tableau trié
from numpy import *
X=array([5,3,4,1])
sort(X)
array([1, 3, 4, 5])
12.4. Recherche de la racine \(F(x)=0\)#
méthode itérative à partir d’une estimation \(x_0\)
methode de Newton: \(x_{n+1}= x_n - \frac{F(x_n)}{F'(x_n)}\)
méthode de la sécante: Newton avec \(F'(x_n) \approx \frac{F(x_n)-F(x_{n-1})}{x_n - x_{n-1}}\)
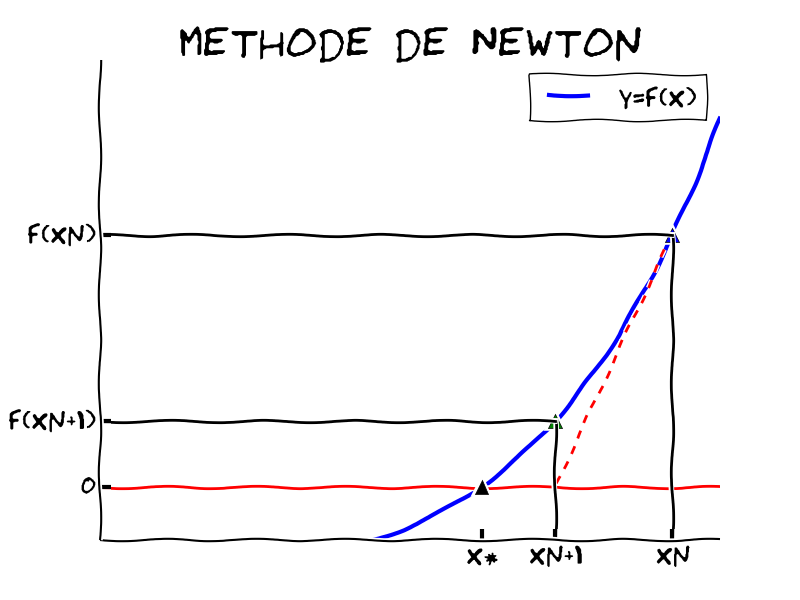
fonction fsolve dans scipy.optimize
généralisation dans \(\mathbf{R}^p\), on remplace \(F'(x_n)\) par la matrice Jacobienne \(J = \{\frac{\partial F_i}{\partial x_j}\} \)
from numpy import *
import matplotlib.pyplot as plt
from scipy.optimize import fsolve
# fonction et sa dérivée
def F(x):
return x+2*cos(x)
def dF(x):
return 1-2*sin(x)
# analyse
x0=0.
xe=fsolve(F,x0,fprime=dF)
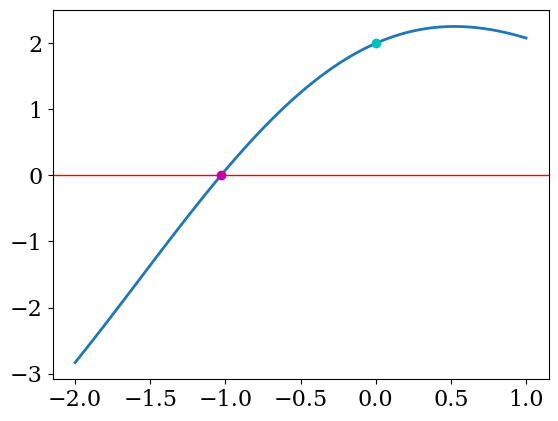
X=linspace(-2,1,100)
plt.plot(X,F(X),lw=2)
plt.plot(x0,F(x0),'co')
plt.plot(xe,F(xe),'mo')
plt.axhline(y=0,color='r',lw=1)
# racine
x1=fsolve(F,x0,fprime=dF)
print("racine=",x1,"erreur=",F(x1))
# sortie detaillee
[x1,infodict,ierr,mesg]=fsolve(F,x0,fprime=dF,full_output=True)
print("nbre d evaluation de F : ",infodict['nfev'])
# idem mais sans utiliser la dérivée (estimation par differences finies)
x1=fsolve(F,x0)
print("racine=",x1,"erreur=",F(x1))
[x1,infodict,ierr,mesg]=fsolve(F,x0,full_output=True)
print("nbre d evaluation de F: ",infodict['nfev'])
racine= [-1.02986653] erreur= [0.]
nbre d evaluation de F : 11
racine= [-1.02986653] erreur= [0.]
nbre d evaluation de F: 12
12.4.1. Exercice d’application#
Un projectile de masse \(M\) est tiré avec un angle \(\alpha\) et une vitesse initiale \(U_0\). En tenant compte de la résistance de l’air qui exerce une force proportionnelle à la vitesse \(F=K U\), la trajectoire du projectile est donnée par:
avec \(C=M/K\). Écrire un programme python permettant de calculer le temps et la distance du point d’impact.
AN: \(\alpha=45°\), \(U_0=40 m/s\)
12.5. Polynômes#
soit le polynôme \(P(x)\) de degré \(n\)
Pour évaluer ce polynôme, on peut programmer direction la relation précédente:
def EvalPoly(X,A):
""" evaluation du polynôme de coefficient A[i] en x """
somme = zeros(size(X))
for i,a in enumerate(A):
somme = somme + a*X**i
return somme
#
A=array([1.,2.,3.,4.])
X=array([1.0,-1.,2.,-2.])
print(EvalPoly(X,A))
A=2*random.rand(20)-1.
X=2*random.rand(100)-1.
%timeit EvalPoly(X,A)
[ 10. -2. 49. -23.]
98 μs ± 752 ns per loop (mean ± std. dev. of 7 runs, 10,000 loops each)
Pour évaluer \(P(x)\) on peut aussi utiliser la forme factorisée de Hörner, en récrivant \(P(x)\)
def Horner(X,A):
""" evaluation du polynôme de coefficient A[i] en x par l'algorithme de Horner"""
somme = zeros(size(X))
for a in reversed(A):
somme = X*somme + a
return somme
#
A=array([1.,2.,3.,4.])
X=array([1.0,-1.,2.,-2.])
print(Horner(X,A))
A=2*random.rand(20)-1
X=2*random.rand(100)-1.
%timeit Horner(X,A)
[ 10. -2. 49. -23.]
28.7 μs ± 91.9 ns per loop (mean ± std. dev. of 7 runs, 10,000 loops each)
La formule factorisée de Hörner est donc beaucoup plus efficace!! C’est celle utilisée dans la bibliothéque numpy
from numpy.polynomial.polynomial import polyval
A=array([1.,2.,3.,4.])
X=array([1.0,-1.,2.,-2.])
print(polyval(X,A))
A=2*random.rand(20)-1
X=2*random.rand(100)-1.
%timeit polyval(X,A)
[ 10. -2. 49. -23.]
34.2 μs ± 116 ns per loop (mean ± std. dev. of 7 runs, 10,000 loops each)
12.6. Interpolation#
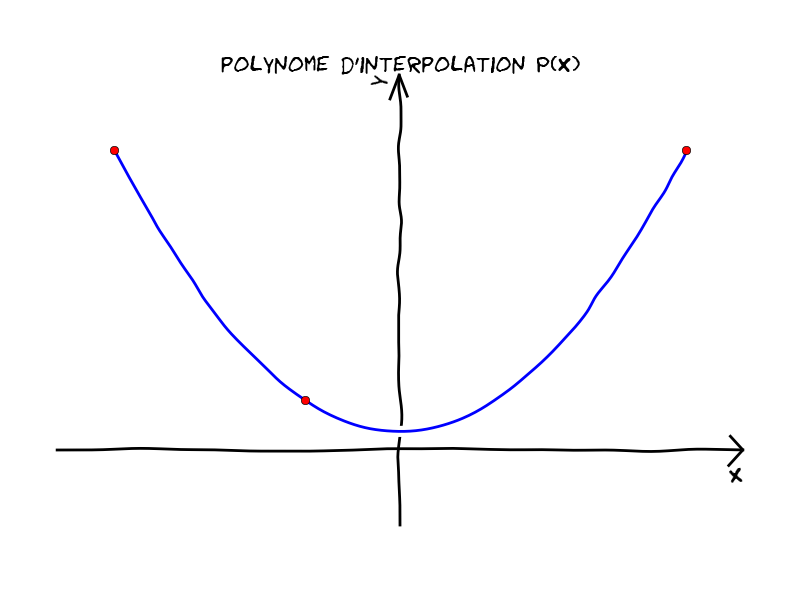
12.6.1. Interpolation de Lagrange#
Soient \(N+1\) points \(\left\{ X_i,Y_i \right\}_{i=0..N}\), le polynôme d’interpolation de Lagrange est le polynôme de degré \(N\) passant par ces \(N+1\) points.
12.6.2. Formule de Lagrange (instable si \(N>10\))#
# bibliotheque scipy
scipy.interpolate.lagrange
12.6.3. Pour \(N\) grand: interpolation locale (linéaire, spline, ..)#
# bibliotheque scipy
scipy.interpolate.interp1d
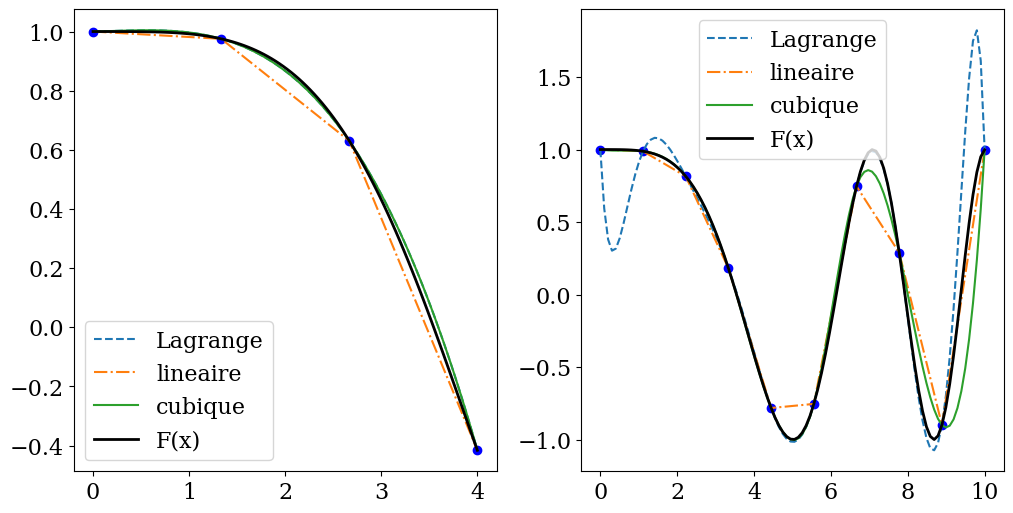
from scipy.interpolate import lagrange,interp1d
# fonction a interpoler
F=lambda x:cos(x**2/8.)
# interpolation sur 4 points
Xp1=linspace(0,4,4)
Yp1=F(Xp1)
X1=linspace(0,4,100)
P =lagrange(Xp1,Yp1)
P1=interp1d(Xp1,Yp1)
P3=interp1d(Xp1,Yp1,'cubic')
# puis sur 10 points
Xp2=linspace(0,10,10)
Yp2=F(Xp2)
X2=linspace(0,10,100)
Q =lagrange(Xp2,Yp2)
Q1=interp1d(Xp2,Yp2)
Q3=interp1d(Xp2,Yp2,'cubic')
# tracer
plt.figure(figsize=(12,6))
plt.subplot(1,2,1)
plt.plot(Xp1,Yp1,"bo")
plt.plot(X1,P(X1),'--',label="Lagrange")
plt.plot(X1,P1(X1),'-.',label="lineaire")
plt.plot(X1,P3(X1),'-',label="cubique")
plt.plot(X1,F(X1),'k-',lw=2,label="F(x)")
plt.legend(loc=0)
plt.subplot(1,2,2)
plt.plot(Xp2,Yp2,"bo")
plt.plot(X2,Q(X2),'--',label="Lagrange")
plt.plot(X2,Q1(X2),'-.',label="lineaire")
plt.plot(X2,Q3(X2),'-',label="cubique")
plt.plot(X2,F(X2),'k-',lw=2,label="F(x)")
plt.legend(loc=0)
<matplotlib.legend.Legend at 0x7f16361a8820>
12.6.4. Droite des moindres carrées#
Soient \(n\) couples de points expérimentaux: \((X_i,Y_i)_{i=0,n-1}\), on cherche à lisser ces points par la droite des moindres carrés: \(y = a x +b \)
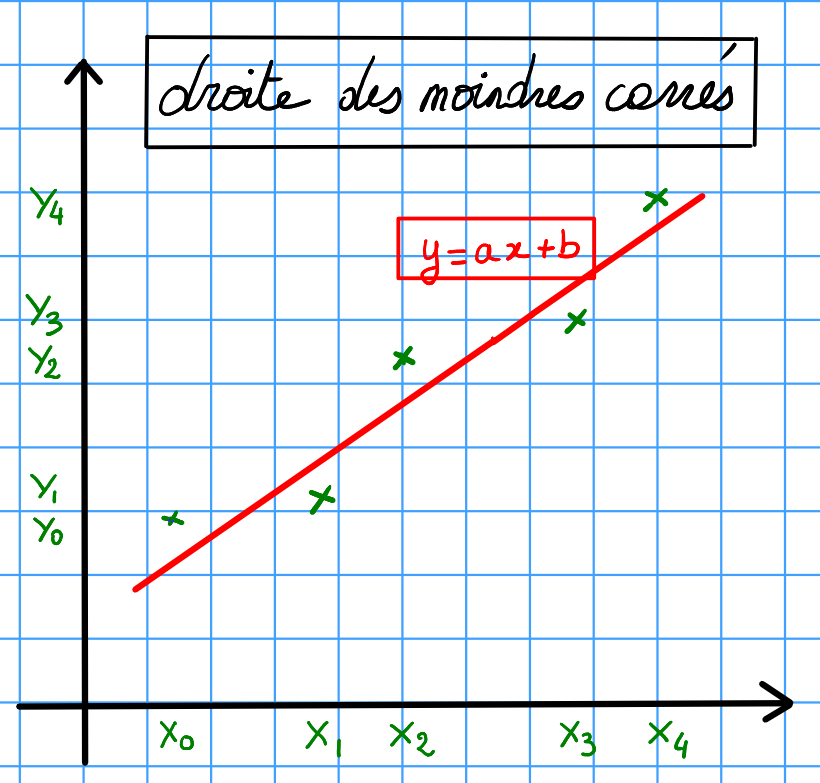
Principe
on détermine la droite \(y = a x + b\) qui minimise l’erreur \(Err\) entre les points de mesure et les points de la droite:
où \(\Delta_i ^2 = (a X_i +b - Y_i)^2\) représente le carré de l’erreur entre un point de mesure \((X_i,Y_i)\) et le point correspondant de la droite \((X_i, a X_i + b)\)
Les valeurs de \(a\) et \(b\) sont déterminées en minimisant l’erreur \(Err(a,b)\) par rapport à \(a\) et \(b\), i.e. tel que \(\frac{\partial Err}{\partial a} = 0 \) et \(\frac{\partial Err}{\partial b} = 0\)
On obtient ainsi le système linéaire de 2 équations:
dont la solution s’écrit:
12.7. Intégration#
formule de quadrature par approximation de la fonction \(f(x)\) par un polynôme d’interpolation \(P(x)\)
12.7.1. méthode des trapèzes (P(x) polynôme de degré 1 par morceaux)#
méthode d’ordre 2: erreur \(O(h^2)\)
# librairie scipy
scipy.integrate.cumtrapz
12.7.2. méthode de Simpson (P(x) polynôme de degré 2 par morceaux)#
méthode d’ordre 4: erreur \(O(h^4)\)
# librairie scipy
scipy.integrate.simps
12.7.3. méthode de Gauss#
on utilise des points de Gauss comme points d’interpolation
avec \(N\) points de Gauss, formule exacte pour des polynômes de degré \(\leq 2n+1\)
très précise pour \(f(x)\) analytique
# bibliotheque scipy scipy.integrate.quadrature
12.7.4. Comparaison des méthodes#
Calcul de \(I = \int_0^\pi \sin x\, dx = 2\)
def Simpson(Y,dx):
""" Calcul de l'integrale par la mehode de simspon
Y valeurs de f(x) en 2N+1 points distants de dx """
somme = 0.
N = size(Y)//2
for i in range(N):
somme = somme + Y[2*i+2]+4*Y[2*i+1]+Y[2*i]
return somme*dx/3.
#
N=20
X=linspace(0,pi,2*N+1)
dx=X[1]-X[0]
Y=sin(X)
print("Simpson=",Simpson(Y,dx))
# libaririe
from scipy.integrate import simps,cumtrapz
print("simps=",simps(Y,dx=dx))
print("trapz=",cumtrapz(Y,dx=dx)[-1])
# Gauss
from scipy.integrate import quadrature
print("Gauss=",quadrature(sin,0,pi,maxiter=7))
Simpson= 2.0000004230931827
---------------------------------------------------------------------------
ImportError Traceback (most recent call last)
Cell In[11], line 16
14 print("Simpson=",Simpson(Y,dx))
15 # libaririe
---> 16 from scipy.integrate import simps,cumtrapz
17 print("simps=",simps(Y,dx=dx))
18 print("trapz=",cumtrapz(Y,dx=dx)[-1])
ImportError: cannot import name 'simps' from 'scipy.integrate' (/home/buffat/venvs/jupyter/lib/python3.10/site-packages/scipy/integrate/__init__.py)
12.8. Equations différentielles#
12.8.1. Equation différentielle du 1er ordre#
\(Y(t)\) est une courbe dont l’équation donne la tangente
calcul de la trajectoire à partir de la vitesse
approximation de \(\frac{d Y}{d t}\) par différences finies
12.8.2. Méthode de Runge Kutta d’ordre 2#
approximation de la tangente au milieu de l’intervalle
méthode d’ordre 2
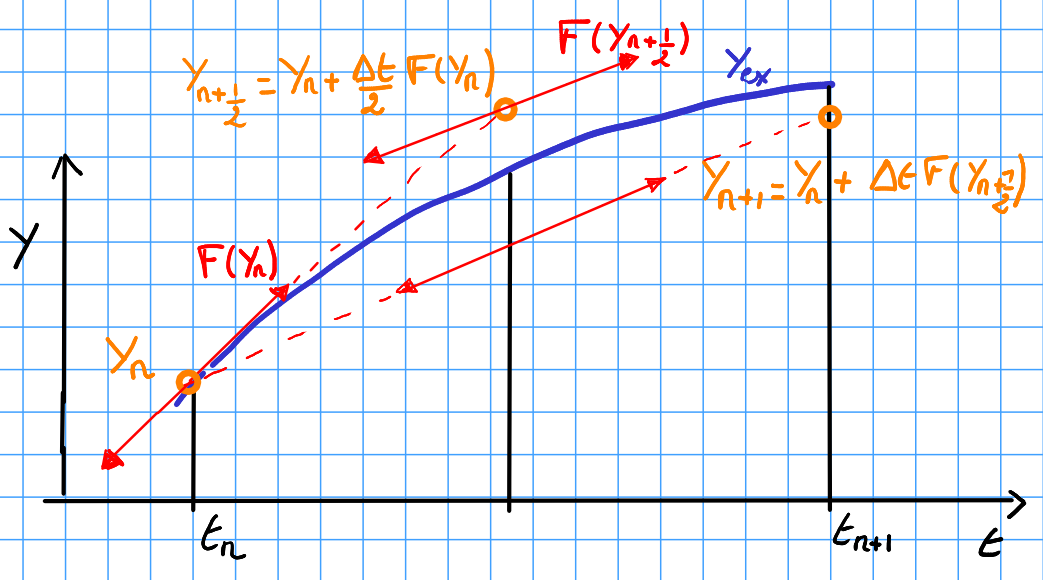
def RungeKutta2(F,Y0,t0,dt):
""" integration par RK2 de dY/dt=F(t,Y) de t0 a t0+dt avec Y(t0)=Y0 """
return Y0 + dt*F(t0 + dt/2. ,Y0 + dt/2.*F(t0,Y0))
utilisation bibliotheque scipy
import scipy
# Bibliothéque scipy.integrate.ode
nom='dopri5'
methode = scipy.integrate.ode(F).set_integrator(nom)
# nom = methode d'integration
# 'dopri5' methode Runge Kutta d'ordre 4(5)
# 'lsoda' methode implicite (Adams Bashford et BDF)
methode.set_initial_value(Y0,t0)
methode.integrade(t)
12.8.3. exemple: intégration de dY/dt = Y avec Y(0)=1#
solution \(Y(t)=e^t\)
from numpy import *
import matplotlib.pyplot as plt
from scipy.integrate import ode
# second membre EDO
def F(t,Y):
return Y
# parametres
t0 = 0.; Y0 = 1.
tf = 2.; N = 10
T=linspace(t0,tf,N)
# methode RK2
Y2=zeros(N)
Y2[0]=Y0
Yex = exp(T)
dt=T[1]-T[0]
for i in range(1,N):
Y2[i] = RungeKutta2(F,Y2[i-1],T[i-1],dt)
# scipy ode
Y4=zeros(N)
Y4[0]=Y0
RK45=ode(F).set_integrator('dopri5')
RK45.set_initial_value(Y0,t0)
for i in range(1,N):
Y4[i]=RK45.integrate(T[i])
# tracer
plt.figure(figsize=(12,6))
plt.subplot(1,2,1)
plt.plot(T,Y2,'o',label="RK2")
plt.plot(T,Y4,'v',label="RK45")
plt.plot(T,Yex)
plt.title('solution dY/dt=Y')
plt.legend(loc=0)
plt.subplot(1,2,2)
plt.plot(T,abs(Y2-Yex),'o',label="RK2")
plt.plot(T,abs(Y4-Yex),'v',label="RK45")
plt.title('Erreur')
plt.legend(loc=0)
plt.show()
12.8.4. Equation différentielle du second ordre#
transformation en un système EDO d’ordre 1:
on pose \(Y_1 = y\) et \(Y_2 = \frac{dy}{dt}\)
12.8.5. Méthode de Verlet (1967)#
Intégration de l” équation du mouvement en astrophysique et dynamique moléculaire
Equation de Newton avec des forces \(F\) dépendants de la position \(X(t)\)
Approximation centrée d’ordre 2 de la dérivée seconde
**Algorithme de Verlet **
erreur d’ordre 4, simplectique pour les systèmes Hamiltonien (conservatif)
démarrage des itérations (ordre 3)
12.8.6. exemple: trajectoire de la terre autour du soleil#
loi de la gravitation universelle: planete masse \(m\) distante de \((x,y)\) d’un soleil masse \(M\):
from numpy import *
import matplotlib.pyplot as plt
from scipy.integrate import ode
# unites astronomiques
LONG=1.e11
MASSE=1.e24
JOUR=24.*3600
# constante
G=6.67e-11/(LONG**3/MASSE/JOUR**2) # constante de gravitation en m^3/kg/s^2
M=2.0e30/MASSE # masse du soleil en kg
m=6.0e24/MASSE # masse de la terre en kg
r0=147.0e9/LONG # distance initiale terre soleil en m
u0=30.4e3*JOUR/LONG # vitesse initiale en m/s
# nbre de jours d'integration
N=365
# integration avec la methode de verlet
# =====================================
# calcul force attraction
def Force(x,y):
r=sqrt(x*x+y*y)
return G*M/r**3
#
t=linspace(0,N-1,N)
x=zeros(N); x[0]=r0
y=zeros(N); y[0]=0
# pas d'integration par jour
npj=20
dt=1./npj
# position initiale a t=t0 et t=t0-dt
x1=r0; y1=0.; a0 = 0.5*Force(x1,y1)*dt**2
x0 = x1 -a0*x1
y0 = y1 - u0*dt -a0*y1
# boucle d'integration
for i in range(1,N):
for k in range(npj):
a1 = Force(x1,y1)*dt**2
x2 = 2*x1 - x0 -a1*x1
y2 = 2*y1 - y0 -a1*y1
x0=x1; y0=y1
x1=x2; y1=y2
x[i]=x2
y[i]=y2
# integration avec RK45
# =====================
# second membre ODE d'ordre 1
def F(t,Y):
r = sqrt(Y[0]*Y[0]+Y[1]*Y[1])
a = G*M/r**3
return [Y[2], Y[3], -a*Y[0], -a*Y[1]]
# scipy ode RK45
t4=linspace(0,N-1,N)
x4=zeros(N); x4[0]=r0
y4=zeros(N); y4[0]=0
Y0=array([r0,0,0,u0])
RK45=ode(F).set_integrator('dopri5')
RK45.set_initial_value(Y0,0.)
for i in range(1,N):
[x4[i],y4[i],u4,v4]=RK45.integrate(t4[i])
# tracer
plt.figure(figsize=(12,6))
plt.subplot(1,2,1)
plt.plot(x,y,label='verlet')
plt.plot(x4,y4,label='rk45')
plt.plot(0.,0.,'o')
plt.legend(loc=0)
plt.title("Trajectoire")
plt.axis('equal')
plt.subplot(1,2,2)
plt.plot(t4,sqrt(x**2+y**2)-sqrt(x4**2+y4**2))
plt.title("Difference")
plt.show()
12.9. Exercices#
12.9.1. Swinging pendulum#
On considère le mouvement de \(N\) pendules simples de longueurs \(L\) variables.
Écrire un programme python qui calcule le mouvement de ces pendules. Déterminez la répartition des longueurs \(L\) permettant d’obtenir le type de mouvement ci-dessous avec \(N=15\) pendules.
On comparera aussi le résultat avec les vidéos d’expériences trouvées sur le net.
from anim import trace_swing_pendulum
HTML(trace_swing_pendulum())
12.9.2. pendule simple avec une corde souple#
On considère les oscillations d’un pendule simple fixé à une corde souple de longueur maximum L et de masse négligeable par rapport au pendule. Lorsque la longueur de la corde est maximum, elle peut exercer uniquement une force de tension centripète sur la masse m du pendule. Le pendule est lancé avec une vitesse initiale, et commence à osciller. Si la tension dans le fil devient nulle, le pendule est alors soumis uniquement à la force de gravité et sa trajectoire devient parabolique. Lors que cette trajectoire intercepte le cercle de longueur l, un choc se produit puisque le fil atteint alors sa longueur maximum et exerce à nouveau une tension sur le pendule. Ce choc est un choc mou avec perte d’énergie, et l’on suppose que ce choc est telle que la vitesse tangentielle se conserve et la vitesse normale s’annule. Le pendule se met alors à osciller, mais avec des oscillations de plus faibles amplitudes.
Ecrire un programme python qui calcule la trajectoire du pendule.
from anim import trace_pendulum
HTML(trace_pendulum())
12.9.3. problème à N corps#
On considère un système planétaire de \(N\) masses en interaction gravitationnelle. La force exercée par la masse \(m_i\) sur la masse \(m_j\) est donnée par la relation de Newton: $\( F_{i,j} = \frac{G m_i m_j}{r_{i,j}^2} \mbox{ avec } r_{i,j}=\mbox{distance entre les 2 masses}\)\( \)G\( est la constante de gravitation universelle. Pour \)N=3$, on a le problème classique des 3 corps qui intrigue les physiciens depuis Newton.
Écrire un programme python calculant la trajectoire de \(N\) corps se trouvant dans un même plan, modélisant un système planétaire où la première masse représente le soleil et les autres masses les planètes.
Quelle est la complexité de l’algorithme en fonction de N ?
Dans le cas du système à trois corps Soleil-Terre-Jupiter, retrouver le mouvement du système solaire.
unités: Dans le système d’unités astronomiques, i.e. la distance \(L_t=1.49\,10^{11}\,m\) de la terre au soleil comme unité de longueur, la masse \(M_t=6\,10^{24}\,kg\) de la terre comme unité de masse, et l’année terrestre moyenne \(T_t=365,25\,jours\) comme unité de temps, on a \(G=0.00012\). On a aussi la masse du Soleil \(m_0=3.33\,10^5\), la masse de Jupiter \(m_2=316.7\) et la distance Soleil Jupiter \(r_2=5.2\).
Étudier le comportement du système lorsque la masse du soleil diminue.
Essayer de retrouver la solution périodique en huit découverte en 1993 par Christopher Moore.
from anim import trace_trois_corps
HTML(trace_trois_corps())
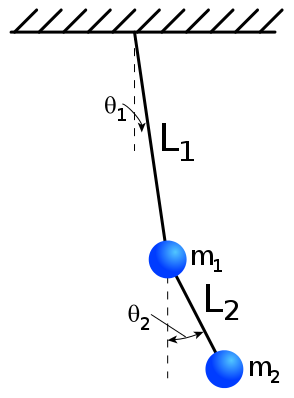
12.9.4. pendule double: mouvement chaotic#
On veut étudier le mouvement d’un double pendule par intégration des équations du mouvement.
Écrire un programme python pour calculer la position des 2 masses \(m_1\) et \(m_2\) au cours du temps.
On comparera la simulation aux vidéos d’expérience disponible sur le net.
from anim import trace_double_pendulum
HTML(trace_double_pendulum())
12.9.5. Évolution du volume d’une particule fluide#
En suivant la trajectoire d’une particule fluide dans un champ de vitesse \(U=[u(x,y),v(x,y)]\), on détermine la variation du volume $V(t) de la particule.
On veut vérifier la relation suivante:
Ecrire un programme python qui calcule la trajectoire \((x(t),y(t)\) d’une particule fluide:
et détermine la variation de son volume \(V(t)\)
from anim import trace_divergence
HTML(trace_divergence())
12.10. FIN de la leçon#

