Marc BUFFAT

Marc BUFFAT

Professeur au département de Mécanique, Lyon 1 e-mail

Blog scientifique et pédagogique utilisant des notebooks IPython et Linux

Cours Python scientifique

Table des matières

In [1]:
%matplotlib inline
%autosave 300
import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
from matplotlib import rcParams
rcParams['font.family'] = 'serif'
rcParams['font.size'] = 14
from IPython.core.display import HTML
from IPython.display import display
from matplotlib import animation
css_file = 'style.css'
HTML(open(css_file, "r").read())

Autosaving every 300 seconds
Out[1]:

Python scientifique (numpy)

Marc BUFFAT, dpt mécanique, Université Claude Bernard Lyon 1

Licence Creative Commons
Mise à disposition selon les termes de la Licence Creative Commons
Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 2.0 France.

Tableaux avec numpy

La bibliothéque Numpy implémente une gestion efficace des tableaux pour représenter les vecteurs et matrices

import numpy as np

  • tableau (array): ensemble ordonnée de valeurs de même type (entier, réel) accessible à partir d’un indice commencant à 0. La dimension d’un tableau est fixe.
  • liste (list): ensemble ordonnée de valeurs pas forcement du même type. La dimension d’une liste est variable.

Différences entre tableaux et listes

In [2]:
# tableau
X=np.array([1.,2,3.0])
X[0]=0
print(" X=",X)
# liste
Y=[1.,2,3.0]
Y[0]=0
print(" Y=",Y)
# ajout d'un élément 
Y.append('quatre')
print("Y=",Y)
# dimension de X
print("nbre de dimension =",X.ndim)
print("taille en octets de X = ",X.nbytes," taille elt=",X.itemsize)

 X= [ 0.  2.  3.]
 Y= [0, 2, 3.0]
Y= [0, 2, 3.0, 'quatre']
nbre de dimension = 1
taille en octets de X =  24  taille elt= 8
In [3]:
# tableau en 2D
X=np.array([[1.,2.],[3.,4]],dtype=np.float64)
print("X=",X)
print("dim X=",X.shape,X.size)
# liste de liste
Y=[[1.,2.],[3,4]]
print("Y=",Y)
print("dim Y=",len(Y),len(Y[0]),len(Y[1]))

X= [[ 1.  2.]
 [ 3.  4.]]
dim X= (2, 2) 4
Y= [[1.0, 2.0], [3, 4]]
dim Y= 2 2 2

Comparaison création

On peut représenter des vecteurs et tableaux avec des listes mais c’est très inefficace!!!

In [4]:
# creation tableau de N elts
def creationTab(N):
    T=np.zeros((N),dtype=np.int64)
    return T
N=10000
%timeit creationTab(N)

7.96 µs ± 83.5 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)
In [5]:
# creation liste de N elts
def creationList(N):
    L=[0]*N
    return L
N=10000
%timeit creationList(N)

30.6 µs ± 111 ns per loop (mean ± std. dev. of 7 runs, 10000 loops each)

Créations de tableaux

  • avec la fonction array

      X=np.array(object,dtype=type)
  X=np.array(list,dtype=type)

    object = un tableau ou equivalent

    list = une liste de valeurs

    type = type des elements

    int float complex bool 
np.int32, np.int64, np.float32, np.float54, np.complex128

    • avec des fonction de numpy

      • sans initialisation des valeurs 
          X=np.empty(shape)
        shape = liste des dimensions entre () (tuple)

      • initialisation valeurs constante nulle ou #0

           X=np.zeros(shape,dtype)
   X=np.ones(shape,dtype)

      • intervalle de valeurs

           X=np.arange(deb,fin,pas)
   X=np.linspace(xdeb,xfin,nb_de_points)

      • meshgrid en dimension >= 2D

           X,Y=np.meshgrid(X0,Y0)

      • random

           X=np.random.random(shape)
In [6]:
# creation de tableaux
print(2*np.ones((3,2)))
print(np.arange(0.,1.,0.1))
print(np.linspace(0.,1.,11))
X,Y=np.meshgrid(np.linspace(0,1,3),np.linspace(0,1,2))
print("X=",X)
print("Y=",Y)
print("Valeurs aleatoires entre 0 et 1 =",np.random.random((5)))

[[ 2.  2.]
 [ 2.  2.]
 [ 2.  2.]]
[ 0.   0.1  0.2  0.3  0.4  0.5  0.6  0.7  0.8  0.9]
[ 0.   0.1  0.2  0.3  0.4  0.5  0.6  0.7  0.8  0.9  1. ]
X= [[ 0.   0.5  1. ]
 [ 0.   0.5  1. ]]
Y= [[ 0.  0.  0.]
 [ 1.  1.  1.]]
Valeurs aleatoires entre 0 et 1 = [ 0.24781711  0.00580408  0.61227092  0.97760247  0.24224229]

  • initialisation avec des listes de compréhension

     X = np.array([ val for i in range(n)])
In [7]:
print(np.array([i*i for i in range(10)]))

[ 0  1  4  9 16 25 36 49 64 81]

Indicage des tableaux

on compte à partir de 0 (comme en algorithmique)

  • X[0+i] élément i+1 de i

  • X[-1] dernier element de i = X[n-1]

  • X[-1-j] j élément avant le dernier = X[n-j]

  • X[i:j:pas] coupe ou slice du tableau X[i],X[i+pas],X[i+2p], .. X[k] avec k<j

In [8]:
X=np.array([j**3 for j in range(10)])
print(X)
print(X[0],X[1],X[2],X[-3],X[-2],X[-1])
print(X[-2:-1])

[  0   1   8  27  64 125 216 343 512 729]
0 1 8 343 512 729
[512]

Adressage indirecte (fancy adressing)

on utilise des tableaux d’indices rol et col

    A[row,col]
In [9]:
A = np.array([[n+m*10 for n in range(5)] for m in range(5)])
print("A=",A)
row_indices=[0,2]
print("[A[i=0,2,:]]=\n",A[row_indices])
col_indices = [1, -1]
print("[A[0,1],A[2,-1]]=",A[row_indices,col_indices])

A= [[ 0  1  2  3  4]
 [10 11 12 13 14]
 [20 21 22 23 24]
 [30 31 32 33 34]
 [40 41 42 43 44]]
[A[i=0,2,:]]=
 [[ 0  1  2  3  4]
 [20 21 22 23 24]]
[A[0,1],A[2,-1]]= [ 1 24]
  • utilisation de la fonction np.ix_ pour sélectionner des sous-matrices
In [10]:
print("sous matrice= ",A[np.ix_(row_indices,col_indices)])

sous matrice=  [[ 1  4]
 [21 24]]
  • masque avec des valeurs logiques (bool)
    • utile pour sélectionner les valeurs d’un vecteur dans un intervalle
In [11]:
B = np.linspace(0.,1.,5)
print("B=",B)
mask = np.array([True, False, False,True, True])
print(B[mask])
mask=(B>0.2)*(B<0.8)
print(B[mask])

B= [ 0.    0.25  0.5   0.75  1.  ]
[ 0.    0.75  1.  ]
[ 0.25  0.5   0.75]

Aliasing

In [12]:
print("pas d'aliasing avec les scalaires")
x=2
y=x
x=3
print(x,"#",y)

pas d'aliasing avec les scalaires
3 # 2
In [13]:
print("mais aliasing avec les listes et tableaux")
X=[1,2,3]
Y=X
X[0]=0
print(X,"==",Y)

mais aliasing avec les listes et tableaux
[0, 2, 3] == [0, 2, 3]

utilisation de la fonction copy (explicite ou implicite)

In [14]:
print("pas d'aliasing si copie explicite des valeurs")
X=np.array([1,2,3])
Y=X.copy()
X[0]=0
print(X,Y)
Y=np.zeros(X.shape)
Y[:]=X
X[0]=3
print(X,Y)

pas d'aliasing si copie explicite des valeurs
[0 2 3] [1 2 3]
[3 2 3] [ 0.  2.  3.]

Notation matricielle

  • Attention par defaut opération sur les éléments
  • les fonctions mathématiques dans numpy ont pour aguments des tableaux
  • np.dot produit scalaire np.outer produit tensorielle np.inner
In [15]:
X=np.arange(0,3,1)
print("cos(X)=",np.cos(X))
print("X*X=",X*X)
print("X.X=",np.dot(X,X))
print("XoX=\n",np.outer(X,X))
print("XiX=",np.inner(X,X))

cos(X)= [ 1.          0.54030231 -0.41614684]
X*X= [0 1 4]
X.X= 5
XoX=
 [[0 0 0]
 [0 1 2]
 [0 2 4]]
XiX= 5
In [16]:
A=np.array(np.outer(np.arange(3),np.arange(3)))
print(type(A),A.shape)
print("A*X=\n",A*X)
print("A.X=\n",np.dot(A,X))
print("AoX=\n",np.outer(A,X))
print("AiA=\n",np.inner(A,A))
print("A.At=\n",np.dot(A,A.transpose()))

<class 'numpy.ndarray'> (3, 3)
A*X=
 [[0 0 0]
 [0 1 4]
 [0 2 8]]
A.X=
 [ 0  5 10]
AoX=
 [[0 0 0]
 [0 0 0]
 [0 0 0]
 [0 0 0]
 [0 1 2]
 [0 2 4]
 [0 0 0]
 [0 2 4]
 [0 4 8]]
AiA=
 [[ 0  0  0]
 [ 0  5 10]
 [ 0 10 20]]
A.At=
 [[ 0  0  0]
 [ 0  5 10]
 [ 0 10 20]]

attention:

  • on évite les boucles explicites pour des questions d’efficacité
  • mais on commence toujours par écrire la forme explicite avec des boucles , puis ensuite la forme vectorielle

exemple: calcul de la forme quadratique $$ \Phi = \sum_{i=1}^n \sum_{j=1}^n A_{ij} X_i X_j - \sum_{j=1}^n B_j X_j$$

In [17]:
# calcul explicite
Phi=0.0
n=X.size
B=np.ones(X.shape)
for i in range(n):
    sum=0.0
    for j in range(n):
        sum = sum + A[i,j]*X[j]
    Phi = Phi + (sum - B[i])*X[i]
print(Phi)

22.0
In [18]:
# fonction numpy
print(np.dot(np.dot(A,X)-B,X))

22.0

calcul du résidu d’un système linéaire

$$R = B - A X$$$$R_i = B_i - \sum_{i=1}^n A_{ij} X_j$$

ATTENTION: problème dans le code suivant.

trouver l'erreur!!!!!!!

In [19]:
n=5
B=np.random.random((n))
A=np.random.random((n,n))
X=np.random.random((n))
# calcul avec notation matricielle
R  = B
R -= np.dot(A,X)
print("|R|=",np.linalg.norm(R))
# 2ne version
R = B - np.dot(A,X)
print("|R|=",np.linalg.norm(R))

|R|= 1.88647149608
|R|= 4.24336660456
In [20]:
# calcul explicite
R=np.zeros((n))
for i in range(n):
    R[i]=B[i]
    for j in range(n):
        R[i] = R[i] - A[i,j]*X[j]
print("|R|=",np.linalg.norm(R))

|R|= 4.24336660456

erreur: problème aliasing

    R[:]=B

Analyse de données d’un tableau

    np.amax(tab)    max suivant un axe
    np.amin(tab)    min
    np.mean(tab)    moyenne
    np.sum(tab)     somme
    np.prod(tab)    produit
In [21]:
M=np.random.random((3,3))
print("M=",M)

M= [[ 0.625944    0.3247767   0.96875731]
 [ 0.32931559  0.0709186   0.0203493 ]
 [ 0.10922643  0.3532391   0.35236728]]
In [22]:
print("max=",np.amax(M))
print("min=",np.amin(M,axis=1))
print("moy=",np.mean(M,axis=0))
print("sum=",np.sum(M))
print("prod=",np.prod(M,axis=0))

max= 0.968757308429
min= [ 0.3247767   0.0203493   0.10922643]
moy= [ 0.35482867  0.2496448   0.44715796]
sum= 3.15489430507
prod= [ 0.02251518  0.00813605  0.00694641]

Lecture / Ecriture des données

gestion de fichiers classique avec Python

F=open("nom fichier","r")
L=F.readlines()
# decodage de chaque ligne
F.close()

lecture de données (format texte en colonnes)

A=np.loadtxt("nom de fichier")

ecriture d’un tableau de données

np.savetxt("nom de fichier",A)

ATTENTION utilisation de savetxt avec une variable fichier (File Handle):

  • ouverture avec ‘wb’ (binary write)

Exemple: lecture fichier de données

In [23]:
%%bash
cat data/donnee.dat

# cas alpha= 0.783841
2.28163 9.54997
1.38177 6.44183
2.68774 10.8512
1.3478 6.31609
1.34159 6.29375
In [24]:
# methode classique de lecture
F=open("data/donnee.dat","r")
L=F.readlines()
F.close()
# traitement des donnees
N=len(L)-1
X=np.zeros((N))
Y=np.zeros((N))
for i in range(N):
    line = L[i+1].split()
    X[i] = float(line[0])
    Y[i] = float(line[1])
print("X=",X)
print("Y=",Y)

X= [ 2.28163  1.38177  2.68774  1.3478   1.34159]
Y= [  9.54997   6.44183  10.8512    6.31609   6.29375]
In [25]:
# version avec loadtxt
A=np.loadtxt("data/donnee.dat")
X=A[:,0]
Y=A[:,1]
print("X=",X)
print("Y=",Y)

X= [ 2.28163  1.38177  2.68774  1.3478   1.34159]
Y= [  9.54997   6.44183  10.8512    6.31609   6.29375]

Exemple: écriture fichier de données

In [26]:
A=np.random.rand(5,4)
F=open("data/data1.dat","w")
F.write("# fichier de resultat\n")
for i in range(A.shape[0]):
    for j in range(A.shape[1]):
        F.write("{0:8.4f} ".format(A[i,j]))
    F.write("\n")
F.close()
In [27]:
# version avec savetxt
F=open("data/data2.dat","wb")
F.write("# fichier de resultat\n".encode('utf-8'))
np.savetxt(F,A)
F.close()
In [28]:
%%bash
cat data/data1.dat
cat data/data2.dat

# fichier de resultat
  0.4781   0.7973   0.9088   0.7957 
  0.4313   0.1692   0.4706   0.4839 
  0.6980   0.0454   0.4592   0.4355 
  0.2742   0.2562   0.8662   0.8665 
  0.1383   0.4682   0.3033   0.8004 
# fichier de resultat
4.780642346487723460e-01 7.972658915555631554e-01 9.088277338939448891e-01 7.956591332368184721e-01
4.313016887675840128e-01 1.691594773660001216e-01 4.705839544393131124e-01 4.839450605562675145e-01
6.980155886575257762e-01 4.543995600070638297e-02 4.591764447201823751e-01 4.354773379702492342e-01
2.741837117426068060e-01 2.561743225273549474e-01 8.661625105586603368e-01 8.664581270631726007e-01
1.383022268771603169e-01 4.681933679738564669e-01 3.032914578314416243e-01 8.003531174556696159e-01

Affichage avec un format ( printf en C)

print "format "%(val1,val2)

dans la chaine format : %d (decimal) %f (flottant) %s (chaine)

avec python 3:

print("x={},y={}".format(val1,val2))

print("x={1:fmt},y={0:fmt}".format(val2,val1))

avec pos (position) p.e. 0 1 et fmt (format) p.e. 8g 8f 8e

In [29]:
print("Pi=",np.pi)
print("Valeur approchée de Pi=%5.3f"%np.pi)
print("Valeur approchée de Pi={:5.2f}".format(np.pi))

Pi= 3.141592653589793
Valeur approchée de Pi=3.142
Valeur approchée de Pi= 3.14

Bibliothèque SCIPY

La bibliothéque SciPy (Scientifique Python) est basée sur Numpy et sa gestion efficace des tableaux multi-dimensionnels. Elle comprends entre autre des algorithmes pour:

utilisation

     import scipy as sp

ou import scipy.integrate as sint ou from scipy.intrate import ode

Fonctions spéciales

Fonctions de Bessel

Equivalent des fonctions trigonométriques sinus et cosinus en coordonnéees polaires

In [30]:
# fonction de Bessel de 1ere especes
from scipy.special import jn, jn_zeros
In [31]:
X=np.linspace(0,10,100)
plt.plot(X,jn(0,X),label="$J_0$")
plt.plot(X,jn(1,X),label="$J_1$")
plt.plot(X,jn(2,X),label="$J_2$")
plt.legend(loc=0)
Out[31]:
<matplotlib.legend.Legend at 0x7fd884068f28>
In [32]:
print("Zeros de Jn(1)=",jn_zeros(1,5))

Zeros de Jn(1)= [  3.83170597   7.01558667  10.17346814  13.32369194  16.47063005]

Polynômes (Chebyshev, Legendre, Laguerre, Hermite,..)

import numpy.polynomial.chebyshev as cheb

Intégration

Quadrature: calcul d’une valeur approchée

$$ I = \int_a^b f(x) dx$$
In [33]:
from scipy.integrate import quad
def f(x):
    return np.cos(x)
Ih,err=quad(f,0,np.pi/2)
print("Integrale =",Ih," Erreur =",err)

Integrale = 0.9999999999999999  Erreur = 1.1102230246251564e-14

équations différentielles ordinaires (ODE)

  • Forme standard vectorielle avec $Y=[y_1,y_2,…y_n]$ avec une CI: $Y(0)=Y_0$ $$ Y’ = F(Y,t) $$

  • Pour une ODE d’ordre n, changement de variables: $$ y_1 = y, y_2 =y’,… y_n = y^{(n-1)}$$

Mouvement du pendule double

Voir le detail sur [http://en.wikipedia.org/wiki/Double_pendulum]

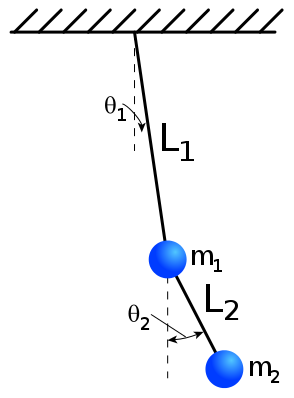
  • Equation du mouvement (2 ddl, EDO d’ordre 2)

cas $L_1=L_2=l$ et $m_1=m_2=m$

Lagrangien 2 ddl

$$\begin{eqnarray}L(\theta_1,\theta_2,\dot{\theta_1},\dot{\theta_2},t) &=& \frac{ml^2}{6}[\dot{\theta_2}^2+4\dot{\theta_1}^2+3\dot{\theta_1}\dot{\theta_2}\cos(\theta_1-\theta_2)]\& + &\frac{mgl}{2}(3\cos\theta_1+\cos\theta2))\end{eqnarray}$$

En posant $p_{\theta_1} =\frac{\partial L}{\partial \theta_1}$ et $p_{\theta_2} =\frac{\partial L}{\partial \theta_2}$ les quantités de mouvement généralisées, les équations de Lagrange s’écrivent

${\dot p_{\theta_1}} = -\frac{1}{2} m \ell^2 \left [ {\dot \theta_1} {\dot \theta_2} \sin (\theta_1-\theta_2) + 3 \frac{g}{\ell} \sin \theta_1 \right ]$

${\dot p_{\theta_2}} = -\frac{1}{2} m \ell^2 \left [ -{\dot \theta_1} {\dot \theta_2} \sin (\theta_1-\theta_2) + \frac{g}{\ell} \sin \theta_2 \right]$

En utilisant la définition de $p_{\theta_1}$ et $p_{\theta_2}$

${\dot \theta_1} = \frac{6}{m\ell^2} \frac{ 2 p_{\theta_1} - 3 \cos(\theta_1-\theta_2) p_{\theta_2}}{16 - 9 \cos^2(\theta_1-\theta_2)}$

${\dot \theta_2} = \frac{6}{m\ell^2} \frac{ 8 p_{\theta_2} - 3 \cos(\theta_1-\theta_2) p_{\theta_1}}{16 - 9 \cos^2(\theta_1-\theta_2)}.$

  • Changement de variable (4 ddl, 4 EDO d’ordre 1) $$x = [x_1=\theta_1, x_2=\theta_2, x_3=p_{\theta_1}, x_4=p_{\theta_2}]$$

${\dot x_1} = \frac{6}{m\ell^2} \frac{ 2 x_3 - 3 \cos(x_1-x_2) x_4}{16 - 9 \cos^2(x_1-x_2)}$

${\dot x_2} = \frac{6}{m\ell^2} \frac{ 8 x_4 - 3 \cos(x_1-x_2) x_3}{16 - 9 \cos^2(x_1-x_2)}$

${\dot x_3} = -\frac{1}{2} m \ell^2 \left [ {\dot x_1} {\dot x_2} \sin (x_1-x_2) + 3 \frac{g}{\ell} \sin x_1 \right ]$

${\dot x_4} = -\frac{1}{2} m \ell^2 \left [ -{\dot x_1} {\dot x_2} \sin (x_1-x_2) + \frac{g}{\ell} \sin x_2 \right]$

In [34]:
g = 9.82
L = 0.5
m = 0.1
def F(x, t):
    """ 2nd membre F(X) des équations ODE du pendule double """
    x1, x2, x3, x4 = x[0], x[1], x[2], x[3]
    
    dx1 = 6.0/(m*L**2) * (2 * x3 - 3 * np.cos(x1-x2) * x4)/(16 - 9 * np.cos(x1-x2)**2)
    dx2 = 6.0/(m*L**2) * (8 * x4 - 3 * np.cos(x1-x2) * x3)/(16 - 9 * np.cos(x1-x2)**2)
    dx3 = -0.5 * m * L**2 * ( dx1 * dx2 * np.sin(x1-x2) + 3 * (g/L) * np.sin(x1))
    dx4 = -0.5 * m * L**2 * (-dx1 * dx2 * np.sin(x1-x2) + (g/L) * np.sin(x2))
    
    return [dx1, dx2, dx3, dx4]
In [35]:
def Energie(x):
    """ calcul de l'energie totale du système """
    t1, t2, p1, p2 = x[0], x[1], x[2], x[3]
    dt1 = 6.0/(m*L**2) * (2 * p1 - 3 * np.cos(t1-t2) * p2)/(16 - 9 * np.cos(t1-t2)**2)
    dt2 = 6.0/(m*L**2) * (8 * p2 - 3 * np.cos(t1-t2) * p1)/(16 - 9 * np.cos(t1-t2)**2)
    Et = L**2/6*(4*dt1**2+dt2**2+3*dt1*dt2*np.cos(t1-t2)) - g*L/2*(3*np.cos(t1)+np.cos(t2))
    return Et
In [36]:
from scipy.integrate import odeint
# cdts initiale: cas petites oscillations
x0 = [np.pi/20, np.pi/20, 0, 0]
# calcul de la solution en n points sur l'intervalle 0 10s
t = np.linspace(0, 10, 1000)
# integration numérique 
x = odeint(F, x0, t, rtol=1.e-8,atol=1.e-10)
# coordonnees du pendule
x1 = + L * np.sin(x[:, 0])
y1 = - L * np.cos(x[:, 0])
x2 = x1 + L * np.sin(x[:, 1])
y2 = y1 - L * np.cos(x[:, 1])
# calcul energie totale
Et = [Energie(xi) for xi in x]
In [37]:
# tracer de la solution
plt.figure(figsize=(12,6))
plt.subplot(1,2,1)
plt.plot(t,x[:,0],lw=2,label="$\\theta_1$")
plt.plot(t,x[:,1],lw=2,label="$\\theta_1$")
plt.legend(loc=0)
plt.subplot(1,2,2)
plt.plot(x1,y1)
plt.plot(x2,y2)
plt.axis('equal')
plt.title('trajectoire')
Out[37]:
<matplotlib.text.Text at 0x7fd8550a6fd0>
In [38]:
# verification
plt.figure(figsize=(10,6))
plt.plot(t,Et,lw=2)
plt.title("E. totale")
Out[38]:
<matplotlib.text.Text at 0x7fd854fd1e80>

Transformation de Fourier

Analyse du signal $\theta_1$ et $\theta_2$ précédent pour mettre en évidence les 2 modes propres du système. Comparaison avec la fréquence du pendule simple.

In [39]:
from scipy.fftpack import fft,fftfreq
# FFT de theta1 et theta2
n2 = x.shape[0]//2
f1 = fft(x[:,0])
f2 = fft(x[:,1])
# plage de frequence
dt=t[1]-t[0]
w = fftfreq(len(t), dt)
# frequence de base
F0 = np.sqrt(g/L)/(2*np.pi)
In [40]:
plt.title("spectre")
plt.semilogy(w[:n2],abs(f1[:n2]),lw=2,label="$\\theta_1$")
plt.semilogy(w[:n2],abs(f2[:n2]),lw=2,label="$\\theta_2$")
plt.xlim(0,10)
plt.semilogy([F0,F0],[0.01,100.],'--k')
plt.legend()
Out[40]:
<matplotlib.legend.Legend at 0x7fd854fe9908>

Algèbre linéaire

Résolution système linéaire $A x = b$

     import scipy.linalg as lin
     lin.solve(A,B)    résolution AX=B
     lin.inv(A)        calcul inverse de A !!!
     lin.det(A)        déterminant de A
     lin.norm(A,ord=n) norme de A 

    A.conjugate()
    A.transpose()
    A.real
    A.imag
    M.max(axis=0)
    M.min()
    np.diag(A)
    np.trace(A)
In [41]:
n=2
A=np.random.random((n,n))
M = A + 1j*A.transpose()
print("conjugué\n",M.conjugate())
print("transpose (attention #)\n",M.transpose())
print("parti imaginaire\n",M.imag)
print("Diag A=",np.diag(A))
print("trace A=",np.trace(A))

conjugué
 [[ 0.03446103-0.03446103j  0.39469500-0.44742953j]
 [ 0.44742953-0.394695j    0.44164149-0.44164149j]]
transpose (attention #)
 [[ 0.03446103+0.03446103j  0.44742953+0.394695j  ]
 [ 0.39469500+0.44742953j  0.44164149+0.44164149j]]
parti imaginaire
 [[ 0.03446103  0.44742953]
 [ 0.394695    0.44164149]]
Diag A= [ 0.03446103  0.44164149]
trace A= 0.476102519896
In [42]:
import scipy.linalg as lin
A = np.array([[9,2,3], [4,9,6], [7,8,9]],dtype=float)
b = np.array([1,2,3],dtype=float)
print("det A=",lin.det(A))
x = lin.solve(A,b)
r = b - np.dot(A,x)
print("erreur =",lin.norm(r))

det A= 215.99999999999994
erreur = 4.965068306494546e-16

Problème aux valeurs propres

  • calcul valeurs propres $\lambda_n$ et vecteurs propres $u_n$ t.q. : $$A u_n = \lambda_n u_n $$
In [43]:
evals = lin.eigvals(A)
print("Valeurs propres \n",evals)
print("determinant de A=",lin.det(A))

Valeurs propres 
 [ 18.76863924+0.j   6.44597340+0.j   1.78538736+0.j]
determinant de A= 215.99999999999994
In [44]:
evals,evects = lin.eig(A)
print("vecteurs propres:\n",evects)

vecteurs propres:
 [[-0.34498864 -0.76625718 -0.17570939]
 [-0.5897528   0.58718488 -0.57005712]
 [-0.73018797  0.26089049  0.80259647]]
In [45]:
A = np.array([[4,-1,-1], [-1,4,-1], [-1,-1,4]],dtype=float)
print("vp de  A=",lin.eigvals(A))
print("norme l2=",lin.norm(A,ord=2))

vp de  A= [ 5.+0.j  2.+0.j  5.+0.j]
norme l2= 5.0

Interpolation

Interpolation polynomiale $p(x)$ de $f(x)$ passant par $n$ points $x_i$, i.e. tq $p(x_i)=f(x_i)$

    import scipy.interpolate as interp
In [46]:
import scipy.interpolate as interp
def f(x):
    return np.cos(x)
# pts d'interpolation
n=10
xp = np.linspace(0,10.0,n)
yp = f(xp)
X = np.linspace(0,10.0,100)
p1 = interp.interp1d(xp, yp)
p3 = interp.interp1d(xp, yp, kind='cubic')
In [47]:
plt.figure(figsize=(12,6))
plt.subplot(1,2,1)
plt.plot(xp,yp,'o')
plt.plot(X,f(X),'-k')
plt.plot(X,p1(X),'-',lw=2,label='lineaire')
plt.plot(X,p3(X),'-',lw=2,label='cubique')
plt.legend(loc=0)
plt.subplot(1,2,2)
plt.plot(X,p1(X)-f(X),'-',lw=2,label='lineaire')
plt.plot(X,p3(X)-f(X),'-',lw=2,label='cubique')
plt.legend(loc=0)
plt.title('Erreur')
Out[47]:
<matplotlib.text.Text at 0x7fd8530d9828>

Tracé avec Matplotlib

Matplotlib est une execellente bibliothèque Python pour du graphique 2D et 3D de données scientifiques.

  • Facile à utiliser
  • Support de $\LaTeX$
  • Contrôle de chaque élément d’une figure, y compris la taille de la figure et son DPI.
  • Sortie de haute qualité dans de nombreux formats, y compris PNG, PDF, SVG, EPS et PGF.
  • GUI et travail en mode batch

Une des caractéristiques de Matplotlib est le contrôle complet de la figure par le programmeur. C’est un point important pour la reproductibilité des résultats lorsque l’on a besoin de régénérer la figure avec des données mises à jour.

Plus d’informations sur la page Web Matplotlib: http://matplotlib.org/

Utilisation sous Python

    import matplotlib.pyplot as plt
In [48]:
# donnees
F = lambda x: np.sin(x)/x
x = np.linspace(1.e-10, 10, 100)
y = F(x)
# tracer
fig = plt.figure(figsize=(8,8))
axes1 = fig.add_axes([0.1, 0.1, 0.8, 0.8]) # main axes
axes2 = fig.add_axes([0.4, 0.5, 0.4, 0.3]) # inset axes
# main figure
axes1.plot(x, y,'--b',lw=2)
axes1.set_xlabel('x')
axes1.set_ylabel('y')
axes1.axhline(y=0,c='k')
axes1.set_title('fonction $y=f(x)$')
# insert
axes2.plot(y, x, 'g',lw=2)
axes2.set_xlabel('$y=\\frac{sin(x)}{x}$')
axes2.set_ylabel('x')
axes2.set_title('fonction inverse $y=f^{-1}(x)$');

Exemples sur le site de matplotlib

In [49]:
from IPython.display import HTML
HTML('<iframe src=http://matplotlib.org/gallery.html width=700 height=350></iframe>')
Out[49]:

Documentations supplémentaires

Version de Python et des bibliothéques

In [50]:
print("\t\tSystème utilisé")
import sys
print("Système :\t\t",sys.platform)
import platform
print(platform.platform())
print("Ordinateur:\t\t",platform.machine())
print("Version de Python:\t",sys.version)
import IPython
print("Version de IPython:\t",IPython.__version__)
import numpy
print("Version de numpy:\t",numpy.version.version)
import scipy
print("Version de scipy:\t",scipy.version.version)
import matplotlib
print("Version de matplotlib:\t",matplotlib.__version__)

		Système utilisé
Système :		 linux
Linux-4.4.0-112-generic-x86_64-with-Ubuntu-16.04-xenial
Ordinateur:		 x86_64
Version de Python:	 3.5.2 (default, Nov 23 2017, 16:37:01) 
[GCC 5.4.0 20160609]
Version de IPython:	 6.2.1
Version de numpy:	 1.11.0
Version de scipy:	 1.0.0
Version de matplotlib:	 1.5.1

Fin de la leçon