- mer. 31 janvier 2018
- Cours
- #ipython jupyter
Table des matières
- 1 Calcul scientifique avec Python
- 2 Fonctionnement d’un ordinateur
- 3 Historique des langages
- 4 Exigences du calcul scientifique
- 5 Algorithme
- 6 Langage Python
- 7 Base de programmation sous Python
- 8 Fin
%matplotlib inline
import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
from matplotlib import rcParams
rcParams['font.family'] = 'serif'
rcParams['font.size'] = 14
# option de mise en page
from IPython.core.display import HTML,display
css_file = 'style.css'
HTML(open(css_file, "r").read())
# edit metadata "livereveal": {"scroll": true }
# https://damianavila.github.io/RISE/customize.html"
Calcul scientifique avec Python¶
Marc BUFFAT, dpt mécanique, Université Lyon 1
(**) voir le cours “Scientific Python Lectures” by Robert Johansson

Mise à disposition selon les termes de la Licence Creative Commons
Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 2.0 France.
Objectifs¶
Apprendre:¶
- concept fondamentaux en programmation
- différentes techniques de base
- démarche de programmation scientifique
- syntaxe du langage Python
À la fin du cours, vous pourrez:¶
- résoudre des problèmes scientifiques (à l’aide de Python)
- appliquer la démarche de programmation scientifique avec d’autres langages (matlab, scilab, ..)
Fonctionnement d’un ordinateur¶
ordinateur = matériel (CPU, mémoire, disque,..) + logiciel (OS, programmes,..)
composants¶
OS
Système d’exploitation (OS) = gestion d’un ordinateur + environement
Linux/Unix = vue abstraite et générique indépendante du matériel
programmes + données
- programme = processus
- données = fichiers (files, devices, streams)
- gestion des droits: notion d’utilisateur (user), groupes (group), autres (other)
- super-utilisateur: root
Principes
small is beautiful
generality is better than specificity
communication is important (format ouvert pour les données)
programmes / processus¶
processus = programme executé sur un ordinateur
- pid = numéro du processus
- programme (utilisateur ou commande système)
- E/S: entrée par défaut (input stream=stdin), sortie par défaut (output stream=stdout)
- sortie programme = entrée d’un autre programme : pipe ou |
- pge 1 | pge 2 | pge 3
- controle des processus: kill pid ou ctrl+C, stop (ctrl+Z) , tache de fond (bg) , ps, top
- éxecution des commandes à travers une interface
- un terminal avec un shell (interpérteur de commande): bash (avec auto-complétion)
- un GUI (gnome, KDE, ..)
syntaxe (attention majuscule # minuscule, espace = séparateur d’arguemnts)
cde [-options] arguments
%%bash
ps -au buffat | head
Système de fichiers (Unix)¶
vu arborescente abstraite indépendante du matériel à partir de la racine (root) /
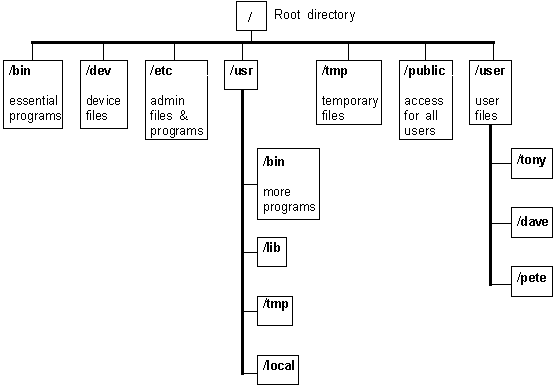
notation
- fichier = nom de fichier + répertoire + droits d’accés
- / séparateur de répertoire (directory)
- . répértoire courant
- .. répértoire parent
- pwd : affiche répertoire courant
- lien symbolique
- fichiers cachés: commence par .
principales commandes
- ls : liste des fichiers
- mkdir : création répertoire
- rm : éfface un fichier
- cd : change de répertoire (directory)
- help cde : aide
- cat file : affiche le contenu du fichier
%%bash
ls -al | head
Algorithme de base¶
Algorithme Serie(x,n)
somme = 0
pour i de 1 a n
somme=somme + (-1)^(i+1)*x^i/i
retour sommeEcrire un algorithme plus efficace en notant que:
$$ (-1)^{i+1} \frac{x^i}{i} = - \frac{x}{i} (-1)^{i} x^{i-1} $$Execution sur un ordinateur¶
L’ordinateur (le CPU) n’éxécute que des instructions machines codées en binaire.
Problème: comment transformer un algorithme en langage machine ?
Langage machine (binaire)¶
- suite d’instruction binaire executer par le processeur: 01010111 (suite 0 ou 1 : bits)
- représentation en hexadécimal (octet ou bytes):
- f8 = 248
- instructions et données sont stockées en mémoire (à une adresse donnée)
- @000141 instruction f8
- spécifiques au processeur (intel, ARM, power, AMD, ..)
- spécifique au système d’exploitation OS
%%bash
od -x -N 100 data/a.out
./data/a.out
Langage assembleur¶
L’assembleur traduit le code source en code binaire
- notation des instructions machines (move, push, load, add, mul)
- programme + assembleur = code machine
%%bash
head -15 data/serie.s
Langage compilé: compilateur¶
le compilateur transforme le code source en assembleur (compilation), éffectue l’édition avec des librairies pour obtenir un binaire qui dépend de l’ordinateur cible, mais qui s’exécute sans le compilateur et sans le code source.
- C++ Fortran C
- programme source + compilateur = programme binaire
- programme source = portable
- programme binaire = spécifique à l’ordinateur (non portable)
 langage C
langage C
%%bash
head -17 data/serie.C
%%bash
g++ data/serie.C -o serie
./serie
Langage interprété:¶
l’interpéteur exécute de façon interactive chaque ligne du fichier pour la traduire en code machine et l’execute interactivement. Pour exécuter le code, on a donc toujours besoin de l’interpréteur et du code source.
- Python, Matlab
- programme + interpréteur
- portable = indépendant du système (Linux, MacOS, Windows)
langage python
Python est un language de programmation moderne de haut niveau, logiciel libre, généraliste, multi-plateformes, multi-architecture, multi-OS (linux, windows, MacOS,..). Un programme python peut s’executer sur un tout petit raspberry Pi à 30€ (ARM), sur des smartphones, des portables, des PC jusqu’aux super-calculateurs HPC avec $10^9$ coeurs de calcul.
%%bash
cat data/serie.py
%%bash
python data/serie.py
Historique des langages¶
Langages de programmation¶
Années 1950 (approches expérimentales) :
- FORTRAN, LISP, COBOL…
Années 1960 (langages universels) :
- ALGOL, PL/1, PASCAL…
Années 1970 (génie logiciel) :
- C, MODULA-2, ADA…
Années 1980 (programmation objet) :
- C++, Eiffel…
Années 1980 (boites à outils):
- LabView, Matlab…
Années 1990 (langages interprétés objet) :
- Java, Perl, Python…
Langages pour les scientifiques¶
Pour le calcul intensif (HPC) (Argonne Lab)
- C,C++
- Fortran
- Python
Matlab est très utilisé pour le traitement des données, mais peut être avantageusement remplacer par Python avec ses librairies numpy et matplotlib et pandas
Exigences du calcul scientifique¶
“Le logiciel (software) est une des pierres angulaires de la science moderne. Sans logiciel, la science du vingt et unième siècle serait impossible. Mais sans de meilleurs logiciels, la science ne peut pas progresser” [http://sciencecodemanifesto.org/]
Réplicabilité et de reproductibilité sont des pierres angulaires de la méthode scientifique. En ce qui concerne le travail numérique, se conformer à ces concepts a des implications pratiques suivantes:
Réplicable: L’auteur d’un article scientifique qui implique des calculs numériques doit être en mesure de relancer les simulations et de reproduire les résultats sur demande. D’autres scientifiques devraient également être en mesure d’effectuer les mêmes calculs et d’obtenir les mêmes résultats, compte tenu des informations sur les méthodes utilisées dans une publication.
Reproductible: Les résultats obtenus à partir de simulations numériques doivent être reproductibles avec une mise en oeuvre indépendante du procédé, ou en utilisant un procédé tout à fait différent.
En résumé: un résultat scientifique solide doit être reproductible, et une étude scientifique solide doit être réplicable.
importance de la documentation
importance de la validation
importance de la maîtrise du code et des transformations de données (logiciels libres)
</ol>
Démarche du calcul scientifique¶
- Modèle mathématique
- Discrétisation numérique: solution approchée
- Recherche solution algorithmique
- Programmation
- Validation
Algorithme¶
algorithme = suite finie et non ambigüe d’opérations ou d’instructions sur des données permettant d’obtenir un résultat (numérique) pour résoudre un problème
Dans un algorithme numérique
- identifier les données
- identifier le résultat
- identifier les transformations des données pour obtenir le résultat
définir des cas de validation
l’algorithme est ensuite traduit dans un langage de programmation sous forme de fonction (ou procédure)
Attention fonction algorithmique $\neq$ fonction mathématique
Exemple: calcul d’une série¶
Formulation mathématique: calcul de la somme d’une série¶
$$ S_N = x - \frac{x^2}{2} + \frac{x^3}{3} + .. = \sum_{i=1}^n (-1)^{i+1} x^i/i $$Solutions algorithmiques¶
1ere solution
Algorithme Serie(x,n)
somme = 0
pour i de 1 a n
somme=somme + (-1)^(i+1)*x^i/i
retour somme
2nde solution (optimisée)
Algorithme Serie(x,n)
somme = 0
coeff = x
pour i de 1 a n
somme = somme + coef/i
coef = -coef*x
retour sommeimplémentation¶
# algorithme en Python
from numpy import log
def serie(x,n):
""" calcul de la somme de n termes de la serie x-x^2/2+x^3/3- """
coef=x
somme=0.0
for i in range(1,n+1):
somme = somme + coef/i
coef = -coef*x
return somme
Test et Validation¶
$$ \lim_{N\rightarrow\infty} S_N = log(1+x) $$# utilisation et validation
x=0.2
n=10
print("Calcul de la serie pour x=",x," et n=",n)
print("somme = ",serie(x,n))
print("log(1+x) = ", log(1+x))
err = serie(x,n) - log(1+x)
print("erreur: ",err)
Cours en ligne sur Python¶
Introduction au calcul scientifique avec Python¶
http://ufrmeca.univ-lyon1.fr/~buffat/COURS/INPROS.html
- COURS InProS ”Introduction à la Programmation Scientifique”
Caractéristiques de Python¶
Python (http://www.python.org/) est un langage de programmation moderne de haut niveau, orienté objet et d’usage général.
Caractéristiques générales de Python:
- Langage simple: facile à lire et à apprendre avec une syntaxe minimaliste.
- Langage concis et expressif: moins de lignes de code, moins de bugs, plus facile à maintenir.
Détails techniques:
- Typé dynamiquement: Pas besoin de définir le type des variables, les arguments ou le type des fonctions.
- La gestion automatique de la mémoire: Aucune nécessité d’allouer explicitement et désallouer la mémoire pour les variables et les tableaux de données. Aucun bug de fuite de mémoire.
- Interprété: Pas besoin de compiler le code. L’interpréteur Python lit et exécute le code python directement.
Avantages:¶
- Le principal avantage est la facilité de programmation, qui minimise le temps nécessaire pour développer, déboguer et maintenir le code.
- Langage bien conçu qui encouragent les bonnes pratiques de programmation:
- Modulaire et orientée objet, permet l’encapsulation et la réutilisation de code. Il en résulte souvent un code plus transparent, maintenable et sans bug.
- Documentation intégré avec le code.
- De nombreuses bibliothèques standards, et de nombreux packages add-on.
Inconvénient:¶
- peut etre (très) lent, mais c’est le propre des langages interprétés
- manque de certaines boites à outils (simulink,…)
Les bonnes pratiques de la programmation¶
import this
%%bash
python <<EOF
print 1+2./537
EOF
programmation (avec un éditeur)¶
%%bash
cat data/serie.py
%%bash
python data/serie.py
Ipython Notebook¶
IPython notebook est un environnement portable sous HTML pour Python, similaire à Mathematica ou maple. Il est basé sur un shell IPython, mais offre un environnement à base de cellules avec une grande interactivité, où les calculs peuvent être organisées documentée de manière structurée.
Par defaut les cellules executent du code Python en cliquant sur le bouton “run” ou en entrant ctrl+entrée; avec le menu Cell->Run All on execute toutes les cellules dans l’ordre. On peut aussi éffacer toute les sorties avec All output -> Clear
print("hello ceci est mon premier programme")
On peut aussi ajouter du texte en changeant le type de cellule de code a markdown
On peut alors utiliser des balises de mise en page markdown (documentation sur le lien ci-dessous)
exemples
# titre niveau 1
## titre niveau 2
### titre niveau 3
**texte** écriture texte en gras
$ formule $ affichage formule en LaTeX
$$ equation $$ ou une équation
remarque en double cliquant sur une cellule, on peut modifier cette cellule
De nombreux exemples de notebook sont accesibles [http://nbviewer.jupyter.org/] ou sur le site [http://jupyter.org/]
HTML('<iframe src="http://nbviewer.jupyter.org/" height=400 width=800/>')



