Marc BUFFAT

Marc BUFFAT

Professeur au département de Mécanique, Lyon 1 e-mail

Blog scientifique et pédagogique utilisant des notebooks IPython et Linux

Cours Python scientifique

Table des matières

In [1]:
%matplotlib inline
#%autosave 300
import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
from matplotlib import rcParams
rcParams['font.family'] = 'serif'
rcParams['font.size'] = 14
from IPython.core.display import HTML
from IPython.display import display
from matplotlib import animation
css_file = 'style.css'
HTML(open(css_file, "r").read())
# edit metadata   "livereveal": {"scroll": true }
# https://damianavila.github.io/RISE/customize.html"
Out[1]:

Base de la programmation

Marc BUFFAT, dpt mécanique, Université Claude Bernard Lyon 1

Rappel de programmation Python

Python tutor: http://pythontutor.com

Outil en ligne permettant de visualiser l’execution d’un programme Python

Variable

variable:

  • case mémoire pour stocker de l’information
  • doit être déclaré (initialisé) avant d’être utilisé
In [2]:
x=1
x=x+1
y=2*x+1
x=y+1

Type de variable

fonction du type de l’information (entier, réel, chaine)

In [3]:
x=1
print(type(x))
x=1.0
print(type(x))
x='1'
print(type(x))

<class 'int'>
<class 'float'>
<class 'str'>

Initialisation d’une variable

attention on doit définir une variable (sa valeur) avant de l’utiliser !!

In [4]:
# erreur !
Y=X

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
<ipython-input-4-231a1f6bb380> in <module>()
      1 # erreur !
----> 2 Y=X

NameError: name 'X' is not defined
In [5]:
# modification:  X,Y,x sont 3 variables #
Y=x
X=2
print(X,Y,x)
x=3
print(X,Y,x)

2 1 1
2 1 3

Portée d’une variable

Attention: dans une fonction les arguments et les variables dans la fonction sont locales.

Quelles sont les valeurs des variables a,b,c après execution du programme ci-dessous ?

In [8]:
a=3
c=-3
def func1(a,b):
    c=0
    def func2(a,b):
        c = a - b
        return c
    c=func2(b,a)
    return c
a=func1(2,1)

execution du code avec pythontutor

In [9]:
%load_ext tutormagic
In [10]:
%%tutor --lang python3 -h 400
a=3
c=-3
def func1(a,b):
    c=0
    def func2(a,b):
        c = a - b
        return c
    c=func2(b,a)
    return c
a=func1(2,1)

argument d’une fonction

Lors de l’appel d’une fonction, les arguments peuvent être des expressions, des valeurs ou des variables (si elles sont initialisées)

In [11]:
# exemple d'arguments
func1(x,x+1)
func1(c,2)
a=func1(a,a)

liste et tableau

  • liste: ensemble ordonné de valeurs

    • ajout et suppression d’éléments
    • la taille et le type peuvent variés

  • tableau: ensemble ordonné de valeurs de même type

    • vecteurs, matrices
    • taille fixée

  • indice: on compte à partir de 0

    • indice à partir de 0
    • [ ] pour sélectionner un élèment
    • [0] premier element
    • [-1] dernier element
    • [n0:n1:p] selection des elements de l’indice n0 (defaut 0) à n1 (exclus) avec un pas p (defaut 1)
    • aliasing attention à la copie
      • A=B aliasing (A et B sont identiques)
      • A=B[:] copie
In [12]:
#  manipulation de liste
L=[1,2,3]
L1=L[:]
L1[-1]=4
L[0]=5
print(L,L1)

[5, 2, 3] [1, 2, 4]

execution du code avec pythontutor

In [13]:
%%tutor --lang python3
L=[1,2,3]
L1=L[:]
L1[-1]=4
L[0]=5
In [14]:
# manipulation de tableau (avec aliasing)
X=np.linspace(1,5,5)
Y=X
Z=2*X
Y[0]=0
X[0]=Y[1]
Z[0]=1
print(X,Y,Z)

[ 2.  2.  3.  4.  5.] [ 2.  2.  3.  4.  5.] [  1.   4.   6.   8.  10.]

Erreur algorithmique

exemple 1

Pour éffectuer une permutation circulaire à droite d’un tableau X : $X_{i+1}=X_i$ (décalage à droite), on utilise l’un des deux programmes suivants. L’un est algorithmiquement faux. Lequel ?

In [15]:
# decalage a droite: version 1
n = 5
X = np.linspace(1,5,5)
a = X[-1]
for i in range(n-1):
    X[i+1]=X[i]
X[0]=a
In [16]:
# decalage a droite: version 2
n=5
Y=np.linspace(1,n,n)
x=Y[-1]
for i in range(1,n):
    Y[n-i]=Y[n-i-1]
Y[0]=x
In [17]:
# validation
print(X)
print(Y)

[ 5.  1.  1.  1.  1.]
[ 5.  1.  2.  3.  4.]

exemple 2

Calcul de l’expression

  pour i de a N
$$ Y_i = Y_i - \frac{\sum_{j=1}^{N} A_{ij} Y_j - B_i}{A_{ii}} $$

  fin i

Pour calculer cette expression, on utilise l’une des deux fonctions suivantes. L’une est algorithmiquement fausse. Laquelle ?

In [18]:
# version 1
def iteration1(A,B,X):
    n = X.shape[0]
    Y = X[:]
    for i in range(n):
        sum=0.0
        for j in range(n):
            sum = sum + A[i,j]*Y[j]
            Y[i] = Y[i] - (sum - B[i])/A[i,i]
    return Y
In [19]:
# version 2
def iteration2(A,B,X):
    n = X.shape[0]
    Y = X[:]
    for i in range(n):
        sum=0.0
        for j in range(n):
            sum = sum + A[i,j]*Y[j]
        Y[i] = Y[i] - (sum - B[i])/A[i,i]
    return Y
In [20]:
# exemple de validation
n=3
X=np.random.rand(n)
A=np.random.rand(n,n)
B=np.random.rand(n)
# 
X1=iteration1(A,B,X)
print("X1=",X1)
X2=iteration2(A,B,X)
print("X2=",X2)

X1= [ 3.38348358  0.10726331 -1.44650396]
X2= [ 8.47078332  0.08940713 -6.09000326]

programmation récursive

  • la fonction s’appelle elle-même
  • calcul factorielle n!
    • n! = n*(n-1)!

Que calcule la fonction récursive suivante ?

In [21]:
def fonc(L):
    print("appel fonc avec ",L)
    if not L:
        return 0
    else:
        return 1 + fonc(L[1:])
In [22]:
# resultat
fonc([1,2,3,4])

appel fonc avec  [1, 2, 3, 4]
appel fonc avec  [2, 3, 4]
appel fonc avec  [3, 4]
appel fonc avec  [4]
appel fonc avec  []
Out[22]:
4

Erreur sous Python

retour erreur

   Traceback (most recent call last):
    File "test.py", line 6, in <module>
    test()
    File "test.py", line 3, in test
    print table[4]
    IndexError: list index out of range

code d’erreurs

  • IndentationError :

      expected an indented block

  • IndexError:

      list index out of range

  • SyntaxError :

      inconsistent use of tabs and spaces in indentation

  • NameError :

      name 'X' is not defined

  • ImportError :

      no module named X

  • ZeroDivisionError :

      X division or modulo by zero

Python 3

  • print est une fonction

    print("Bonjour")

au lieu de (python 2.7)

  print "Bonjour"

  • la division / est une division réelle (entière sous python 2.7)

    4 / 2 = 2.0

4 // 2 = 2
In [23]:
# fonction de formattage 
print("Bonjour {} {}".format("Marc","Buffat"))

Bonjour Marc Buffat
In [24]:
# division entière et réelle
print("division : ",4/2, 4//2)
print("division : ",1/2, 1//2)

division :  2.0 2
division :  0.5 0

Programmation sctructuré

principe: “Divide and Conquer”

analyse descendante: top-down design

  • définition des différentes étapes pour résoudre le problème
  • on découpe le problème en une série de sous-problèmes plus simples (si possible indépendant)
  • on spécifie ce qui doit résolu dans chacun des sous-problèmes sans forcément dire comment
  • puis on itère au niveau des sous problèmes.

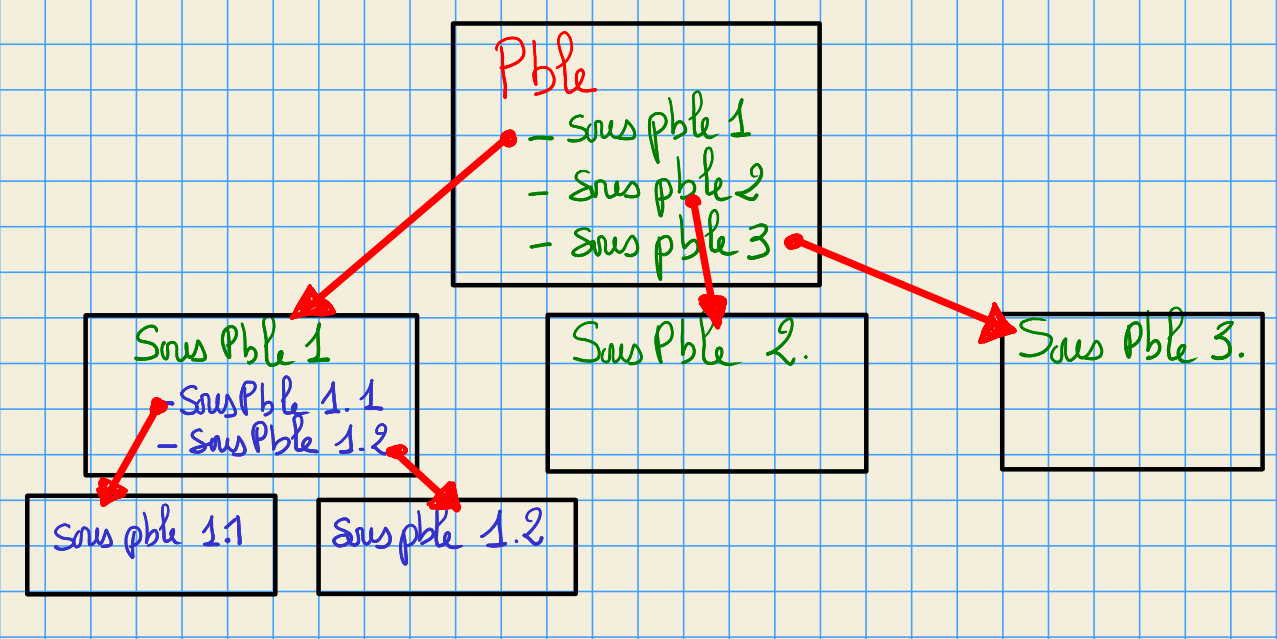
analyse top-down

programmation ascendante: bottom-up programming

  • on programme d’abord les sous-problèmes(sous forme de fonction)
  • on validation les fonctions
  • puis on réitère en remontant dans l’arbre jusqu’au programme principal
  • on crée une bibliothéque

  • on éffectue l’analyse et la validation globale

    règles réutiliser les fonctions déjà écrites et validées (bibliothèques): principe du moindre effort !

Exemple: simulation de l’alunissage de Neil Amstrong (Apollo 11)

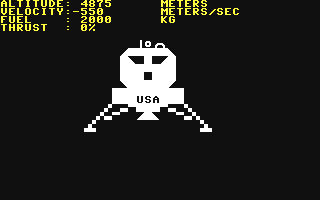
Moon lander

On a perdu le pilotage automatique et il faut oser le module lunaire (LEM) sur la lune en arrivant avec une vitesse quasiment nulle. Pour cela on dispose de rétro-fusées permettant de ralentir la chute du LEM.

  • On contrôle manuellement ces rétro-fusées en sélectionnant une poussée (de 0 à 9), correspondant à l’éjection de carburant avec un débit $Qe$ variable et une vitesse $Ue$ fixe.
  • Mais on dispose d’une quantité limitée de carburant que l’on doit utiliser avec modération pour pouvoir atterrir en douceur.

modèle physique

Le LEM, de masse initiale $M0$, est soumis à la gravité $g$ de la lune et à la poussée des rétro-fusées, correspondant à l’éjection d’un débit de fuel $Qe$ à un vitesse $Ve$ . LEM

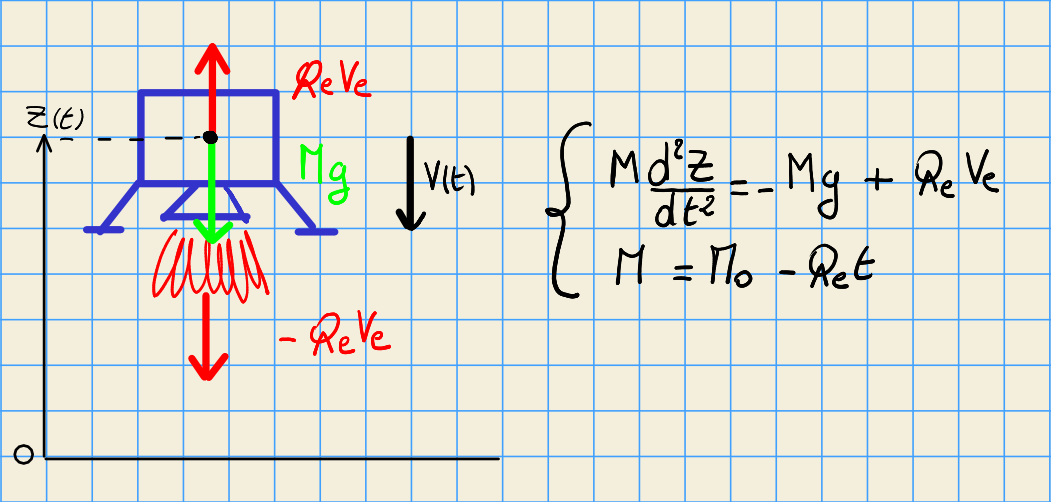
modèle mathématique

Equation du mouvement: $$ \frac{d^2 Z}{dt^2} = -g + \frac{Qe*Ue}{M0-Qe*t}$$

en intégrant sur la durée d’une commande $T$ $\rightarrow$ vitesse $V$ $$ V = V0 + g*T + Ue * \ln{(1 - \frac{Qe*T}{M0})} $$ La masse du LEM $M$ diminue $$M = M0 -Qe*T$$ Approximation par DL car $X=\frac{Qe*T}{M0} \ll 1$ $$ V = V0 + g*T - Ue*(X + \frac{X^2}{2} + \frac{X^3}{3} + \frac{X^4}{4} + \frac{X^5}{5})$$ d’où l’altitude $Z$ $$ Z = Z0 - V0*T - g \frac{T^2}{2} + Ue*T*(\frac{X}{2} + \frac{X^2}{6} + \frac{X^3}{12} + \frac{X^4}{20} + \frac{X^5}{30})$$ expression utilisée dans les premiers programmes en BASIC.

cas particuliers

  1. Si le fuel est épuisé ($Qe=0$), le LEM atteins la surface lunaire au bout d’un temps $T$ solution de l’équation du 2nd degré: $$ 0 = Z0 - V0*T -g \frac{T^2}{2}$$ soit $T = (-V0 + \sqrt{V0^2 + 2 g Z0})/g$

  2. Près de la surface, $T$ trop grand $\rightarrow$ prédiction $Z0 < 0$

    • calcul $T$ donnant l’altitude $Z=0$, solution d’une équation du 6ième degré.
    • calcul par approximations successives en utilisant un DL de $Z(t)$
      1. estimation $T0$ de $T$ $$ T0 = \frac{-V0 + \sqrt{V0^2 + 2 (g-\frac{Ue*Qe}{M0}) Z0}}{g-\frac{Ue*Qe}{M0}} $$
      2. recalcule $V0$ et $Z0$, puis recommence.

Algorithme: analyse top-down

problème global

problème global

sous-problème lecture commande

problème global

sous-problème VitesseAltitude

applications des formules mathématiques de l’analyse précédente

$$ V = V0 + g*T - Ue*(X + \frac{X^2}{2} + \frac{X^3}{3} + \frac{X^4}{4} + \frac{X^5}{5})$$$$ Z = Z0 - V0*T - g \frac{T^2}{2} + Ue*T*(\frac{X}{2} + \frac{X^2}{6} + \frac{X^3}{12} + \frac{X^4}{20} + \frac{X^5}{30})$$

sous-problème Alunissage

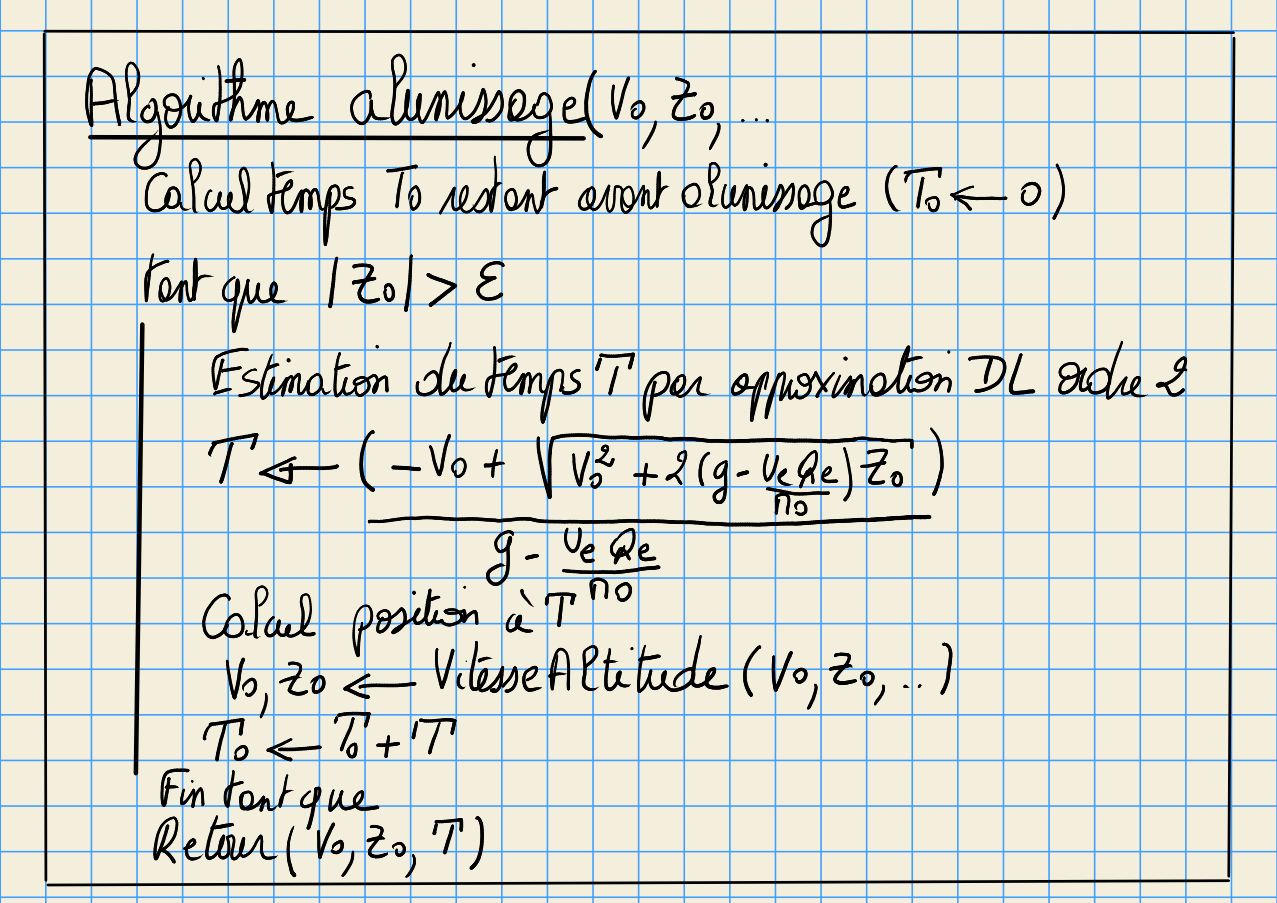
problème global

Implémentation fonctions python

In [25]:
%%bash
cat alunissage.py

#! /usr/bin/env python3
# -*- coding: utf-8 -*-
""" programme de simulation d'alunnissage
    basée sur le programme BASIC LUNAR 
    de Jim Storer sur PDP-8 en 1969 """

import numpy as np
# constantes en unité SI (kg/m/s)
g  = 1.6     # gravité
Ue = 2900.   # vitesse d'ejection
#
def Lecture_Cde(V0,Z0,Me,dt,ch):
    ''' renvoie la poussee Qe et son temps d'application T
        compte tenu de la vitesse V0, position Z0, 
        masse de fuel restante Me 
        du pas de temps dt et d'une commande ch (0-9) '''
    global g
    T=dt
    if Me>0 :
        # calcul poussée
        if (ch>='1') and (ch<='9') :
                Qe = int(ch)*10 # pousse en kg/s
        else:
                Qe = 0
        # test si reserve de fuel suffisante
        if (Me-Qe*T)<0 :
            # temps restant d'utilisation du fuel
            T = Me/Qe
    else:
        print("Plus de fuel ")
        Qe = 0
        # calcul du temps T pour parcourir Z0 (alunissage)
        T = (-V0 + np.sqrt(V0*V0 + 2*g*Z0)) / g
    return Qe,T

def VitesseAltitude(V0,Z0,X,T):
    """ calcul de la nvlle vitesse en fonction de la vitesse V0
        un débit sans dimension X=Qe*T/M0 de fuel, pendant  T
        ainsi que de la nouvelle altitude du LEM
    """
    global g,Ue
    V = V0 + g*T - Ue*(X + X*X/2. + X**3/3. + X**4/4. + X**5/5.)
    Z = Z0 - V0*T - g*T*T/2. + Ue*T*(X/2. + X*X/6. + X**3/12. + X**4/20. + X**5/30.)
    return V,Z

def Alunissage(V0,Z0,M0,Qe):
    """ calcul etat a Z=0 a partir d'une CI V0,Z0,M0 et Qe
       calcul du temps T0 pour alunissage 
       par approximation successive
       retour etat V0,Z0,T0 """
    global g,Ue
    T0 = 0
    while np.abs(Z0) > 1.e-2:
            T= (-V0 + np.sqrt(V0*V0 + 2*(g-Ue*Qe/M0)*Z0)) / (g-Ue*Qe/M0)
            V0,Z0 = VitesseAltitude(V0,Z0,Qe*T/M0,T)
            T0 = T0+ T
    return V0,Z0,T0

programme principale

In [26]:
from alunissage import Lecture_Cde, VitesseAltitude, Alunissage
# conditions initiales
#Z0 = 190000. # position
Z0 = 100000
V0 = 1580.   # et vitesse
M0 = 15000.  # masse initiale du LEM
Me = 8000.   # dont une masse de fuel
t  = 0.      # temps simulation
dt = 10.     # pas en temps entre chaque commande
# sauvegarde données
alt=[Z0]
vit=[V0]
tps=[0.]
fuel=[Me]
print("Simulation alunissage")
while np.abs(Z0)>1.e-2 :
    ch = input("commande (0-9):")
    Qe,T = Lecture_Cde(V0,Z0,Me,dt,ch)
    # calcul de la nouvelle position du LEM
    V1,Z1 = VitesseAltitude(V0,Z0,Qe*T/M0,T)
    # test si alunnissage
    if Z1 < 1.e-2 :
        V1,Z1,T = Alunissage(V0,Z0,M0,Qe)
    # mise a jour de la position du LEM
    Z0 = Z1;      V0 = V1
    Me = Me-Qe*T; M0 = M0-Qe*T
    t  = t + T
    print("t=",int(t),"s Z=",int(Z0),"m V=",int(V0),"m/s fuel=",int(Me),"kg")
    # sauvegarde donnérs
    alt.append(Z0)
    vit.append(V0)
    tps.append(t)
    fuel.append(Me)
# fin simulation
print("Alunissage avec une vitesse ",int(V0)," m/s")
if V0<=0.5 :
    print("Alunissage parfait")
elif V0<=5. :
    print("Bon alunissage, mais perfectible")
elif V0<=27.:
    print("Accident à l'alunissage. Attendez les secours en esperant que vous avez assez d'oxygene !!!")
else :
    print("Crash fatal: aucun survivant")

Simulation alunissage
commande (0-9):9
t= 10 s Z= 85007 m V= 1416 m/s fuel= 7100 kg
commande (0-9):8
t= 20 s Z= 71601 m V= 1263 m/s fuel= 6300 kg
commande (0-9):6
t= 30 s Z= 59553 m V= 1145 m/s fuel= 5700 kg
commande (0-9):4
t= 40 s Z= 48482 m V= 1068 m/s fuel= 5300 kg
commande (0-9):7
t= 50 s Z= 38558 m V= 914 m/s fuel= 4600 kg
commande (0-9):8
t= 60 s Z= 30356 m V= 723 m/s fuel= 3800 kg
commande (0-9):3
t= 70 s Z= 23449 m V= 657 m/s fuel= 3500 kg
commande (0-9):2
t= 80 s Z= 17071 m V= 617 m/s fuel= 3300 kg
commande (0-9):9
t= 90 s Z= 12118 m V= 368 m/s fuel= 2400 kg
commande (0-9):8
t= 100 s Z= 9621 m V= 126 m/s fuel= 1600 kg
commande (0-9):5
t= 110 s Z= 9133 m V= -30 m/s fuel= 1100 kg
commande (0-9):8
t= 120 s Z= 10845 m V= -316 m/s fuel= 300 kg
commande (0-9):7
t= 124 s Z= 12445 m V= -431 m/s fuel= 0 kg
commande (0-9):4
Plus de fuel 
t= 690 s Z= 0 m V= 475 m/s fuel= 0 kg
Alunissage avec une vitesse  475  m/s
Crash fatal: aucun survivant
In [27]:
plt.figure(figsize=(16,8))
plt.subplot(1,3,1)
plt.plot(tps,alt,lw=2)
plt.title("altitude")
plt.subplot(1,3,2)
plt.plot(tps,vit,lw=2)
plt.title("vitesse")
plt.subplot(1,3,3)
plt.plot(tps,fuel,lw=2)
plt.title("fuel")
Out[27]:
<matplotlib.text.Text at 0x7fc73c657f28>

version avec ncurses

python lunar_landing.py

FIN

In [ ]: