M2 images

TP5 - TAA / Temporal Anti Aliasing

Le TAA est utilisé dans quasi-tous les codes de rendu temps réel... Le principe est simple : au lieu de tout calculer à chaque image, TAA va permettre de ne calculer qu'une partie des résultats et d'accumuler ces résultats partiels avec les résultats précédents.
Par exemple, au lieu de calculer l'influence de 256 sources de lumières sur chaque fragment, il devient possible de n'évaluer que quelques sources à chaque image. Par exemple 32 sources par image... Par contre, il faudra 8 images pour accumuler la totalité des 256 sources. On vient d'introduire de la latence dans le calcul de l'éclairage, mais on vient aussi de gagner beaucoup de temps sur le calcul de l'image complète. Pourquoi vouloir faire ça ? Peut-être parce que cette modification permet de rendre 60 ou 120 images par secondes et de rester parfaitement fluide, sans aucune saccade dans l'affichage. A 60 images par seconde, 8 images ne représentent que 128ms ou 0.1s...

On peut bien sur utiliser TAA pour anti-aliasser l'image complète ! en remplacant les n points testés par la fragmentation / rasterization des triangles par un seul, ce qui est encore plus appréciable lorsque le code de rendu utilise le rendu différé. on peut aussi l'utiliser pour filtrer les textures opaques et même les textures semi-transparentes !

alors c'est magique ? sur une image fixe ? oui, sur une image en mouvement, beaucoup moins...

Partie 1 : comment ça marche ?

Sur une image fixe, le principe est très simple. on suppose que l'on a décomposé nos calculs en N étapes :

pour l'image i sur N,
réaliser la ième étape de calculs intermédiaires pour chaque pixel de l'image,
accumuler chaque pixel avec les résultats des étapes précédentes, de 0 à i-1,
afficher l'accumulation.

Il est assez direct de n'utiliser qu'une seule image "historique" qui permet d'accumuler les images précédentes, au lieu de stocker séparément chaque image intermédiaire et d'accumuler répétitivement les étapes précédentes.

historique= 0
pour l'image i sur N,
réaliser la ième étape de calculs intermédiaires pour chaque pixel de l'image,
historique= historique + image,
afficher historique.

Parfait ! et si on veut calculer une moyenne sur N valeurs, qu'est ce qui change ? on peut simplement diviser par N au moment de l'affichage, on peut aussi calculer incrémentalement la moyenne, ie l'historique contient la moyenne des étapes 0 à i-1 inclus, et on pondère le nouveau résultat pour calculer la moyenne des étapes 0 à i inclus.

comment ?
on note \( \bar{x}_n \) la moyenne des n premières étapes, ie de 0 à i-1.
\[
    \bar{x}_{n}= \frac{1}{n} \sum_{i=0}^{n-1} x_i
\]

on ajoute \( x_i \) le résultat de la ième étape pour obtenir \( \bar{x}_{n+1} \) la moyenne des n+1 premières étapes.
\[
    \bar{x}_{n+1}= \frac{1}{n+1} (n \cdot \bar{x}_{n} + x_i)
\]

ou sous une forme plus lisible :
\[
    \bar{x}_{n+1}= \frac{n}{n+1} \bar{x}_{n} + \frac{1}{n+1} x_i
\]
encore plus simple, en se rappelant que l'on peut ré-écrire \( \frac{n}{n+1} \) comme \( \frac{n+1}{n+1} - \frac{1}{n+1} \)
\[
    \bar{x}_{n+1}= \left(1 - \frac{1}{n+1} \right) \bar{x}_{n} + \frac{1}{n+1} x_i
\]

et on peut ré-ecrire la boucle d'accumulation sous la forme utilisée dans les articles qui décrivent TAA :

historique= 0
pour l'image i sur N,
    réaliser la ième étape de calculs intermédiaires pour chaque pixel de l'image,
    // historique est la moyenne de i valeurs...
    historique= (1 - 1 / (i+1)) historique + 1 / (i+1) image,
afficher historique.

Et dans le cas normal, sur une image en mouvement ?
Il va falloir trouver sur quel pixel accumuler chaque étape. Dans le cas "fixe", les résultats du pixel (x,y) sont accumulés sur le même pixel de l'image qui contient l'historique, ie l'accumulation des étapes précédentes. Si la camera ou les objets bougent, il va falloir reprojeter le fragment visible pour le pixel (x,y) dans l'image précédente. Il suffit de garder les transformations utilisées pour dessiner les objets lors de l'image précédente et de modifier le vertex shader pour calculer les 2 transformations : celle de l'image i qui est en cours de dessin / calcul ainsi que la transformation utilisée pour l'image précédente, i-1. Il reste un tout petit problème à régler : on est pas du tout sur que le point du triangle visible sur le pixel (x,y) à l'image i est le même que le point visible sur le pixel reprojetté à l'image i-1 !

pourquoi ? les objets bougent, donc un objet peut cacher la reprojection du point et le fragment visible dans l'image précédente n'est pas le bon fragment. En gros, toutes les silhouettes des objets en mouvement vont avoir ce problème, ie tous les pixels de l'image ou la visibilité des surfaces change. Il va falloir détecter ces situations et modifier l'accumulation des résultats de l'étape courante. Il existe pleins de variantes de ces tests...

En résumé, le TAA peut se formuler assez simplement :

historique= 0
pour l'image i sur N,
    réaliser la ième étape de calculs intermédiaires pour chaque pixel de l'image,
    reprojetter le point visible par chaque pixel dans l'image précédente,
    si le point reprojetté correspond à la même surface :
      accumuler les résultats des étapes précédentes dans le pixel courant,
    sinon
        ??
afficher l'image courante.
l'image courante devient l'historique / l'accumulation des résultats précédents.

la qualité ou les défauts du TAA sont introduits par la partie notée ??, lorsque l'on ne connait pas l'historique du pixel...
le test de reprojection peut être approximatif lui aussi et introduire des erreurs dans l'accumulation.
Il y a une autre cause de défauts d'accumulation même lorsque la reprojection est correcte : le point reprojetté n'aura pas les coordonnées exactes du centre d'un pixel dans l'image précédente.

Comment détecter que le pixel reprojetté est valide / correct ? ie qu'il contient bien l'historique du pixel ?
    1. tests classiques sur les différences de normales et de profondeurs qui permettent de détecter une discontinuité,
    2. on pourrait aussi faire un test sur la couleur, mais c'est inutilisable avec des reflets, on pourrait stocker la couleur de base de l'objet, ou, plus simple, ses coordonnées de texture.

Que peut-on faire lorsqu'on ne connait pas l'historique d'un pixel ?
    1. rien ! le pixel n'a pas d'historique, il n'y aura pas d'accumulation.
    2. fabriquer une couleur plausible en utilisant (la distribution des couleurs) des pixels voisins...

Comment accumuler ou oublier l'historique ?
toutes les implémentations utilisent une moyenne exponentielle pour accumuler les résultats. Bizarrement, c'est assez intuitif : au lieu de moyenner le ième résultat avec l'historique, on pondère le nouveau résultat et l'historique :

\[ resultat = (1 - \alpha) \cdot historique + \alpha \cdot resultat \]

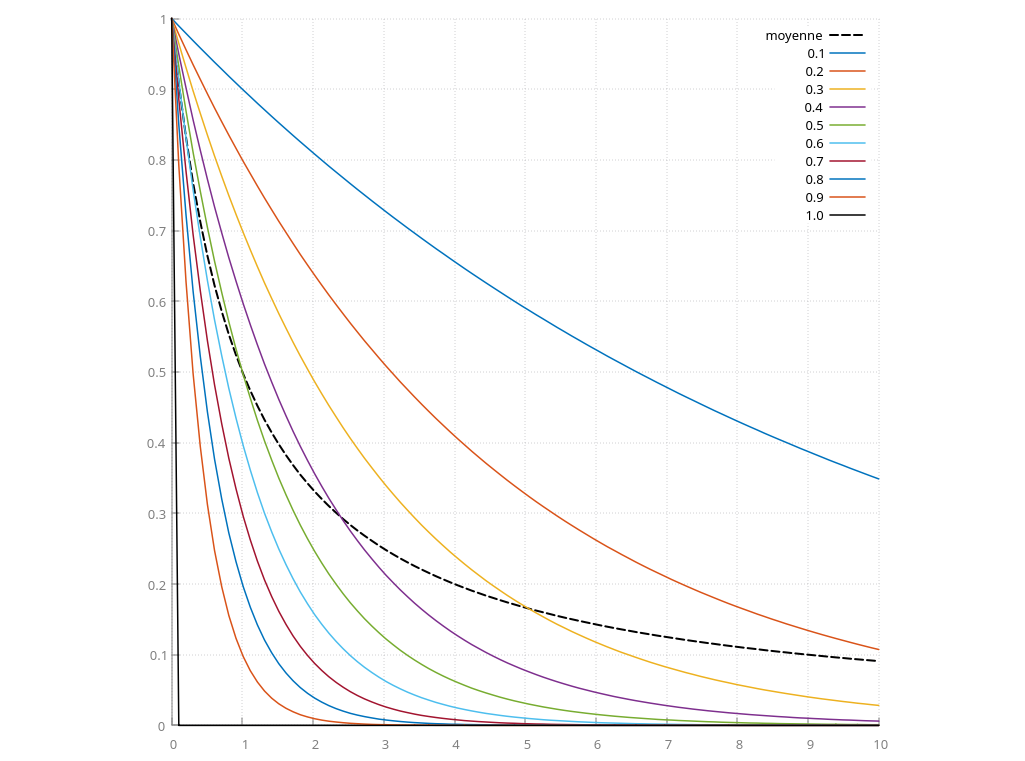
par exemple, voici le poids de la première valeur accumulée (notée \( x_0 \) au dessus) en fonction de \( \alpha \) et du nombre d'images accumulées / du temps. La courbe noire hachurée représente la pondération utilisée pour calculer une moyenne comme expliqué au-dessus \( \alpha= 1 / (n+1) \).

si \( \alpha \) est proche de 1, le résultat contient très peu d'historique, la pondération de la première valeur \( x_0 \) est déja à 0.1 pour l'image suivante lorsque \( \alpha= 0.9 \) et on oublie l'historique l'image suivante si \( \alpha= 1 \).
à l'inverse, si \( \alpha \) est faible, 0.1 par exemple, on accumule le résultat actuel avec les résultats précédents. et \( x_0 \) à encore une pondération de ~0.4 après 10 images accumulées...

exercice : quelle valeur de \( \alpha \) permet de calculer une moyenne ?
ou : pourquoi appele-t-on cette accumulation une moyenne exponentielle ?

la réponse se trouve, par exemple, dans "Amortized Super-Sampling", L. Yang, Siggraph 2009

pour calculer la moyenne de N valeurs, \( \alpha \) n'est pas constant dans le temps... mais toutes les implementaions de TAA utilisent des valeurs constantes (sauf dans la partie notée ??) ce qui veut dire qu'elles ne convergent jamais vers le résultat exact d'une moyenne ou d'une intégration... les explications et comment réduire l'erreur sont expliqués dans l'article précédent. (divulgachage de la réponse : il suffit de compter !)

question : combien d'images peut-on espérer accumuler ?
indications : s'il y a beaucoup de mouvements, il y aura beaucoup de discontinuités et les pixels correspondants n'auront pas d'historique. pour les autres, il est aussi probable que leur couleur change dans le temps, si une source de lumière bouge, s'ils passent à l'ombre d'un objet, etc... en pratique, il est assez difficile d'accumuler plus de 4 ou 8 images !

Partie 2 : comment ça se code ?

avant de vous lancer dans le code, passez un peu de temps à comprendre les différentes options qui sont résumées dans cet article (un peu trop) très complet :
"A Survey of Temporal Antialiasing Techniques" L. Yang, Eurographics 2020

oui, bien sur, TAA est surtout utilisé pour accumuler plusieurs échantillons par pixel pour réduire l'aliasing géométrique, mais la méthode est tellement générale que l'on peut l'utiliser pour presque tout qui nécessite de calculer une moyenne ou d'intégrer une fonction...

pour les curieux : anti aliasing géométrique avec TAA, "An excursion in Temporal Supersampling", M. Salvi, GDC 2016
pour les très curieux : la version apprentissage par le même auteur l'année suivante : "Deep Learning: The Future of Real-Time Rendering ?", M. Salvi, Siggraph course 2017
pour ceux qui veulent utiliser de l'apprentissage : "Minimal Convolutional Neural Networks for Temporal Anti Aliasing", K. Herveau, M. Piochowiak, C. Dachsbacher, HPG 2023

exercice 1 :
nettoyez votre code de rendu différé.

exercice 2 :
allouez une texture couleur supplémentaire 4 canaux GL_RGBA8 pour stocker l'historique. décomposez votre calcul d'éclairage direct avec 256 sources ponctuelles sur plusieurs images et additionnez les N valeurs successives dans l'historique.

vérifiez que sur une scène fixe, sans mouvement d'objet ou de camera, l'image converge vers le même résultat qu'avant de décomposer les calculs.
que se passe-t-il lorsque la camera bouge ? tout le problème va être de détecter et de corriger ces défauts d'accumulation.

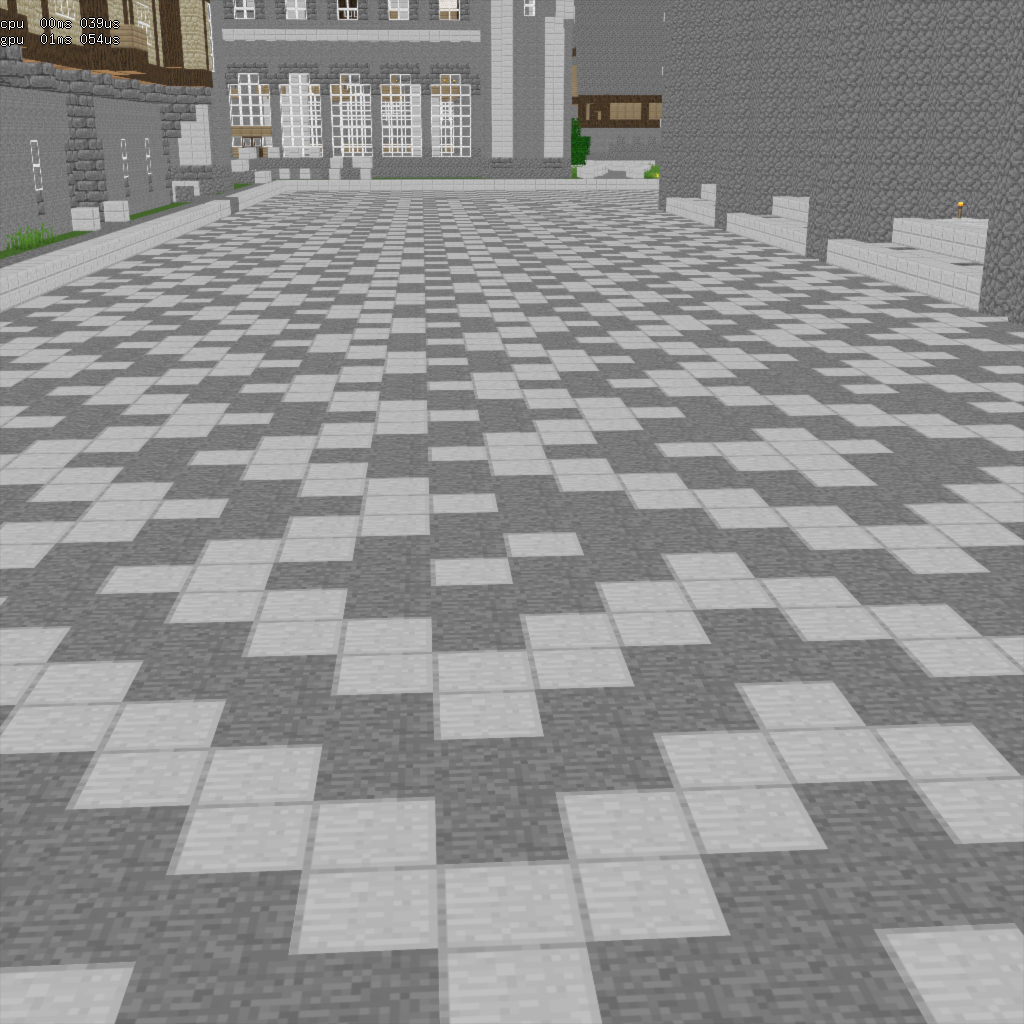
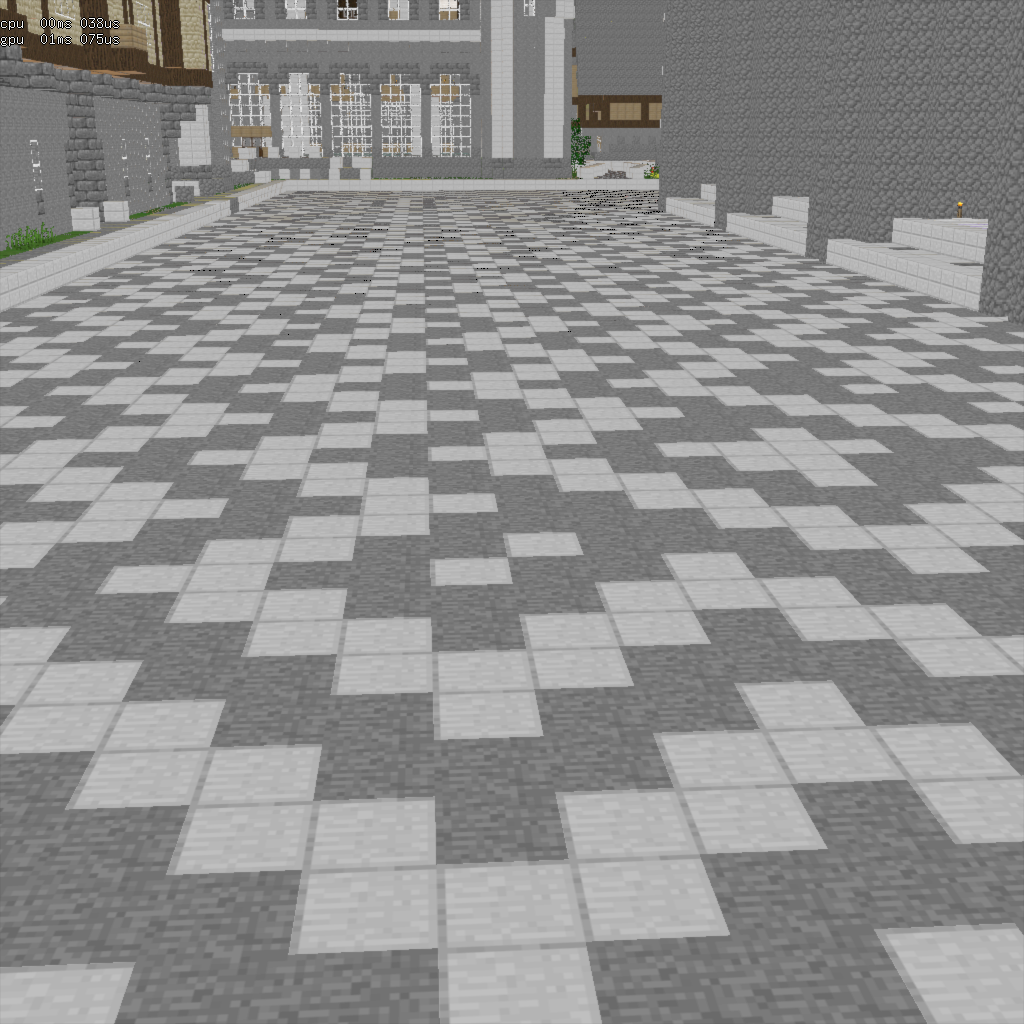
à gauche : scène fixe convergée, à droite : scène en mouvement, l'accumulation ne se fait pas sur le bon pixel...

rappel : vous pouvez copier une texture dans une autre avec glBlitFramebuffer(), mais il faut préparer un framebuffer :

init( ):
        // source         glGenFramebuffers(1, &src_framebuffer);         glBindFramebuffer(GL_READ_FRAMEBUFFER, src_framebuffer);         {             glFramebufferTexture(GL_READ_FRAMEBUFFER, GL_COLOR_ATTACHMENT0, src_texture, /* mipmap */ 0);             glReadBuffer(GL_COLOR_ATTACHMENT0);         }                 // copie
        glGenFramebuffers(1, &dst_framebuffer);
        glBindFramebuffer(GL_DRAW_FRAMEBUFFER, dst_framebuffer);
        {
            glFramebufferTexture(GL_DRAW_FRAMEBUFFER, GL_COLOR_ATTACHMENT0, texture, /* mipmap */ 0);
            GLenum buffers[]= { GL_COLOR_ATTACHMENT0 };
            glDrawBuffers(1, buffers);
        }

render( ):
        glBindFramebuffer(GL_READ_FRAMEBUFFER, src_framebuffer);
        glBindFramebuffer(GL_DRAW_FRAMEBUFFER, dst_framebuffer);

        // copie une région de 1024x1024 pixels...
        glBlitFramebuffer(0,0, 1024,1024, 0,0, 1024,1024, GL_COLOR_BUFFER_BIT, GL_NEAREST);

exercice 3 :
modifiez l'application pour stocker la transformation de l'image précédente. modifiez les shaders pour calculer les 2 transformations et lire la couleur du pixel reprojetté dans l'image précédente. Dans un rendu différé, il faut aussi créer une texture pour stocker la reprojection du pixel dans l'image précédente. utilisez une texture 2 canaux GL_RG16F.

indications : n'oubliez pas que les coordonnées de texture() sont entre 0 et 1, et que les coordonnées de texelFetch() et imageLoad() sont en pixels (ie entre 0 et largeur et 0 et hauteur). Pensez à utiliser la transformation Viewport(), elle sert exactement à ça !

rappel : après une multiplication par une matrice de projection, un point n'est plus réel mais homogène, pensez à retrouver le point réel en normalisant le point homogène, ie

vec4










      ph= matrix * vec4(p, 1); vec3 pp= ph.xyz / ph.w;

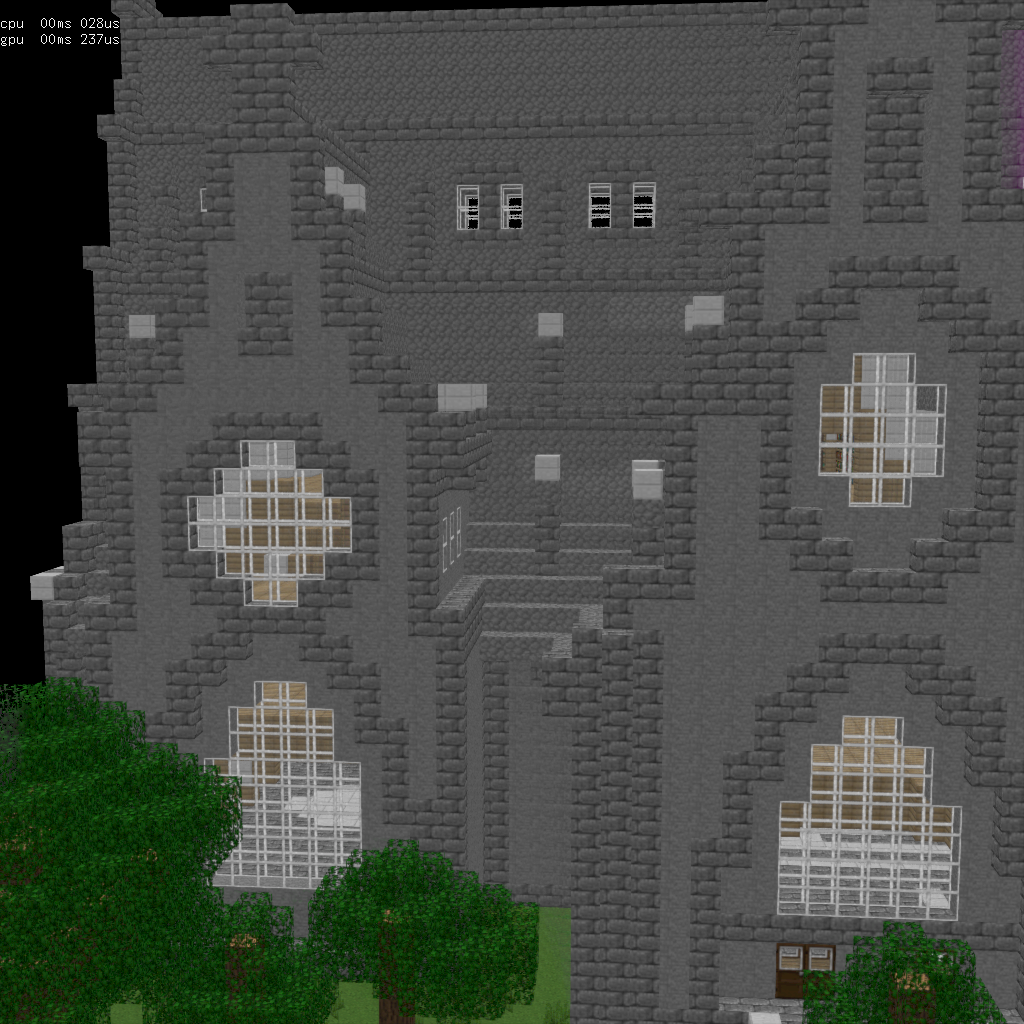
à gauche : scène fixe convergée, à droite : scène en mouvement, l'accumulation se fait maintenant sur le bon pixel...
sauf sur le bord droit ou les points n’étaient pas visibles dans l'image précédente (les pixels sont marqués en violet)

exercice 4 : c'est peu flou non ?
relisez "Amortized Super-Sampling" pour comprendre pourquoi accumuler l'historique et le pixel filtre / floute le résultat.

indications : en plus des solutions proposées dans l'article, il y a tout simplement la possibilité de désactiver le filtrage et l'interpolation de la texture qui stocke l'historique ! il y a 2 solutions pour lire une texture sans interpolation :

1. soit paramétrer la texture pour désactiver l'interpolation avec glTexParameter(GL_TEXTURE_2D, GL_XXX_FILTER, GL_NEAREST), à placer après le code de création de la texture dans init(), ie make_vec3_texture(); et utiliser texture() dans le shader,
2. soit utiliser texelFetch() dans le shader.

pour les curieux : vous pouvez tester avec un filtre de meilleure qualité que le filtre bilinéaire du matériel. un filtre bicubique par exemple. on peut soit lire 16 pixels dans l'image pour filtrer, ce qui est assez (trop) lent... soit utiliser le filtre bilinéaire du matériel pour accélérer le calcul du filtre bicubique... en ne faisant que 4 ou 5 accès filtrés à la texture... cf "Bicubic Filtering in Fewer Taps"

ou pour les très curieux, on peut aussi estimer l'erreur commise par le filtre bilinéaire et la corriger, c'est encore plus rapide (en 3 accès filtrés à la texture) l'idée est présentée par M. Drobot, dans "HRAA" en 2014, slides 59-95. c'est la méthode d'anti aliasing utilisée par FarCry 4. cf l'article original "An Unconditionally Stable MacCormack Method" A. Selle, 2008 pour les détails complets sur la méthode de correction d'erreur.

exercice 5 : c'est pas trop lisse non ?
Habituellement, la fragmentation ne teste qu'un seul point par pixel (le centre du pixel) et n'évalue qu'un seul fragment shader. Pour les pixels sur lesquels se projettent plusieurs triangles, un seul triangle sera donc testé et évalué, et la couleur calculée pour ce pixel ne sera pas vraiment représentative de sa "vraie" couleur (ie la moyenne des couleurs des triangles). La fragmentation / rasterization matérielle peut tester plusieurs points par pixel, ie plusieurs échantillons, et calculer une meilleure estimation de la couleur moyenne de ces échantillons. La plupart des cartes graphiques supportent jusqu'à 8 ou 16 points nativement. Exécuter les fragments shaders pour chaque point testé est vraiment très long et ce mode d'anti-aliasing, le FSAA (Full Screen AA) n'est pas utilisé en pratique (sauf peut être dans un mode photo non interactif...). Les cartes proposent aussi une version approchée plus rapide : le MSAA (Multi Sample AA) qui n'exécute les fragments shaders qu'une fois par triangle touché par un point. Cette optimisation du FSAA suppose que la couleur du triangle est constante par pixel. Il n'y a en pratique que 2 ou 3 triangles qui touchent quelques pixels le long des arêtes ou sur les sommets des triangles. A l'intérieur des triangles, il n'y a bien sur qu'un seul triangle. En résume, la quasi totalité des pixels de l'image (>90%) n'exécute qu'une seule fois le fragment shader. Cette solution, le MSAA est vraiment plus efficace, sans introduire trop de défauts par rapport à la référence. Mais son utilisation est limitée au rendu direct / forward. Lorsque l'on utilise un rendu différé, il est très simple de reproduire le FSAA, ie d'évaluer la couleur de tous les points. Par contre, reproduire MSAA est plus délicat, il faudrait trier les triangles touchés par les points testés par la fragmentation et n'exécuter que le bon nombre de shaders, par pixel... ce qui produit une exécution très incohérente qui est donc particulièrement lente. En bref, le MSAA n'est pas trop adapté au rendu différé... (sans parler du volume des textures qui stockent 4 ou 8 valeurs au lieu d'une seule. La mémoire disponible pour stocker des choses plus intéressantes (comme des textures ou de la géométrie...) est réduite elle aussi).

Pour gagner du temps et simplifier la réalisation, on va utiliser TAA et un seul point aléatoire par pixel et par image. Il faut configurer le pipeline graphique pour tester un point différent du centre du pixel. cf les extensions propriétaires amd et nvidia par exemple. Ou, on peut tout simplement déplacer l'espace projectif d'une fraction de pixel, ce qui revient au même (oui, tous les pixels testent le même point au lieu de tester le centre). Il suffit d'appliquer une translation sur le plan xy dans le repère projectif : Translation(x / image_width, y / image_height, 0) avec x et y, 2 nombres aléatoires compris entre -0.5 et 0.5.

Vérifiez que lorsque la scène est fixe vous obtenez une version anti-aliassée de l'image, ie que vous calculez vraiment la moyenne de 16 échantillons, par exemple. (ie quelles sont les valeurs d'alpha dans ce cas ?) Que faire pour la 17 ieme image ?
Quel est le défaut de cette solution lorsque la camera ou la scène bouge ? comment régler alpha dans ce cas ?

exercice 6 : et les textures semi-transparentes ?
cf "Stochastic Transparency" E. Enderton, Siggraph I3D 2010

même principe que l'exercice précédent, on remplace une intégration par TAA.
il suffit d'intégrer l'opacité dans la passe de construction du GBuffer. et... c'est tout, on obtient magiquement la transparence des objets.

dans le fragment shader qui construit le GBuffer, il y a probablement un test sur la transparence de la texture :

vec4 color= texture( diffuse, texcoords );
if(color.a < 0.3)
discard;

il suffit de rendre ce test aléatoire pour détruire (ou pas) le fragment le bon nombre de fois (ie color.a donne la proportion) afin de rendre l'objet transparent ou opaque.

rappel : construire un générateur de nombre aléatoire est aussi simple qu'une fonction de hachage, cf CRNG32 dans "Rendu et générateurs de nombres aléatoires"

"Stochastic Transparency" intégrée "automatiquement" par TAA, la camera est au milieu d'un arbre (!?)
et observe l'intérieur de la maison à travers plusieurs surfaces semi-transparentes.

exercice 7 : peaufinage...
comment éliminer ou en tout cas estomper les défauts de TAA ?

relisez le résumé des techniques de TAA et expérimentez.
par exemple, ajuster alpha en fonction de la vitesse de déplacement marche plutôt bien...

on peut également assez facilement détecter les discontinuités (en analysant le voisinage 3x3 des pixels) sur les normales (à gauche) et la profondeur (à droite) ou la vitesse de déplacement :

à gauche : discontinuités sur les normales dans un voisinage 3x3, à droite : discontinuités sur la profondeur dans un voisinage 3x3...
on remarque que les discontinuités détectées dans les 2 cas sont complémentaires :
ie le test sur les normales ne détecte pas un changement de profondeur comme autour des fenêtres sur la façade,
alors que le test sur la profondeur le détecte. et symétriquement, le test sur la profondeur ne détecte pas les changements d'orientation...

exercice 8 : et les textures opaques ?
il existe plusieurs paramètres de filtrage des textures : GL_LINEAR, GL_NEAREST, GL_LINEAR_MIPMAP_LINEAR, GL_ANISOTROPY, etc pourquoi ?
ces filtres classiques sont-ils exacts ?
pourrait-on utiliser TAA pour remplacer les filtres classiques ?
comment ? quel serait l’intérêt ?

pour les curieux : monte carlo, importance sampling et filtrage de texture, cf M. Salvi 2024 (encore lui !!) "Stochastic Texture Filtering"
suivi de "Improved Stochastic Texture Filtering Through Sample Reuse" B. Wronski, M. Pharr, T. Akenine-Moller, 2025

quizz ! filtres GL_LINEAR_MIPMAP_LINEAR + ANISOTROPY 8x, ou GL_NEAREST, ou GL_NEAREST + TAA ?