Comment reproduire le type de reflet que l'on peut observer dans cette expérience ?
 |  |  |
Le modèle de Lambert, permet de reproduire le comportement de gauche, un "reflet" diffus, les coefficients de Fresnel reproduisent un miroir, le comportement de droite, un reflet spéculaire. Comment contrôler le reflet dans le cas intermédiaire ?
modèles empiriques
B. Phong en 1975 propose de représenter le reflet comme un cone plus ou moins concentré (avec un angle d'ouverture plus ou moins grand) aligné dans la direction miroir. Ce qui semble raisonnable sur l'exemple illustré ci-dessus. Mais qui a pourtant un gros défaut : un "vrai" reflet se déforme en fonction de l'incidence... Le reflet du modèle de Phong reste parfaitement symétrique : ce n'est pas trop choquant sur des objets, mais c'est assez bizarre sur de grandes surfaces, comme un sol, une route, l'ocean, etc.
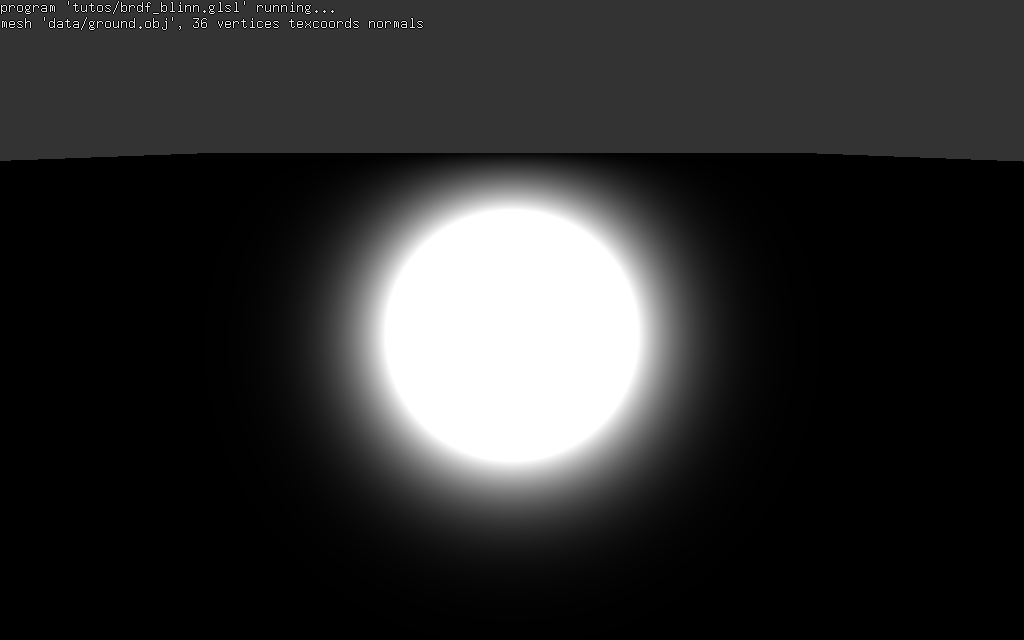 |  |
| modèle Phong | modèle Blinn - Phong |
pour vous convaincre, cherchez des photos d'ocean vu d'avion, ou des photos prises apres la pluie en ville avec les reflets de toutes les lumieres...
J. Blinn en 1976, reformule le modèle de B. Phong pour mieux reproduire l'étirement des reflets lorsque la lumière est incidente avec un angle d'incidence important. L'idée est relativement simple : quelle devrait être la direction de la normale de la surface pour produire un reflet "miroir" entre les directions \( \vec{o} \) et \( \vec{l} \) ?
indications : on peut calculer la direction miroir de \( \vec{l} \) par rapport à la normale. \( \vec{l} \) et \( \vec{m} \) deviennent symétriques par rappport à la normale : le même angle les sépare de la normale. La normale est le bisecteur de \( \vec{l} \) et \( \vec{m} \).
réponse :
\[ \vec{h}= \frac{\vec{o} + \vec{l}}{|| \vec{o} + \vec{l} ||} \]
le bisecteur des 2 vecteurs \( \vec{l} \) et \( \vec{o} \) . La direction \( \vec{o} \) devient symétrique de \( \vec{l} \) par rapport à \( \vec{h} \). Si la normale de la surface est orientée comme \( \vec{h} \), \( \vec{l} \) est la direction miroir de \( \vec{o} \). Et plus \( \vec{h} \) est loin de la normale en p, plus l'observateur est loin du reflet miroir de \( \vec{l} \).
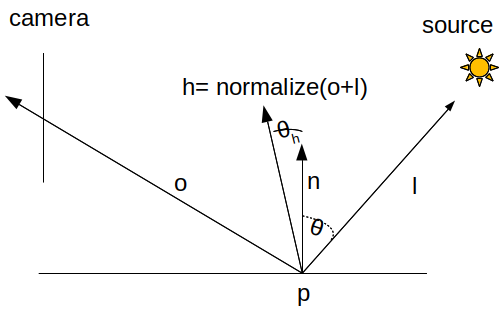
Ne reste plus qu'une question : comment controler la taille, la concentration du reflet ? Il fallait une fonction rapide à calculer (en 1976 les machines n'etaient pas tout à fait les mêmes...) et qui décroit plus ou moins vite vers 0 en fonction d'un paramètre...
et c'est \( \cos^\alpha \theta_h \) qui à gagné. mais pas tout à fait :
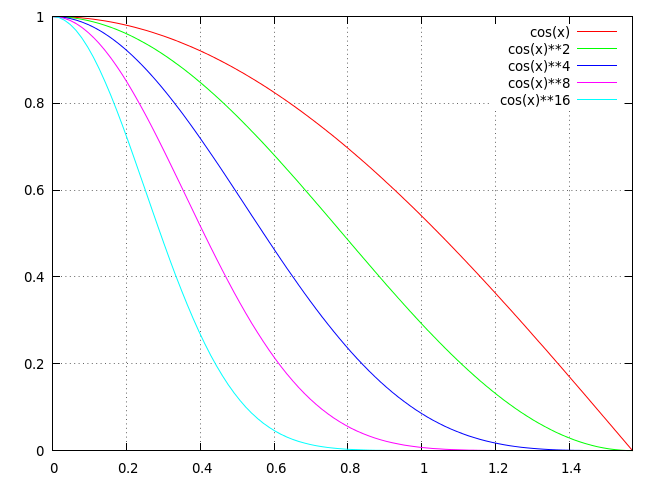
l'exposant permet bien de controler la taille du reflet, la fonction décroit vers 0 plus ou moins vite, mais plus le reflet est petit, moins il est intense, ce qui est plutot génant... la fonction doit vérifier une autre propriété : elle doit etre normalisée, son intégrale sur les directions de l'hemisphère doit être égale à 1, quelque soit la taille du reflet, la même quantité de lumière est réfléchie sur l'ensemble des directions : \( \frac{\alpha +1}{2\pi} \int \cos^\alpha \theta_h \, d\omega = 1\)
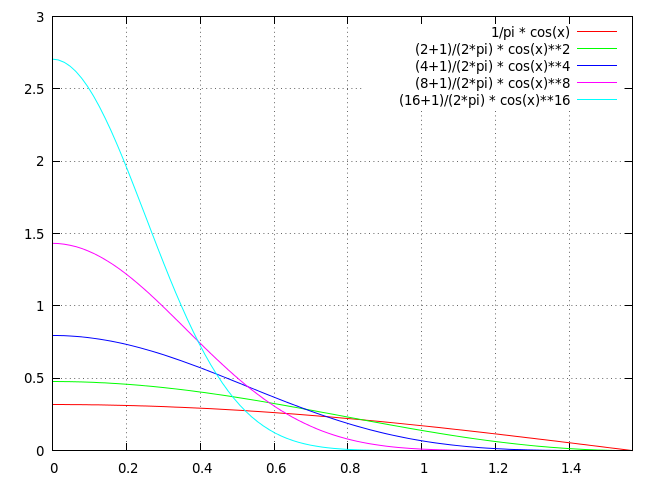
Mais si on utilise cette fonction comme brdf, il se passe autre chose : la matière réfléchit plus de lumière qu'elle n'en reçoit... c'est encore un problème de normalisation. Il faut s'assurer que pour une direction \( \vec{l} \) la somme de la lumière réfléchie \( f_r(\vec{l}, \vec{o}) \cos \theta_i \) est inférieure ou égale à 1 :
\[ \int f_r(\vec{l}, \vec{o}) \cos \theta_i d\omega_i = 1 \]
remarque : lorsqu'un modèle de matière vérifie cette condition de normalisation, on dit qu'il conserve l'énergie.
Pour le modèle Blinn - Phong, il n'existe pas de solution parfaite, c'est un compromis, les calculs sont rapidement décrits par F. Giesen et fournissent un résultat simple :
\[ f_r(\vec{o}, \vec{l})= \frac{\alpha+8}{8\pi} \cos^\alpha \theta_h\]
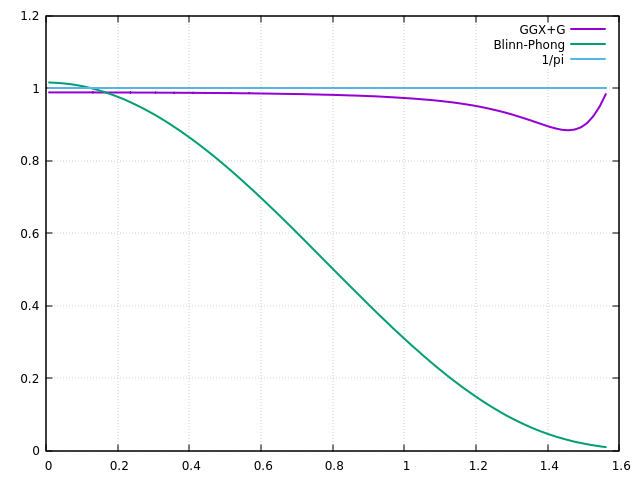
et voila la quantité de lumière réfléchie en fonction de \( \theta_l \), pour les 3 versions : modèle diffus (courbe bleue), modèle normalisé (courbe rouge) et modèle conservatif (courbe verte) :
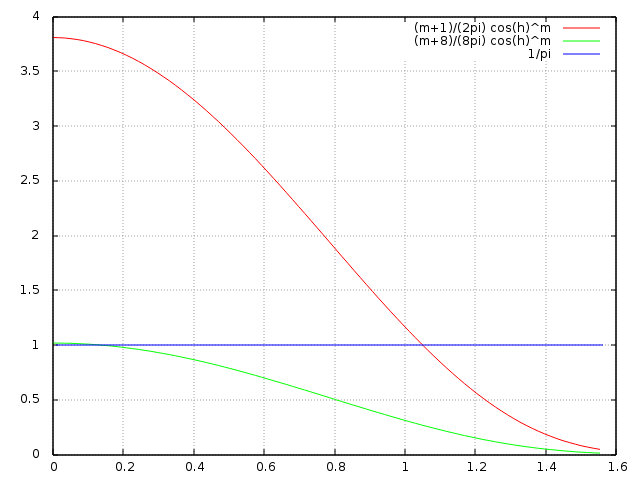
Ce modèle, Blinn - Phong conservatif et normalisé, est très simple à calculer, se comporte correctement, mais l'intensité de ses reflets diminue lorsque l'incidence de la lumière augmente, ce qui ne correspond pas vraiment à ce que l'on peut observer dans la nature...
modèles physiques
Pour faire mieux, il va falloir regarder les travaux des physiciens... Dans les années 1960, Torrance et Sparrow proposent une formulation permettant de prédire la propagation d'une onde electro-magnétique, comme la lumière (ou une onde radar...) sur une surface rugueuse et pas parfaitement lisse comme dans le cas des coefficients de Fresnel. Ces travaux sont utilisés pour la première fois comme modèle de reflet en 1982 par Cook (qui travaillait alors chez Pixar) et le meme Torrance.
Ce modèle a été utilisé pour produire les premiers films et court-métrages de Pixar (cf Luxo Jr en 1986 et Toy Story 1 en 1995), puis reformulé en 2007, comparé à des mesures en 2012, puis serieusement nettoyé en 2014. Depuis, la quasi totalité des productions utilisent des variantes du même modèle, cf Burley 2015.
voici les articles principaux :
- Cook - Torrance 1982 : modèle à microfacettes dérivé de Torrance - Sparrow 1967, surface rugueuse opaque,
- Walter 2007 : reformulation du modèle de Cook - Torrance, utilisation de la distribution GGX et de sa normalisation exacte, surface rugueuse opaque ou transparente,
- Burley 2012 : comparaison mesures / modèles, reparamétrisation "intuitive" des paramètres, séparation des métaux des autres matières, modèle Disney / "Principled BRDF",
- Heitz 2014 : normalisation, conservation de l'énergie et validation des modèles à microfacettes, slides
- Burley 2015 : simplification, intégration des validations de Heitz 2014, diffusion
modèles à microfacettes
L'idée de ces travaux est de considérer que la surface géométrique de l'objet est composée d'un ensemble de facettes miroir microscopiques. Elles ne sont pas observables à notre échelle mais sont responsables de la forme et de l'intensité du reflet. Au lieu de les modéliser explicitement / géométriquement, elles sont représentées par quelques statistiques : distribution d'altitude et distribution d'orientation.
Un modèle à microfacettes se présente classiquement sous cette forme :
\[ f_r(\vec{o}, \vec{l})= \frac{F(\vec{o}, \vec{h}) \, D(\vec{h}) \, G_2(\vec{o}, \vec{l}, \vec{h}) }{4 |\vec{n} \cdot \vec{o}| |\vec{n} \cdot \vec{l}|} \]
Le terme \( F \), le coefficient de Fresnel, représente le reflet crée par une facette, \( D \) correspond au nombre de facettes orientées dans la direction \( \vec{h} \) et qui créent l'intensité du reflet (plus il y a de micro-facettes orientées dans la bonne direction, plus le reflet est intense). Le reste, \( G_2 \) et le cosinus \( |\vec{n} \cdot \vec{o}| \) permettent de normaliser \( D \) pour garantir la conservation d'énergie. C'est au final, le même raisonnement que tout à l'heure, pour normaliser le modèle Blinn-Phong :
\[ f_r(\vec{o}, \vec{l})= \frac{F(\vec{o}, \vec{h}) \, D(\vec{h})}{\cos \theta} \left( \frac{G_2(\vec{o}, \vec{l}, \vec{h}) }{4 |\vec{n} \cdot \vec{o}|} \right) \]
Il ne reste plus qu'à trouver quelles fonctions utiliser pour \( D \) et \( G_2 \). Les fonctions sont plus complexes que les modèles précédents mais se calculent sans trop de problèmes.
D et G
remarque : les détails complets sont dans "Understanding the Masking-Shadowing Function in Microfacet-Based BRDFs" Heitz 2014
Le premier changement est la fonction qui décrit la concentration du reflet, au lieu d'une puissance de cosinus, c'est une fonction issue de travaux en physique qui est couramment utilisée, en grande partie parce qu'elle permet de mieux reproduire les reflets des metaux. C'est le paramètre \( \alpha \) qui permet de controler la rugosité de la surface et la concentration du reflet : 0 pour une surface parfaitement lisse, et 1 pour une surface matte, "parfaitement" rugueuse :
\[ D( \vec{h} ) = \frac{\chi^+(\vec{h} \cdot \vec{n})}{\pi \alpha^2 \cos^4 \theta_m \left( 1 + \frac{\tan^2 \theta_h}{\alpha^2} \right)^2 }, \textrm{ cf Heitz 2014, eq 71}\\ \]
Cette version de \( D \) s'appelle GGX dans la communauté image et TR pour les physiciens (d'après les travaux de Trowbridge - Reitz)
L'autre intéret de cette fonction est que l'on peut la normaliser et obtenir un modèle qui conserve l'énergie :
\begin{eqnarray*} G_2( \vec{o}, \vec{l}, \vec{h} ) & = & \frac{\chi^+(\vec{o} \cdot \vec{h}) \chi^+(\vec{l} \cdot \vec{h})} {1 + \Lambda(\vec{o}) + \Lambda(\vec{l})}, \textrm{ cf Heitz 2014, eq 99}\\ \textrm{ avec}& : &\\ \Lambda(\vec{\omega}) & = & - \frac{1}{2} + \frac{1}{2} \sqrt{1 + \alpha^2 \tan^2 \theta}, \textrm{ cf Heitz 2014, eq 72}\\ \textrm{ et}& : &\\ \chi^+(x) & = & 0 \textrm{ si } x < 0\\ & = & 1 \textrm{ sinon } \end{eqnarray*}
Cette manière de normaliser \( D \) vient des travaux de Smith et ce modèle de micro surface / micro facettes est appelé Smith - GGX.
Ces formulations ne sont pas très intuitives, mais la fonction \( D \) représente les normales d'une hemisphère déformée et projettées sur la surface... voici quelques exemples tirées de "Sampling the GGX Distribution of Visible Normals" , Heitz 2018 :
une hemisphère (non déformée) produit une distribution de normales (NDF) constante (illustré par la sphère à droite) 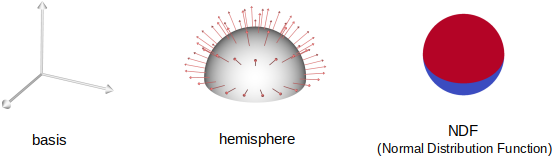
si l'hemisphère est déformée par un Scale(x, y, z), on modifie en même temps les directions des normales et la NDF se concentre plus ou moins autour de la normale de la surface, ce qui permet de créer un reflet plus ou moins concentré : 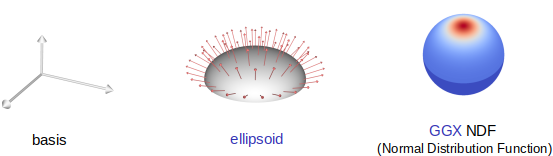
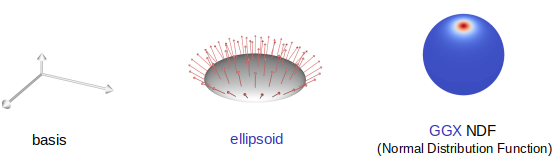
les directions des normales sont utilisées pour perturber la surface lisse, ie créer les micro facettes et leur orientation, c'est à dire la fonction \( D \) : 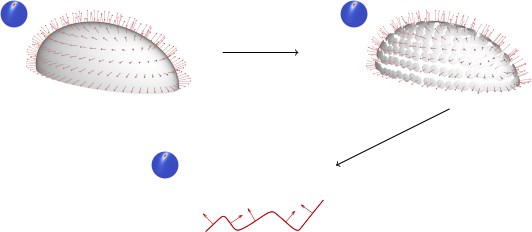
par contre, il reste un dernier détail à régler : peut on prédire la reflexion de la lumière sur les micro facettes uniquement avec leur orientation ? dans l'exemple suivant, on suppose que l'on a 3 micro facettes / orientations, la fonction \( D \) est donc identique pour les 2 exemples de micro surfaces : 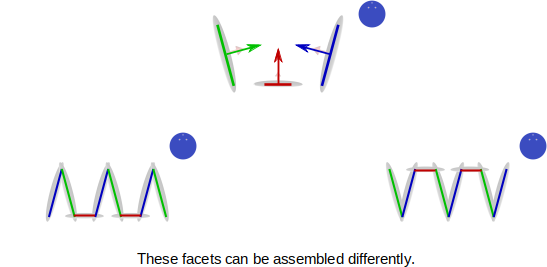
et selon la forme de la micro surface, la lumière est réfléchie différement, c'est le role de la fonction \( G \) (en plus de normaliser tout ca...) : 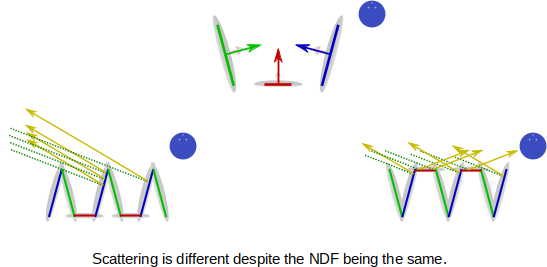
du coup, il y a plusieurs versions de la fonction \( G \), en fonction du type de micro surface, par exemple eq 98 et eq 99 ainsi que la discussion de la section 6 de Heitz 2014.
Mais, il ne faut pas oublier que D et G sont un couple de fonctions, on ne peut pas choisir une fonction G indépendement de D : G sert aussi à normaliser D (en plus de construire la micro surface).
et ca conserve l'énergie, au moins ?
pas trop mal...
et alors ? c'est quoi le modèle de matière ?
On vient de voir rapidement comment décrire le comportement de la lumière dans 3 cas particuliers : parfaitement diffus, parfaitement spéculaire (reflet par un miroir lisse) et "reflets" intermédiaires sur une surface rugueuse, mais il reste une question, comment représenter une vraie matière ??
La solution se trouve dans les travaux de Burley en 2012 et 2015 qui a analysé des mesures de vraies matières et proposé une manière intuitive de les décrire, cf
- "Physically Based Shading at Disney" Burley 2012,
- "Extending the Disney BRDF to a BSDF with Integrated Subsurface Scattering" Burley 2015.
Le premier constat est sans surprise : d'un cote, il y a les métaux avec un reflet décrit par un modèle à micro facettes et les coefficients de Fresnel, et de l'autre, le reste... les non métaux (les diélectriques). Ils sont décrits par deux termes : une reflexion diffuse pondérée par les coefficients de transmission de Fresnel ainsi qu'une réflexion spéculaire (éventuellement avec des microfacettes). Ce qui correspond bien aux comportements prédits par les équations de Fresnel (cf indice de réfraction réel ou complexe / imaginaire et les reflexions diffuses ou spéculaires).
\begin{eqnarray*} \textrm{(diélectrique) } f_d(\vec{o}, \vec{l}) & = & (1 - F) \cdot \frac{\textrm{diffuse color}}{\pi} + F \cdot \frac{ D \, G }{4 |\vec{n} \cdot \vec{o}| |\vec{n} \cdot \vec{l}|} \\ \textrm{(métal) } f_m(\vec{o}, \vec{l}) & = & (1 - F) \cdot \textrm{black} + F \cdot \frac{ D \, G }{4 |\vec{n} \cdot \vec{o}| |\vec{n} \cdot \vec{l}|} \end{eqnarray*}
Les indices de réfraction sont bien sur différent dans les deux cas. Pour la rugosité de la micro surface, on peut utiliser la même valeur, ou pas...
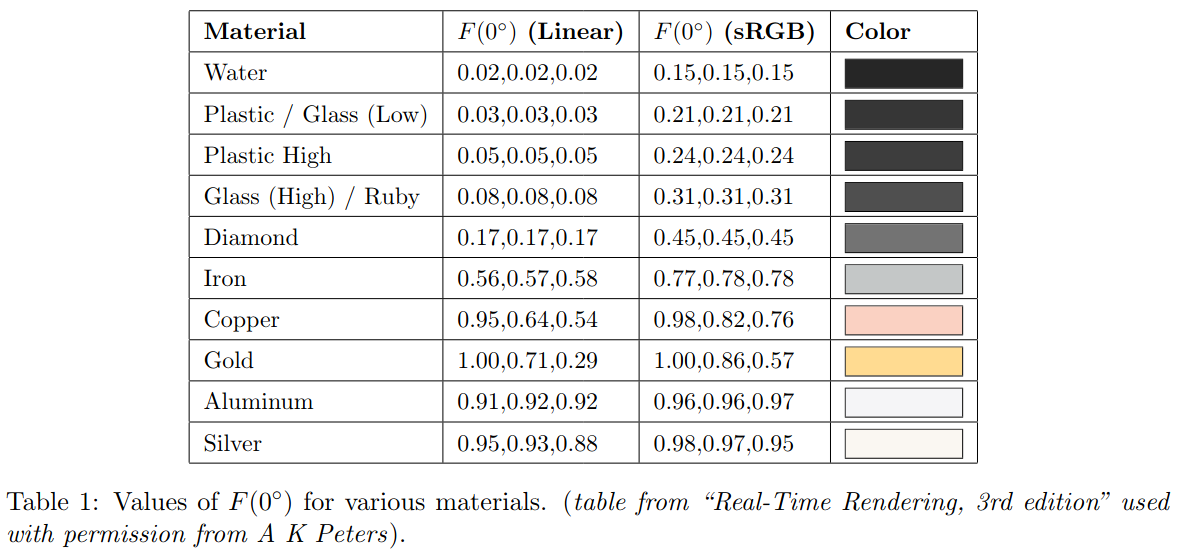
Burley propose de représenter une matière par 3 paramètres : métal, couleur et rugosité. Un autre travail important réalisé par Burley est d'avoir remplacé les grandeurs physiques par des valeurs plus simples à manipuler comprises entre 0 et 1... Par exemple, l'indice de réfraction n'apparait pas directement, il est "remplacé" par une couleur qui est utilisée comme \( F_0 \) pour évaluer les coefficients de Fresnel. Voici quelques exemples :
La brdf se présente comme l'interpolation entre 2 termes : réflexion dielectrique et réflexion métallique en fonction de la valeur de métal. Lorsque métal vaut 1, le poids du terme dielectrique est à 0, et inversement. La couleur est utilisée soit par le terme diffus de la réflexion dielectrique, soit comme valeur de \( F_0 \) pour évaluer les coefficients de Fresnel du modèle métallique.
metal est normalement un terme binaire, 0 ou 1 : soit la matière est un métal, soit pas... Dans la nature, il n'existe pas d'intermédiaire, mais pour des raisons pratiques, on se retrouve souvent avec des valeurs qui varient entre 0 et 1, il faut donc ajuster les parametres pour éviter les surprises, ie on ne veut pas utiliser couleur à la fois comme \( F_0 \) et comme couleur diffuse.
Une solution courante est détaillée dans les annexes de glTF 2. La couleur du terme diffus est interpolée entre couleur et noir en fonction de metal (rappel : les métaux n'ont pas de diffusion, uniquement une réflexion spéculaire de surface), et le terme spéculaire / les coefficients de Fresnel sont interpolés entre 0.04 (valeur moyenne pour \( F_0 \) pour les non métaux, cf Table 1 au-dessus) et couleur en fonction de metal. Et les deux micro surfaces utilisent la même rugosité. Burley propose aussi d'utiliser le carré de la rugosité comme paramètre des micro surfaces.
\begin{eqnarray*} f_r(\vec{o}, \vec{l}) & = & (1 - \textrm{metal}) \cdot f_d(\vec{o}, \vec{l}) + \textrm{metal} \cdot f_m(\vec{o}, \vec{l})\\ \textrm{diffuse color} & = & (1 - \textrm{metal}) \cdot \textrm{base color} + \textrm{metal} \cdot \textrm{black}\\ F_0 & = & (1 - \textrm{metal}) \cdot 0.04 + \textrm{metal} \cdot \textrm{base color}\\ \alpha & = & \textrm{roughness}^2 \end{eqnarray*}
La suite, comment écrire les shaders qui évaluent tout ca, et comment simplifier les expressions sont dans : shader et brdf
et c'est bon, on a tout là ?
ben non, pour le moment on peut décrire des surfaces opaques simples, toutes propres, mais il est souvent nécessaire d'ajouter des éraflures, une couche de vernis, de rouille, de poussière, etc... et pour certaines matières, on voudrait représenter une distribution de normales moins continue, pour représenter des paillettes ou une structure...