on vient de voir dans le cours comment calculer l'intersection
d'un rayon avec un plan ou avec une sphère. ça marche plutôt bien,
mais si on souhaite créer un objet avec un logiciel 3d comme Blender,
on ne pourra pas l'utiliser pour calculer une image. la plupart
des logiciels de modélisation 3d enregistrent uniquement des
triangles. mais il n'est pas trop difficile de calculer
l'intersection entre un rayon et un triangle...
après tout, un triangle n'est qu'un morceau de plan délimité par 3 sommets. on sait déjà comment calculer le point d'intersection du rayon avec un plan, il ne reste plus qu'à vérifier que le point est aussi à l'intérieur du triangle !
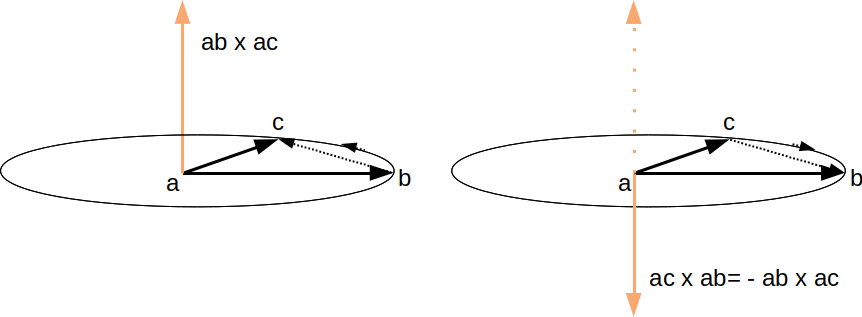
une solution consiste à vérifier que le point est du bon coté de
chaque arête du triangle. on va utiliser une propriété du produit
vectoriel : selon l'ordre des vecteurs, le résultat n'est pas
orienté de la même manière !

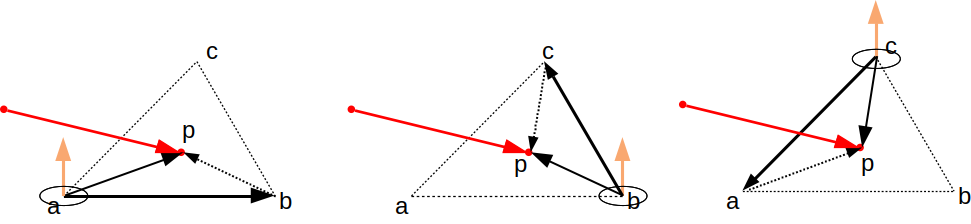
le schéma permet de vérifier : si on calcule le produit des
vecteurs ab et ac, ie de ab vers ac (noté ab x ac), on obtient le
vecteur orienté vers le haut. si on calcule le produit dans
l'autre sens, de ac vers ab (noté ac x ab), le résultat aussi est
orienté dans l'autre sens.
en pratique, ca veut aussi dire que le triangle abc n'est pas
orienté dans le même sens que le triangle acb. un triangle abc est
orienté comme le produit de ses 2 aretes : ab et ac. le triangle
abc est donc orienté comme le produit de ab vers ac et le triangle
acb est orienté comme le produit de ac vers ab.
c'est cette propriété que l'on va utiliser pour vérifier que le
point est du "bon" coté de chaque arête du triangle. par exemple,
pour l'arếte ab, le point p peut se trouver à l'intérieur du
triangle ou pas. c'est l'orientation du triangle abp qui permet de
décider :
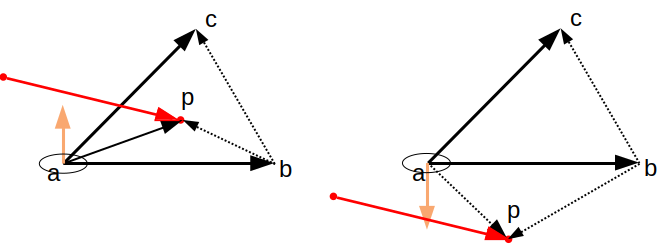
on va donc tester 3 triangles, un par arête. si les 3 triangles
abp, bcp, et cap sont orientés comme le triangle abc, le point est
du bon coté de chaque arête et il est à l'intérieur du triangle.
sinon, il est du mauvais coté d'une arête et donc, à l'extérieur
du triangle :
il ne reste plus qu'à comparer les orientations de 3 vecteurs
pour écrire le test ! et on sait déja que l'on peut utiliser le
produit scalaire de 2 vecteurs pour comparer leur orientation, ie
u . v sera positif si les vecteurs u et v sont orientés dans le
même sens et négatif sinon.
on peut maintenant écrire le test pour une arête : dot()
permet de calculer le produit scalaire et cross()
le produit vectoriel.
pour tester p par rapport à l'arête ab :
cross( Vector(a, b),
Vector(a, p) ) ce qui s'écrit directement :
Vector abc= cross(
Vector(a, b), Vector(a, c) );
// orientation du triangle abc : ab x ac
Vector abp= cross( Vector(a, b),
Vector(a, p) ); // orientation du triangle
apb : ab x ap
if(dot(abc, abp) <
0)
// comparaison des
orientations
return false;
// le point p est du mauvais coté de l'arete ab !
...
il ne reste plus qu'à recommencer pour les arêtes bc et ca. on
peut aussi éviter de calculer 3 fois l'orientation du triangle
abc...
le test complet va ressembler à :
bool intersect( /* rayon */
const Point& o, const Vector& d, const float tmax, /*
triangle */ const Point& a, const Point& b, const
Point& c )
{
// on commence par calculer la
normale du triangle, ie son orientation, ab x ac
Vector n= cross( Vector(a, b),
Vector(a, c) );
//
intersection du plan (a, n) avec le rayon (o, d) float t= dot(n, Vector(o,
a)) / dot(n, d); if(t < 0 || t > tmax)
return
false; // l'intersection n'est pas valide,
soit derriere la camera soit trop loin // point d'intersection avec
le plan Point p= o + t*d; // tester le triangle abp /
orientation des aretes ab et ap Vector abp= cross( Vector(a,
b), Vector(a, p) ); if(dot(n, abp) < 0)
return
false; // p est à l'extérieur de l'arête ab // tester le
triangle bcp / orientation des aretes bc et bp
...
// tester le triangle cap
/ orientation des aretes ca et cp
...
// le point est du bon coté
des 3 aretes, il est donc à l'intérieur du triangle !
}
read_positions() définie dans
mesh_io.h. #include "mesh_io.h"
std::vector<Point> positions;
if(!read_positions("data/robot.obj", positions))
return "erreur";
for(unsigned i=
0; i +2 < positions.size(); i += 3){ // triangle abc Point a= positions[ i ]; Point b= positions[ i +1 ];
Point c= positions[ i +2 ];
...
}// parcours les triangles for(unsigned i= 0; i < positions.size()/3;
i++){ // triangle abc Point a= positions[ 3*i ]; Point b= positions[ 3*i +1
]; Point c= positions[ 3*i +2
]; ...
}