Invariance principle for the random walk in random environment
Nov 1, 2022·
 ·
1 min read
·
1 min read
Armand Bernou
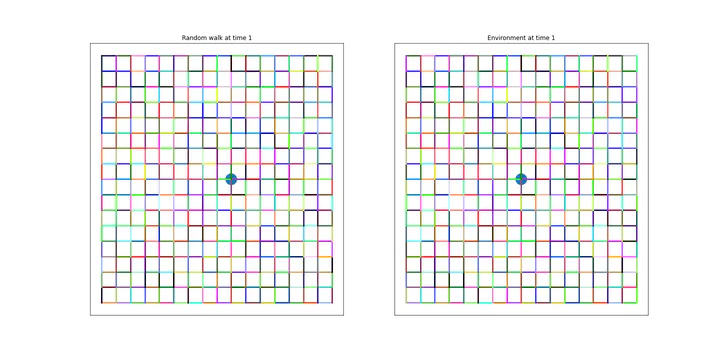 Image credit: Armand Bernou
Image credit: Armand Bernou
Abstract
This report briefly presents the arguments of De Masi-Ferrari-Golstein-Wick and Kipnis-Varadhan to derive an (annealed) invariance principle for the random walk in a random environment.
Type
Publication
Oberwolfach Report of the Arbeitsgemeinschaft: Quantitative Stochastic Homogenization
This report was written as a detailed abstract for the presentation I gave during the Arbeitsgemeinschaft: Quantitative Stochastic Homogenization, organized by A. Gloria and F. Otto in Oberwolfach in October 2022.
The picture above illustrates a key point in the proof of De Masi-Ferrari-Golstein-Wick and Kipnis-Varadhan: one should rather look at the environment as seen by the particle (thus the environment is itself a process changing with time) to derive invariance principles. For a particle starting from the center of the square at time 0, the left-hand-side image shows the position at time 1, while the right-hand-side image shows the environment seen by the particle at time 1, which is just the l.h.s. grid appropriately shifted.