M2 - Images

TP1 - transformations et pipeline

Partie 1 : affichage d'une primitive.

L'opération fondamentale réalisée par un pipeline de rendu est le dessin d'une primitive : déterminer quels pixels permettent de remplir une forme "simple" dans l'image résultat.

Cette opération est découpée en plusieurs étapes :

transformation des sommets de la primitive dans le repère projectif homogène de la camera,
identifier les pixels qui font partie de la forme,
colorier les pixels.

exercice 1 : transformations

    Les objets et leurs sommets sont décrits dans un repère local, puis ces objets sont placés et orientés dans le repère de la scène. Un observateur / camera est également placé et orienté dans le repère de la scène. Une transformation de projection 3d vers 2d est aussi associée à l'observateur. Ces 3 transformations sont classiquement représentées par des matrices homogenes 4x4 :
    Model (transformation du repère local au repère de la scène),
    View (transformation du repère de la scène au repère camera)
    Projection (transformation du repère camera au repère projectif homogène de la camera).

Plus une autre qui représente les dimensions de l'image résultat :
    Viewport (transformation du repère projectif homogène vers le repère de l'image).

Il est possible de composer ces matrices afin de construire une seule matrice de transformation permettant de passer directement du repère local de l'objet au repère de l'image. Ecrivez cette relation.

Par construction de la transformation de projection, les points visibles par l'observateur se retrouvent dans le repere projectif (apres transformation) à l'interieur du cube unitaire [-1 1] sur les 3 axes.

Si l'on choisit une matrice identité comme projection, ou peut on placer des points qui seront visibles / associés à un pixel de l'image ?

prise en main de gKit :

mise à jour : 09/10/2014

version de gKit2 et des dépendances precompilées pour les salles tp7 et tp8 du nautibus.
premake4 est également disponible dans ./local/linux32/bin/premake4

pour construire les makefiles pour compiler le tp :

    ./local/linux32/bin/premake4 gmake
    make tp1 -j4
    ./tp1

mise à jour : 24/09/2013

version de gKit2 et dépendances precompilées pour les salles tp du nautibus.
premake4 est également disponible dans ./local/linux/bin/premake4

pour construire les makefiles pour compiler le tp :

    ./local/linux/bin/premake4 gmake
    make -j4
    ./main

mise à jour des infos pour recompiler les dépendances sur mac et linux sur la page précédente.

installez gKit et ses dépendances.
compilez la doc avec Doxygen. Elle sera consultable dans doc/html/index.html. Les classes de bases sont documentées dans la partie module de la documentation générée.

gKit utilise la classe gk::Transform pour représenter et manipuler les transformations. Les classes gk::Point et gk::Vector permettent de représenter un point et un vecteur. Les fonctions de construction des transformations standards sont aussi disponibles : gk::Translate(), gk::Rotate(), gk::Perspective().

La transformation d'un point s'écrit directement :

    gk::Transform T;     
      // identité

gk::Point p;

    gk::Point q= T(p);   
      // renvoie le point reel transforme

La composition de transformations est aussi disponible :
gk::Transform A, B;

gk::Transform C= A * B;

La transformation inverse est également calculée :
gk::Transform M= C.inverse();

Pour obtenir le point homogène après la transformation d'un point p :
gk::HPoint h;

    M(p, h);    //
      renvoie le point homogene apres la transformation

Si le point homogène est dans la zone visible (le cube unitaire -1, 1), on peut le projetter / normaliser pour obtenir le point 3d associé :
gk::Point q;

if(h.isVisible())

q=
      h.project();    // projette le point homogene dans
      l'espace 3d reel.

gKit utilise la classe gk::Image pour représenter un ensemble de pixels et fournit egalement des fonctions permettant d'enregistrer l'image dans un fichier.
gk::Image *image= new gk::Image(largeur, hauteur);

gk::ImageIO::writeImage("resultat.bmp", image);

Les méthodes gk::Image::pixel(x, y) et gk::Image::setPixel(x, y, color) permettent de lire et de modifier la couleur du pixel de coordonnées x, y. La classe de base gk::VecColor représente une couleur par un triplet rouge, vert, bleu, avec des valeurs comprises entre 0 et 1.

exemple:

#include "Vec.h"      // type
      vecteur, point, couleur, etc. de "base"

#include "Image.h" // classe image

#include "ImageIO.h"  // entrees / sorties sur des
      images

int main( )

{

    gk::Image *image=
      gk::createImage(512, 512)

;

   




      // cree une image de 512x512 pixels

    // parcourir tous les pixels de
      l'image

    for(int y= 0; y <
      image->height; y++)

    // chaque
      ligne

        for(int x= 0; x
      < image->width; x++)    // chaque colonne

           
      image->setPixel(

x, y, gk::VecColor(1, 0, 0));

   














      // colorie chaque pixel en rouge

// enregistre le resultat

    gk::ImageIO::writeImage("out.bmp",
      image);



          

          delete image;

          return 0;

}

exercice 2 : version fragmentation / rasterization.

Choisissez 3 sommets p0, p1, et p2 ainsi que leur transformation dans le repère image après projection et vérification de leur visibilité (on suppose que les 3 sommets sont visibles et se projettent sur l'image).

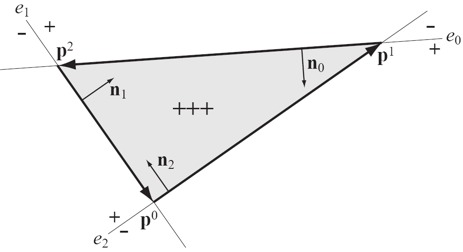
Définissez les équations 2d des 3 arêtes du triangle e0, e1, e2, sous la forme : e(x,y)= ax + by + c.

Un pixel (px, py) est à l'intérieur du triangle s'il se trouve dans le demi plan positif défini par chaque arête (du coté de la normale),
c'est dire si e0(px, py) > 0, e1(px, py) > 0 et e2(px, py) > 0.

Comment construire les équations des arêtes pour vérifier cette condition ?
indication :
    l'aire signée d'un triangle orienté dans le plan se calcule directement : cf Modern triangles / section Modern triangles
    aire signée du triangle p0, p1, p2= 0.5 * [ (x1 - x0) * (y2 - y0) - (x2 - x0) (y1 - y0) ]

    on peut également calculer l'aire signée du triangle formé par l'arete p0p1 et un point p : aire p0p1p = 0.5 * [ (x1 - x0) * (py - y0) - (px - x0) (y1 - y0) ]
    et le reformuler : e0(px, py)= a0*px + b0*py + c0= [-(y1 - y0)] * px + [(x1 - x0)] * py + [x0 * (y1 - y0) - y0 * (x1 - x0)]

première solution :
    déterminez le rectangle englobant les 3 sommets dans le repère image et testez l'inclusion de tous les pixels de ce rectangle.

solution efficace ?
Proposez une solution qui teste des blocs de pixels dans un premier temps, puis qui teste tous les pixels des blocs couvrant (partiellement ou entièrement) le triangle.

Comment déterminer efficacement qu'un bloc se trouve entièrement à l'extérieur du triangle (sans tester tous les pixels) ?
(indication : ses 4 sommets sont à l'exterieur de la même arête du triangle)

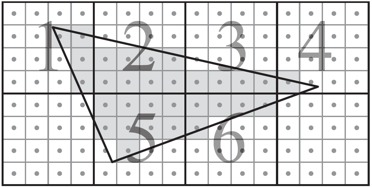
Lorsqu'un bloc contient, au moins partiellement, le triangle, testez tous les pixels du bloc (les blocs 1 à 6 dans l'exemple).

Cette "optimisation" est-elle interressante dans tous les cas ? Comment choisir la taille des blocs ?

pour les curieux :
Que se passe-t-il lorsque un ou plusieurs sommets ne sont pas visibles ? Il n'est plus possible de faire le test en 2d dans le plan image, il faut transposer les tests dans le repère projectif homogène 4d. Une solution élégante est présentée section 2 dans :
"Incremental and Hierarchical Hilbert Order Edge Equation Polygon Rasterization"
M.D. McCool, C. Wales, K. Moule,
gh 2001

exercice 3 : version Reyes, subdivision.

Une autre solution, applique directement le principe "diviser pour règner" au problème. Il est immédiat de dessiner un objet plus petit qu'un pixel, dans les autres cas, il suffit de découper l'objet.

Proposez une solution utilisant cette idée.
indication : pour subdiviser un triangle en 4, il suffit de calculer le point milieu de chaque arête et de construire les 4 sous triangles.

Cette solution peut-elle fonctionner lorsque certains sommets sont en dehors de la zone visible ? Modifiez votre programme pour inclure cette fonctionnalité.
indication : il serait judicieux d'arreter la subdivision lorsque une partie de la surface est entierement non visible.

exercice 4 : version lancer de rayon.

La dernière catégorie de solution consiste à déterminer l'équation de la droite passant par le centre de chaque pixel de l'image et à tester l'intersection de cette droite avec le triangle.
La classe gk::Triangle fournit le test d'intersection d'un triangle et d'un rayon, cf gk::Triangle::intersect(). En résumé, la fonction calcule l'intersection de la droite avec le plan portant le triangle puis vérifie que le point est bien à l'intérieur du triangle.

Comment calculer les extrémites du rayon passant par le centre du pixel (x, y) ? Dans quel espace est-il le plus simple de travailler ?

indication : la classe gk::Ray représente un rayon par son origine, o, et sa direction, d. Un point le long du rayon est represente p(t)= o + t . d

Partie 2 : affichage d'une surface.

Mêmes questions avec une surface simple : une sphère de rayon R et de centre c. Il existe de nombreuses manières de représenter une sphère, dans chaque cas il faut choisir la version la plus adaptée.

indications pour la version lancer de rayon.
La dérivation du test d'intersection entre une droite et une sphère se trouve sur wikipedia, par exemple :
http://en.wikipedia.org/wiki/Line%E2%80%93sphere_intersection

Dans ce cas, on utilise la forme implicite f(x, y, z) = 0 indiquant les points à la surface de la sphère.

indications pour la version Reyes.
Il faut choisir une représentation de la surface qui permette de manipuler une partie de la surface.
La représentation paramétrique semble bien adaptée, la surface complète est décrite par 2 angles, theta variant entre 0 et pi (angle par rapport à l'axe Y) et phi variant entre 0 et 2pi (angle par rapport à l'axe X). Une partie de la surface sera representée par un intervalle sur theta et un autre sur phi. Pour subdiviser la surface, il suffit de couper chaque intervalle en deux pour obtenir 4 sous surfaces.

Le découpage de la partie de la surface va changer le comportement de l'algorithme : un découpage régulier de l'intervalle \theta, \phi ne crée pas un découpage régulier de la surface de la spĥère (pourquoi ?). Peut-on découper la surface de la sphère de manière régulière ? Quel avantage peut on attendre d'un découpage régulier ?

indications pour la version raster.
Il faudrait convertir la surface de la sphère en un ensemble de triangles et ensuite les dessiner.

Réalisez la version lancer de rayon et reyes.

Partie 3 : affichage d'une surface perturbée.

Mêmes questions pour une sphère dont le rayon est perturbé : le rayon devient une fonction de la position à la surface de la sphère.
Une sphère de centre 0 et de rayon R peut être représentée, sous forme implcite, par : x² + y² + z² - R² = 0,
et une sphère perturbée par : x² + y² + z² - (R + f(x, y, z))² = 0.

indications pour la version lancer de rayons.
Selon la forme de f, la fonction de perturbation, il peut être compliqué de trouver explicitement les intersections avec le rayon.
Dans ce cas, il possible d'utiliser une recherche en évaluant l'équation de la sphère perturbée en plusieurs points le long du rayon. Selon la position sur le rayon le résultat sera soit négatif soit positif, l'idée est d'identifier un (petit) intervalle de positions sur le rayon qui encadre la "vraie" intersection avec la surface.

Cette technique permet de faire de choses assez impressionnantes, avec un peu de puissance de calcul :
les bases de cette manière de décrire des objets sont résumées et illustrées par Inigo Quilez : http://www.iquilezles.org/www/articles/distfunctions/distfunctions.htm

ainsi que d'autres exemples de construction : http://www.iquilezles.org/www/articles/menger/menger.htm

indications pour la version Reyes.
Dans ce cas, il est plus simple d'utiliser la forme paramétrique de la sphère perturbée. Une solution directe consiste à exprimer la perturbation en fonction des angles theta et phi : f(\theta, \phi) au lieu de f(x, y, z).

Réalisez la version lancer de rayons et reyes.

Pour les curieux : affichage de plusieurs surfaces et filtrage.

Modifiez une des solutions d'affichage pour traiter le cas de plusieurs triangles ou sphères pouvant se recouvrir.

Modifiez une des solutions d'affichage pour traiter le cas d'objets semi transparents.

Modifiez une des solutions d'affichage pour produire une version filtrée de l'image : la contribution d'une primitive à un pixel devrait être proportionnelle à l'aire visible de l'intersection de la primitive et du pixel.

Modifiez la version Reyes pour la rendre plus efficace. Il est couteux de subdiviser récursivement chaque surface jusqu'a obtenir une projection inférieure à un pixel. Réalisez l'opération dice du pipeline Reyes (c'est la même idée que le test par bloc de pixels utilisé par la rasterization.) L'objectif est produire une grille régulière à la surface de l'objet dont chaque cellule se projette approximativement sur un pixel.