on vient de voir qu'estimer une intégrale avec Monte Carlo et les proba fonctionne plutot bien mais que selon le nombre d'échantillons utilisé des erreurs assez importantes peuvent être visibles dans l'image, cf Monte Carlo et équation de rendu. on a également constaté que la densité de proba utilisée pouvait avoir une influence importante sur ces erreurs, cf Monte Carlo et éclairage direct.

comment choisir les bons paramètres ? le nombre d'échantillons et leur densité de proba ?

vu que tout ça est basé sur des proba, et que l'on construit une variable aléatoire pour estimer l'intégrale, on peut se rendre compte que l'estimateur lui même est aussi une variable aléatoire (!!) et que l'on peut estimer plusieurs choses : son espérance, bien sur, on vient de la calculer, mais aussi sa variance et son erreur par rapport à une référence.

voila les définitions, pour une variable aléatoire \( x \), de densité de proba \( p(x) \). on commence par l'espérance de \( x \) que l'on a déjà utilisé :

\[ \mu= E[x] = \int x \, p(x) \, dx \approx \frac{1}{N} \sum_i^N x_i \mbox{ avec } x_i \sim p \]

et sa variance, que l'on peut définir à partir de l'espérance :

\[ \sigma^2= V[x] = E[(x - \mu)^2] \]

la variance décrit le fait que les valeurs de la variable aléatoire sont concentrées, ou pas, autour de son espérance (de sa moyenne...). une variance nulle indique que la variable aléatoire est constante.

mais ces définitions ne nous aident pas trop pour connaitre l'erreur ou la variance d'un estimateur construit avec \( N \) échantillons. il suffit de se rappeler qu'un estimateur est la valeur moyenne de \( N \) réalisations de la même variable aléatoire :

\[ I_N= \frac{1}{N} \sum_i^N x_i \]

que l'on peut aussi écrire :

\[ I_N= \frac{1}{N} \sum_i^N I_1 \]

la variance à plusieurs propriétés que l'on peut utiliser pour simplifier les calculs, on va utiliser celles-ci :

\[ \begin{eqnarray*} V[ax]&= &a^2 V[x] \\ V \left[ \sum_i^N y_i \right]&= & \sum_i^N V[y_i] \mbox{ si les N variables aléatoires } y_i \mbox{ sont indépendantes...} \end{eqnarray*} \]

on peut maintenant écrire la variance de l'estimateur \( I_N \) :

\[ V[I_N]= V \left[ \frac{1}{N} \sum_i^N I_1 \right]= \frac{1}{N^2} V \left[\sum_i^N I_1 \right]= \frac{1}{N^2} \sum_i^N V[I_1]= \frac{1}{N^2} N V[I_1] \]

et on obtient enfin un résultat utilisable :

\[ V[I_N]= \frac{V[x]}{N} \mbox{ ou } V[I_N]= \frac{\sigma^2}{N} \]

et alors ? ben maintenant, on est à peu près sur que la variance de l'estimateur décroit vers 0 lorsque le nombre d'échantillons croit vers l'infini, on a déjà constaté ce comportement dans tous les exemples d'intégration numérique, on peut même prédire à quelle vitesse la variance décroit.

ah ? mais la densité de proba à aussi une influence non ? oui, bien sur, il suffit de réécrire tout ça pour une fonction d'une variable aléatoire \( x \) :

\[ V[I_N]= \frac{1}{N} V \left[ \frac{f(x)}{p(x)} \right] \]

\( f \) est fixé, on ne peut pas vraiment la modifier, c'est la lumière qui se propage dans la scène, par contre, si on change \( p \), on doit pouvoir observer une différence... par exemple, si \( p \) est exactement proportionnelle à \( f \), ie \( p(x)= c f(x)\) avec une constante quelconque, on arrive à un résultat un peu bizarre :

\[ V[I_N]= \frac{1}{N} V \left[ \frac{f(x)}{cf(x)} \right]= \frac{1}{N} V[1/c] \equiv 0 \]

ce qui veut dire qu'en théorie, on peut calculer le résultat exact avec un seul échantillon !! oui, mais en pratique, si on savait déja intégrer la fonction, on ne s'embeterait pas à utiliser Monte Carlo, donc il y a quand même assez peu de chances que ce résultat soit applicable directement.

par contre, ce simple exercice montre que certaines densités de proba sont plus adaptées que d'autres, et on a déjà constaté ce comportement : dans le premier exemple d'intégration de \( \cos \) avec une densite constante et une densite décroissante, cf intégration numérique et Monte Carlo. mais également sur l'intégration de l'éclairage direct avec plusieurs sources de lumière, cf Monte Carlo et éclairage direct.

réduction de variance

au final pour réduire la variance de l'estimateur, on a 2 options :

soit faire plus de calculs, en augmentant \( N \),
soit modifier la densité de proba pour générer les échantillons (les points sur les sources ou les directions) en espérant trouver une solution plus intérressante, mais il n'y a pas de solutions magique qui permet de déterminer, a priori, quelle est la meilleure solution...

ie pour réduire la variance par 2, on peut soit faire 2 fois plus de calculs, soit trouver une densité de proba telle que la variance de l'estimateur soit 2 fois plus petite...

on peut bien sur simplement calculer des series d'images avec des densités de proba différentes et garder la meilleure, mais on a quand même un indice sur une 'bonne' densité de proba, elle doit être, au moins à peu près, proportionnelle à la fonction intégrée... et c'est bien ce que l'on avait observé dans intégration numérique et Monte Carlo en intégrant \( \cos \) avec une densité de proba décroissante, ie qui varie à peu près de la même manière que \( \cos \), revoila quelques réalisations des 2 estimateurs : avec une densité de proba constante ou pas :

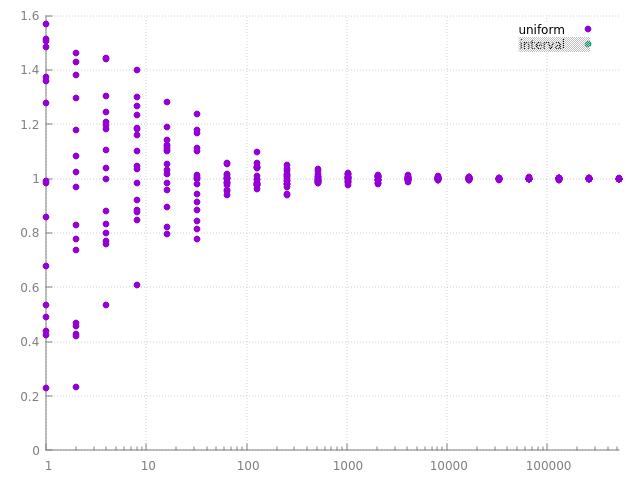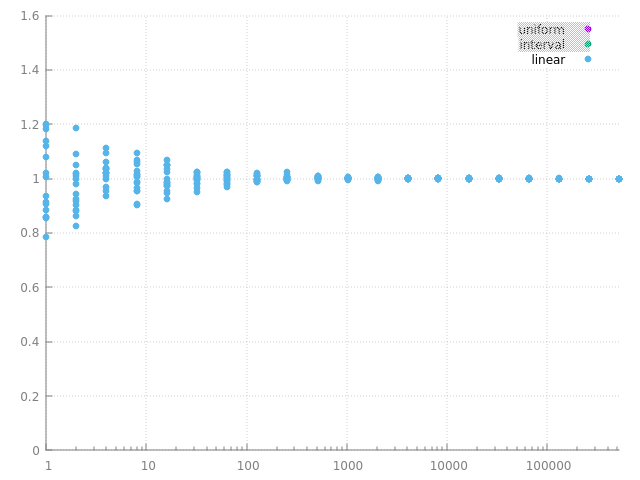plus la variance est faible, plus les réalisations de l'estimateur sont concentrées / regroupées autour de l'espérance, c'est bien ce que l'on observe... et pour un même nombre de calculs, ou d'échantillons, on observe bien que l'estimateur de droite à une plus petite variance que celui de gauche.

remarque : souvent on estime l'erreur moyenne, notée RMSE et pas la variance \( \sigma^2 \). pourquoi ? la variance n'a pas la même unité que la valeur estimée, à cause du carré. l'erreur moyenne de l'estimateur s'écrit

\[ \mbox{RMSE}= \frac{\sigma}{\sqrt N} \]

pour avoir une erreur 2 fois plus petite, il faut faire 4 fois plus de calculs, à cause de \( \sqrt N \).

variance en image...

vu que la variance est définie en fonction de l'espérance, on peut aussi l'estimer, à peu près de la même manière que la couleur du pixel. on peut utiliser cette relation pour faire le calcul :

\[ V[x]= E[(x - \mu)^2]= E[x^2] - \mu^2= E[x^2] - E[x]^2 \]

voila un exemple sur la cornell box en choisissant des point sur les sources :

remarque : utiliser directement cette définition n'est pas très stable numériquement, à cause de la précision limitée des floats, cf wikipedia pour une solution numérique correcte.

on constate bien que lorsque la variance est importante, en blanc sur l'image du dessus, l'estimateur produit des défauts qui s'estompent en augmentant le nombre de calculs par pixel, à gauche N= 4 et à droite N= 16. par exemple, le bruit sur les murs est beaucoup moins visible avec 16 échantillons qu'avec 4. les pénombres des cubes sont un peu mieux avec 16 échantillons, mais le bruit est toujours bien visible. il faudra faire plus de calcul pour obtenir une estimation précise dans ces parties de l'image (ou filtrer avec un plus gros support...)

remarque : oui, faire 4 fois plus de calculs permet de diminuer visiblement l'erreur moyenne RMSE de l'estimateur. mais c'est aussi 4 fois plus long...

autre détail interressant, les zones de l'image les plus difficiles à intégrer, avec une variance importante, sont soit dans les 'reflets' sur les murs, soit dans les pénombres, mais également sur la face supérieure du grand cube, ie quand un objet est proche de la source de lumière qui l'éclaire.

sur l'autre scène avec les 2 gros panneaux lumineux, cf Monte Carlo et éclairage direct, on peut même regarder les différences entre 2 stratégies :

soit choisir des directions aléatoires et espérer toucher une source de lumière, cf colonne de gauche,
soit choisir un point sur une source en fonction de l'aire de la source, cf colonne de droite

d'abord les rendus avec N = 256 :

et les variances des 2 estimateurs : à gauche choisir une direction, à droite choisir une source en fonction de son aire :

le résultat est quand même bien différent ! choisir un point sur les sources produit une variance vraiment plus petite !! sauf juste devant les panneaux lumineux ou choisir une direction est mieux... mais partout ailleurs, choisir une source a une variance vraiment plus faible. c'est le même constat qu'au dessus, dans la cornell box, les objets proches des sources ont une variance importante, lorsque l'on choisit une source puis un point sur cette source.

et alors ?

on vient de voir que la variance des estimateurs est bien liée à la fonction intégrée et à la densité de proba utilisée. soit les pénombres, ie le terme \( V(p, q) \), soit la distance entre p et q, ie le terme \( 1 / || \vec{pq} ||^2\) introduisent de la variance dans l'estimateur... le choix de la source de lumière à aussi l'air d'avoir une influence, comme observé dans Monte Carlo et éclairage direct.

comment choisir a priori une densité de proba correcte ?

il n'y a pas de solution magique, mais on peut quand même analyser les différents termes de l'équation de rendu et proposer, dans chaque cas, une densité de proba correcte.

par exemple, lorsque l'on intègre l'éclairage ambiant, comme dans l'exemple de Monte Carlo, éclairage direct : structurer le code :

\[ L_r(p, \vec{o}) = \int_{\Omega} \frac{k}{\pi} V(p, \vec{l}) \cos \theta \, dl \]

on intègre le produit de 2 fonctions, la visibilité du ciel, \( V(p, \vec{l}) \) et le \( \cos \theta \). on ne connait pas la visibilité, par contre, on peut sans doute faire quelquechose avec le \( \cos \)... on a déjà vu qu'une densité de proba linéaire est mieux qu'une densité uniforme, dans ce cas...

peut-on directement utiliser \( \cos \) comme densité de proba ? ou de manère générale : peut-on utiliser une fonction comme densité de proba ? oui, mais à certaines conditions :

une densite de proba est normalisée : \( \int p(x) \, dx = 1\),
la densité de proba ne doit pas être nulle si la fonction intégrée n'est pas nulle, ie il faut pouvoir évaluer \( \frac{f(x)}{p(x)}\), et placer des échantillons partout où la fonction n'est pas nulle,
on doit pouvoir calculer la fonction de répartition : \( P(x)= \int_0^x p(t) \, dt \),
et pour générer des échantillons selon la densité de proba à partir d'un (ou plusieurs) nombre aléatoire, u, uniforme entre 0 et 1, il faut pouvoir inverser la fonction de répartition, \( x= P^{-1}(u)\)...

oui, ça fait pas mal de contraites sur les fonctions que l'on va pouvoir utiliser...

mais pour \( \cos \), voila le résultat :

\[ \begin{eqnarray*} p(\vec{l})&= & \frac{\cos \theta}{\pi}\\ \cos \theta &= & \sqrt{u_1}\\ \phi &= & 2\pi \, u_2\\ \vec{l} &= & ( \cos \phi \sin \theta, \, \sin \phi \sin \theta, \, \cos \theta)\\ \mbox{avec }\sin \theta &= & \sqrt{1 - \cos \theta \cos \theta} \end{eqnarray*} \]

sans surprise, \( p(\vec{l}) \), la densité de proba, est proportionnelle à \( \cos \). ce qui signifie que si on intégrait uniquement \( \cos \) le résultat serait exact avec 1 échantillon... mais bien sur on intègre le produit du cos et de la visibilité... la variance sera a priori très très faible dans les zones qui voient entièrement le ciel et plus importante sur les 'pénombres' :

voila les variances des 2 estimateurs, à gauche, une densité uniforme \( 1 / 2\pi\), et à droite, la nouvelle \( \cos / \pi \):

la variance est au minimum divisée par 2, sur le sol entre les cubes, par exemple, et à peu près par 10 en s'éloignant des cubes... pas mal pour une modification d'une seule ligne dans le code (bon ok, 2 lignes)...

une dernière remarque, sur la face supérieure du grand cube, la variance est quasi nulle : en effet, la visibilite du ciel est parfaite et la fonction V devient une constante qui n'introduit pas de variance.

autre exemple, l'éclairage direct avec les 2 panneaux lumineux en choisissant des directions. voila les variances de 2 estimateurs : à gauche, une densité uniforme \( 1 / 2\pi\), et à droite, \( \cos / \pi \):

c'est mieux aussi dans ce cas ! au pied du panneau de droite dans l'image, la variance passe 0.25 à 0.15, pas tout à fait la moitiée, mais c'est mieux. donc, utiliser la densité proportionnelle à cos, à l'air d'être une vraie bonne idée dans tous les cas (éclairage ambiant ou direct)...

pour les malins : vous pouvez aussi constater qu'utiliser une densité avec un cos permet de simplifier l'écriture de l'estimateur, et comme on intégre une fonction de moins, ie avec des variations en moins... l'estimateur converge mieux. par exemple celui-la :

\[ \require{cancel} \begin{eqnarray*} L_r(p, \vec{o}) &= & \frac{1}{N} \sum_i^N \frac{k}{\pi} V(p, \vec{l_i}) \cos \theta_i \, \frac{1}{p(\vec{l_i})}\\ &= & \frac{1}{N} \sum_i^N \frac{k}{\cancel{\pi}} V(p, \vec{l_i}) \cancel{\cos \theta_i} \, \frac{1}{\frac{\cancel{\cos \theta_i}}{\cancel{\pi}}}\\ &= & \frac{1}{N} \sum_i^N k V(p, \vec{l_i}) \mbox{ avec } \vec{l_i} \sim \frac{\cos \theta_i}{\pi} \end{eqnarray*} \]

résumé

réduire la variance d'un estimateur Monte Carlo en choisissant une densité de proba adaptée, ie approximativement proportionnelle à la fonction integrée, permet de réduire les variations de \( \frac{f}{p}\), ie la variance de l'estimateur en plaçant plus d'échantillons dans les régions du domaine d'intégration ou la fonction a des valeurs importantes. ces techniques portent un nom : échantillonnage préférentiel ou importance sampling.

on vient de voir sur un exemple simple que c'est finalement assez efficace quand un seul terme introduit beaucoup de variance dans l'estimateur, mais c'est quand même dommage de ne pas pouvoir s'adapter à la fonction intégrée : on a également vu, dans la scène éclairée par les 2 panneaux lumineux que la meilleure solution dépend de la situation, ie proche ou loin d'un panneau... on aimerait aussi pouvoir choisir la meilleure densité de proba ou, peut être, les mélanger pour pouvoir réduire la variance et l'erreur dans toutes les situations...

on peut essayer de faire la moyenne des 2 stratégies (choisir une direction ou choisir un point sur une source), mais on sait à l'avance que ca ne permettra pas de réduire de la variance : les variances de 2 variables aléatoires s'additionnent, ie le résultat sera toujours moins bon...

mais bien sur, il y a une solution !! la suite dans Monte Carlo et MIS...