jusqu'à présent on s'est interessé à l'éclairage direct : la lumière émise par les sources de lumière qui arrive directement sur un point p de la scène, cf Monte Carlo et équation de rendu et Monte Carlo et éclairage direct. on a intégré soit sur toutes les directions de l'hemisphere autour de p, soit sur les points des sources de lumière :
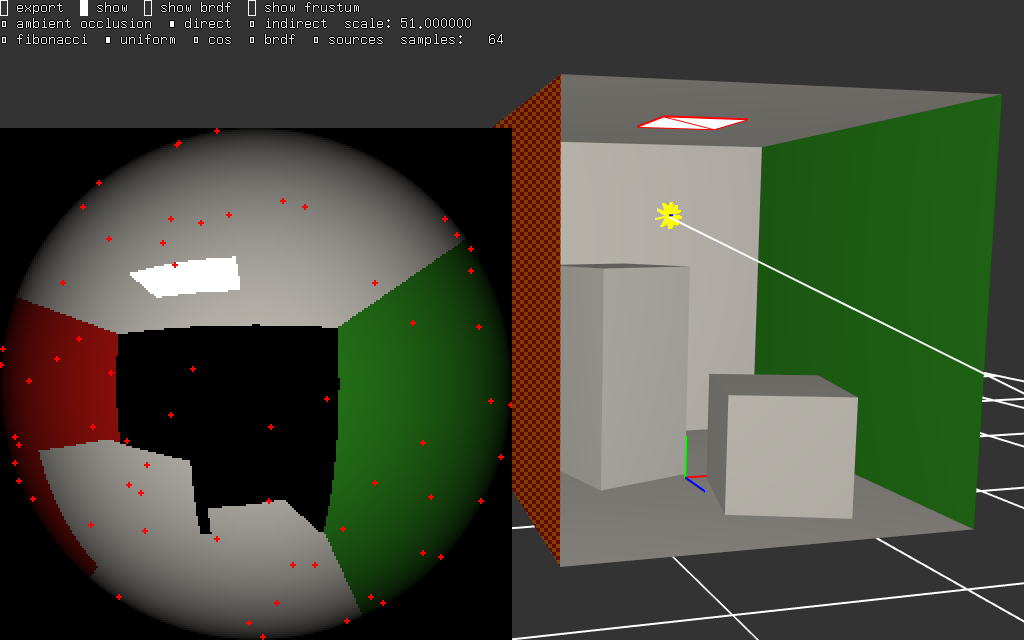 | 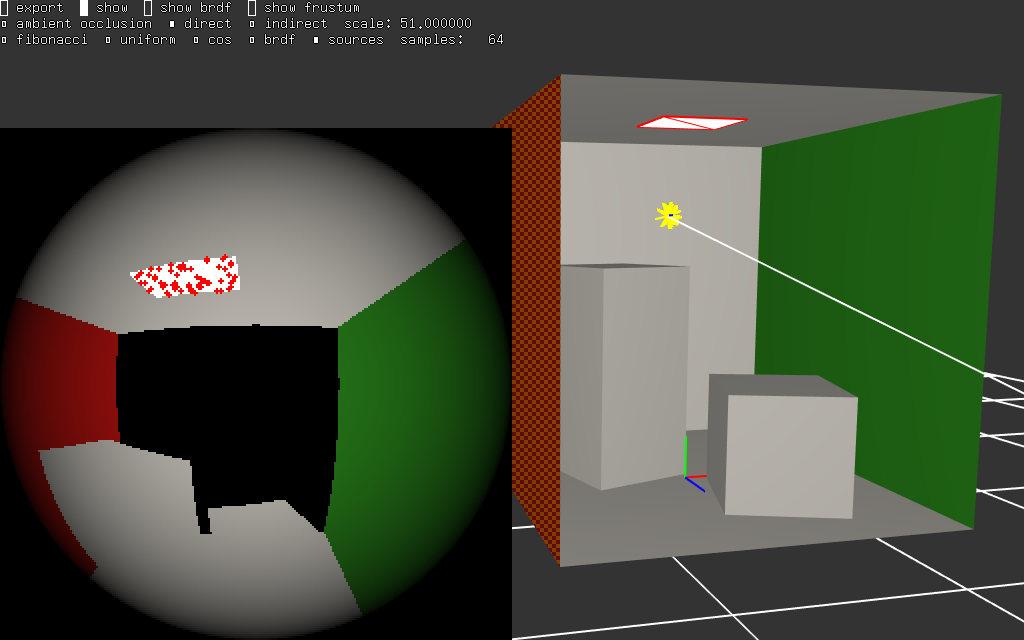 |
les sources de lumière sont en blanc dans les vignettes en bas à gauche des images. les autres pixels des vignettes indiquent la couleur des objets de la scène, ce qui permet de mieux se repérer, mais tous ces points ne contribuent pas au calcul. les points rouges montrent les échantillons utilisés pour estimer l'équation de rendu.
voila le résultat en image : ie l'éclairage direct évalué pour le point visible pour le centre de chaque pixel de l'image :

mais tous ces points, visibles par p, sont eux aussi éclairés par les sources de lumière et on peut également évaluer la lumière qu'ils réfléchissent vers p :
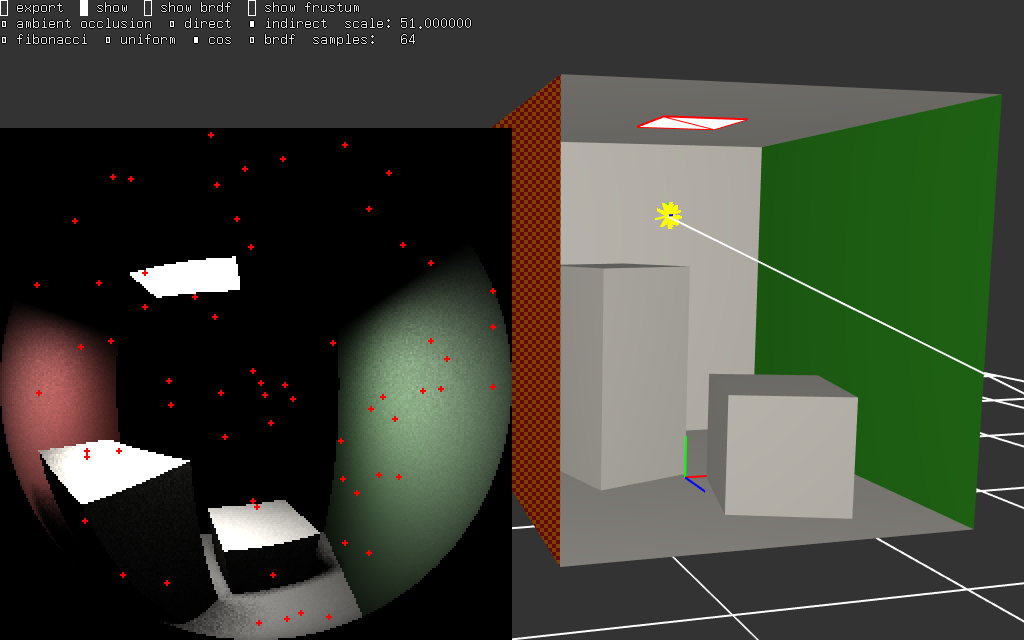
voila le résultat avec ce calcul supplémentaire, ie l'éclairage indirect :

on constate que les zones d'ombres ne sont plus toutes noires... par exemple, la face gauche du grand cube est toute rouge : le mur de gauche est éclairé par la source et une bonne partie de cette lumière se réfléchi vers le grand cube. c'est bien visible aussi sur le plafond, tous les objets éclairés par la source réfléchissent de la lumière et une partie de cette lumière éclaire le plafond.
comment formuler et calculer ça ?
pour calculer l'éclairage direct, on a utilisé l'équation de rendu : on a séparé l'ensemble de directions qui peuvent éclairer le point p en deux parties : les directions qui correspondent aux sources de lumière et les autres, qui correspondent à des objets... pour les directions qui correspondent aux sources de lumière, on connait la lumière incidente, c'est l'emission de la source, mais on a considéré que les directions qui correspondent aux objets ne contribuent pas.
on peut l'écrire comme ça :
\[ \begin{eqnarray*} L_r(p, \vec{o}) &= & L_e(p, \vec{o}) + \int_{\Omega} \frac{k_p}{\pi} V(p, \vec{l}) L_i(p, \vec{l}) \cos \theta \, dl\\ \mbox{avec } L_i(p, \vec{l}) &= & L_e(q, -\vec{l}) \neq 0 \mbox{ si q se trouve sur une source}\\ \mbox{et } q &= & \mbox{hit}(p, \vec{l}) \mbox{ un point q visible depuis p dans la direction } \vec{l} \end{eqnarray*} \]
ie on intégre l'emission des sources de lumière vues par le point p. pour les autres objets, leur matière n'emet pas de lumière et le terme \( L_e(q, -\vec{l}) \) est nul. mais ça ne signifie pas qu'aucune lumière n'est réfléchie par le point q vers le point p... par contre, il va falloir faire le calcul.
c'est exactement ce qu'exprime l'équation de rendu : on peut évaluer ce qui est réfléchi par un point en intégrant ce qui éclaire ce point : ie calculer \( L_r() \) en intégrant \( L_i() \) ! (plus précisement en intégrant \( L_i() \cdot f_r() \cdot \cos\), ne pas oublier la reflexion de la lumière par la matière...)
et dans les scènes simples, sans volume, ni brouillard, ni fumée, etc. ce qui est réfléchi par un point q dans une direction, éclaire un point p, visible dans cette direction :
\[ \begin{eqnarray*} L_i(p, \vec{l})&= & L_r(q, - \vec{l})\\ \mbox{et } q &= & \mbox{hit}(p, \vec{l}) \mbox{ un point q visible depuis p dans la direction } \vec{l} \end{eqnarray*} \]
c'est sans doute plus clair, sur un schéma :
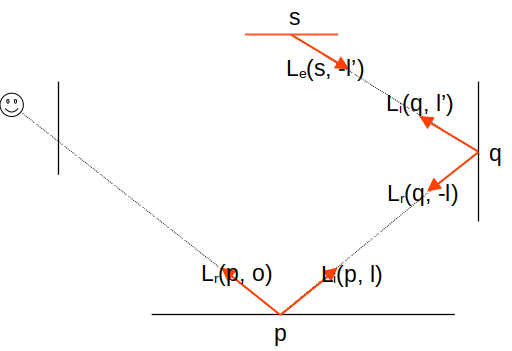
avec ces 2 propriétés, il ne reste plus qu'à écrire la substitution, ie remplacer \( L_i(p, \vec{l}) \) par \( L_r(q, -\vec{l}) \) :
\[ \begin{eqnarray*} L_r(p, \vec{o}) &= & L_e(p, \vec{o}) + \int_{\Omega} \frac{k_p}{\pi} V(p, \vec{l}) L_i(p, \vec{l}) \cos \theta \, dl\\ \mbox{avec } L_i(p, \vec{l}) &= & L_e(q, -\vec{l}) \neq 0 \mbox{ si q se trouve sur une source}\\ \mbox{ou } L_i(p, \vec{l}) &= & L_r(q, -\vec{l})= \int_{\Omega} \frac{k_q}{\pi} V(q, \vec{l'}) L_i(q, \vec{l'}) \cos \theta' \, dl' \mbox{ sinon}\\ \mbox{et } q &= & \mbox{hit}(p, \vec{l}) \mbox{ un point q visible depuis p dans la direction } \vec{l} \end{eqnarray*} \]
on peut ré-ecrire tout ça directement :
\[ \begin{eqnarray*} L_r(p, \vec{o}) &= & L_e(p, \vec{o}) + \int_{\Omega} \frac{k_p}{\pi} V(p, \vec{l}) L_i(p, \vec{l}) \cos \theta \, dl\\ \mbox{avec } L_i(p, \vec{l}) &= & L_r(q, -\vec{l})= L_e(q, -\vec{l}) + \int_{\Omega} \frac{k_q}{\pi} V(q, \vec{l'}) L_i(q, \vec{l'}) \cos \theta' \, dl'\\ \mbox{et } q &= & \mbox{hit}(p, \vec{l}) \mbox{ un point q visible depuis p dans la direction } \vec{l} \end{eqnarray*} \]
mais il manque encore la formulation de \( L_i(q, \vec{l'}) \) ! on souhaite calculer la lumière qui éclaire directement le point q, donc on substitue encore :
\[ \begin{eqnarray*} L_i(q, \vec{l'}) &= & L_e(s, -\vec{l'})\\ \mbox{et } s &= & \mbox{hit}(q, \vec{l'}) \mbox{ un point s visible depuis q dans la direction } \vec{l'} \end{eqnarray*} \]
le schema au dessus place les points p, q, et s ainsi que les directions utilisées.
c'est sans doute un peu bizarre, mais ré-écrire l'équation de rendu sous cette forme permet de se rendre compte qu'elle est récursive... puisque pour évaluer la lumière incidente en p, il faut calculer la lumière réfléchie par les points q qui peuvent éclairer p... et pour évaluer ce qui est réfléchi par un point q, on commence par calculer ce qui éclaire q, etc.
on arrive, enfin ! à l'expression complète que l'on va évaluer :
\[ \begin{eqnarray*} L_r(p, \vec{o}) &= & L_e(p, \vec{o}) + \int_{\Omega} \frac{k_p}{\pi} V(p, \vec{l}) L_i(p, \vec{l}) \cos \theta \, dl\\ \mbox{avec } L_i(p, \vec{l}) &= & L_e(q, -\vec{l}) + \int_{\Omega} \frac{k_q}{\pi} V(q, \vec{l'}) L_e(s, -\vec{l'}) \cos \theta' \, dl'\\ \mbox{et } q &= & \mbox{hit}(p, \vec{l}) \mbox{ un point q visible depuis p dans la direction } \vec{l}\\ \mbox{et } s &= & \mbox{hit}(q, \vec{l'}) \mbox{ un point s visible depuis q dans la direction } \vec{l'} \end{eqnarray*} \]
1 rebond
on a maintenant tous les ingrédients pour finir le calcul... on commence par générer une direction \( \vec{l} \), on calcule les intersections avec les objets de la scène pour trouver le point q, et en fonction de la matière de q, on évalue l'éclairage direct de q ou pas... mais pour évaluer l'éclairage direct de q, on recommence : on génère une direction \( \vec{l'} \) pour trouver un point \( s \) sur une source de lumière. oui, il y a bien 2 intégrales à calculer...
avant de se lancer dans les calculs, il faut peut être se poser une question supplémentaire : combien de directions \( \{ \vec{l_i} \} \) et combien de directions \( \{ \vec{l{_i}'} \} \) ?
\( N \) pour chaque intégrale ? c'est à dire \( N^2 \) au total... si on choisit une valeur raisonnable, N= 256, par exemple, on va faire 256x256= 65536 calculs par pixel et ça va être vraiment très long... on peut bien sur faire quelques tests pour déterminer des valeurs raisonnables pour le nombre de directions et le nombre de points...
on peut aussi se rappeler qu'un seul échantillon Monte Carlo est un estimateur correct d'une intégrale, mais avec une variance N fois plus importante... cf l'analyse de la variance dans Monte Carlo, convergence et réduction de variance.
et alors ? ben la solution raisonnable est d'utiliser N directions \( \{ \vec{l_j} \} \) mais 1 seule direction \( \vec{l'_0} \) pour chaque direction \( \vec{l_j} \) !! on est même sur que l'estimateur convergera vers le bon résultat en fonction de N. et que le temps de calcul de l'image sera linéaire en fonction de N...
il ne reste plus qu'à écrire l'estimateur :
\[ \begin{eqnarray*} L_r(p, \vec{o}) &= & L_e(p, \vec{o}) + \frac{1}{N}\sum_j^N \frac{k_p}{\pi} V(p, \vec{l_j}) L_i(p, \vec{l_j}) \cos \theta_j \, \frac{1}{p(\vec{l_j})}\\ \mbox{avec } L_i(p, \vec{l_j}) &= & L_e(q_j, -\vec{l_j}) + \frac{k_q}{\pi} V(q_j, \vec{l'_0}) L_e(s_0, -\vec{l'_0}) \cos \theta'_0 \, \frac{1}{p(\vec{l'_0})}\\ \mbox{et } q_j &= & \mbox{hit}(p, \vec{l_j}) \mbox{ un point q visible depuis p dans la direction } \vec{l}\\ \mbox{et } s_0 &= & \mbox{hit}(q_j, \vec{l'_0}) \mbox{ un point s visible depuis q dans la direction } \vec{l'} \end{eqnarray*} \]
remarque : il y a bien une direction \( \vec{l'_0} \) et un point \( s_0 \) différent pour chaque \( j \) (pour chaque point q), il faudrait utiliser 2 indices pour l'écrire correctement : \( \vec{l'_{j0}} \), et \( s_{j0} \) mais les notations sont déjà assez chargées comme ça...
mais en écrivant l'intégration / l'estimateur de cette manière, sur l'ensemble de directions autour de p, et des points q, le calcul de l'éclairage direct est implicite, ie on ne vise pas directement les sources de lumières qui éclairent les points p et q, et le résultat va être décevant, cf Monte Carlo et équation de rendu...
voila néanmoins quelques résultats pour N= 1, 4, 16, 64
 |  |
 |  |
argh !! comme prévu le résultat n'est pas très intéressant, même si les images sont correctes et que l'estimateur finira par converger... par exemple avec N= 1024, 4096, mais le temps de calcul n'est pas très raisonnable...
 |  |
bon on fait quoi alors ? la même chose que dans Monte Carlo et équation de rendu, on estime l'éclairage direct de manière explicite, ie en plaçant directement les points sur les sources de lumière, au lieu d'espérer les trouver par hasard en choisissant des directions...
il faut donc re-écrire l'estimateur de l'éclairage direct en p (et en q) comme dans Monte Carlo et équation de rendu, sans oublier le reste. le plus lisible est de décomposer un peu tout ça :
\[ \begin{eqnarray*} L_r(p, \vec{o}) &= & L_e(p, \vec{o}) + \mbox{direct}(p, \vec{o}) + \mbox{indirect}(p, \vec{o})\\ \end{eqnarray*} \]
ce qui permet d'utiliser une formulation adaptée pour chaque terme : intégration sur les points s pour le direct, et intégration sur les directions pour l'indirect...
\[ \begin{eqnarray*} \mbox{direct}(x, \vec{v}) &= & \int_{S} \frac{k_x}{\pi} V(x, s) L_e(s, \vec{sx}) \cos \theta_x \frac{\cos \theta_s}{||\vec{xs}||^2} \, ds\\ \mbox{indirect}(x, \vec{v})& =& \int_{\Omega_O} \frac{k_x}{\pi} \mbox{direct}(y, \vec{l}) \cos \theta \, dl \mbox{ avec } y= \mbox{hit}(x, \vec{l})\\ \end{eqnarray*} \]
remarque : direct et indirect sont définis pour des points et des directions quelconques, par uniquement p et \( \vec{l} \), d'où l'apparition de x, y et \( \vec{v} \).
cette manière d'écrire le calcul permet aussi de faire apparaitre la relation entre indirect et direct... mais attention au domaine d'intégration : \( \Omega_O \) ne représente que les directions \( \vec{l} \) qui correspondent à des objets, pas aux sources de lumière.
on peut maintenant écrire l'estimateur complet : reste un dernier détail, quand on évalue direct(p) on veut utiliser N échantillons, par contre, lors de l'évaluation de l'indirect, on doit aussi évaluer direct(), mais avec un seul échantillon \( s_0 \), pour ne pas exploser les temps de calculs. il est sans doute plus lisible de le rendre explicite :
\[ \begin{eqnarray*} \mbox{direct}(x, \vec{v}) &= & \frac{1}{N} \sum_j^N \frac{k_x}{\pi} V(x, s_j) L_e(s_j, \vec{s_jx}) \cos \theta_x \frac{\cos \theta_{s_j}}{||\vec{xs_j}||^2} \, \frac{1}{p(s_j)}\\ \mbox{indirect}(x, \vec{v})& =& \frac{1}{N} \sum_j^N \frac{k_x}{\pi} \left[ \frac{k_{y_j}}{\pi} V(y_j, s_0) L_e(s_0, \vec{s_0 y_j}) \cos \theta_{y_j} \frac{\cos \theta_{s_0}}{||\vec{y_j s_0}||^2} \, \frac{1}{p(s_0)} \right] \cos \theta_j \frac{1}{p(\vec{l_j})}\\ \mbox{et } y_j &= & \mbox{hit}(x, \vec{l_j}) \end{eqnarray*} \]
(bon ok, c'est pas super joli... )
il ne reste plus qu'à choisir les densités de proba, comme dans Monte Carlo et éclairage direct et Monte Carlo, convergence et réduction de variance.
voila quelques résultats pour N= 1, 4, 16, 64
 |  |
 |  |
et voila ce que l'on avait obtenu avec la première version de l'estimateur, pour N= 16, 64 :
 |  |
c'est un peu mieux ? non ? même s'il a fallu cogiter un peu pour arriver à ce résultat.
en résumé on a commencé par écrire une formulation 'simple' en écrivant plusieurs substitutions du terme \( L_i(p, \vec{l}) \) dans l'équation de rendu, ce qui a permis de se rendre compte que l'équation de rendu est bien récursive. on a ensuite vu que l'on pouvait, sans surprise, écrire mécaniquement un estimateur Monte Carlo, mais que ce premier estimateur n'était pas très interessant, même s'il était correct. avec un effort supplémentaire, on a re-utilisé le travail réalisé dans Monte Carlo et éclairage direct pour réduire la variance de l'estimateur en rendant l'estimation de l'éclairage direct explicite, ce qui permet d'obtenir un estimateur de l'éclairage indirect plus précis, ie avec une variance (beaucoup) plus faible.
et le code ?
le plus simple est de respecter le découpage emission + direct + indirect et d'écrire une fonction pour chaque terme qui évalue un seul échantillon :
il ne reste plus qu'à écrire la boucle pour sommer les N échantillons...
plusieurs rebonds
il n'y a pas de bonnes raisons de ne calculer qu'un seul rebond sur un objet, la lumière se propage partout... encore une fois, pour rendre le résultat à peu près lisible, on va décomposer ce que l'on calcule en plusieurs termes. chaque terme représente la lumière après une réflexion sur 1 objet, 2 objets, etc...
on connait déjà les premiers termes, on vient de les calculer : l'émission, \( L_0 \), l'éclairage direct \( L_1 \) et le premier rebond indirect \( L_2 \). à chaque terme, on ajoute un point sur lequel se réfléchi la lumière, et une intégration bien sur. on peut écrire chaque terme de la même manière, en utilisant l'équation de rendu :
\[ \begin{eqnarray*} L_0(p_0, \vec{v})&= & L_e(p_0, \vec{v})\\ L_1(p_1, \vec{v})&= & L_e(p_1, \vec{v}) + \int_{\Omega} \frac{k_1}{\pi} L_0(x, - \vec{l}) \cos \theta \, dl \mbox{ avec } x= \mbox{hit}(p_1, \vec{l})\\ L_2(p_2, \vec{v})&= & L_e(p_2, \vec{v}) + \int_{\Omega} \frac{k_2}{\pi} L_1(x, - \vec{l}) \cos \theta \, dl \mbox{ avec } x= \mbox{hit}(p_2, \vec{l})\\ L_3(p_3, \vec{v})&= & L_e(p_3, \vec{v}) + \int_{\Omega} \frac{k_3}{\pi} L_2(x, - \vec{l}) \cos \theta \, dl \mbox{ avec } x= \mbox{hit}(p_3, \vec{l})\\ \end{eqnarray*} \]
remarque : il n'y a pas de terme \( V(p, \vec{l}) \), pourquoi ? par définition, x est le point visible dans la direction \( \vec{l} \), donc \( V(p, \vec{l}) = 1\)
mais avec cette application directe de l'équation de rendu, on a encore le même problème : l'éclairage direct de chaque terme n'est calculé qu'implicitement. pour aboutir à une formulation efficace, il faut séparer les directions \( \Omega_S \) pour lesquelles une source est visible, des autres directions \( \Omega_O \). c'est èquivalent à re-décomposer chaque terme en : emission + direct + rebond, pour les termes incluant un rebond. par exemple, pour \( L_2(p_2, \vec{v}) \) :
\[ \begin{eqnarray*} L_2(p_2, \vec{v})&= & L_e(p_2, \vec{v}) \\ \mbox{(direct) } &+ & \int_{\Omega_S} \frac{k_2}{\pi} L_e(x, - \vec{l}) \cos \theta \, dl \mbox{ avec } x= \mbox{hit}(p_2, \vec{l}) \mbox{ et }L_e(x, - \vec{l}) \neq 0\\ \mbox{(indirect) } &+ & \int_{\Omega_O} \frac{k_2}{\pi} L_1(x, - \vec{l}) \cos \theta \, dl \mbox{ avec } x= \mbox{hit}(p_2, \vec{l}) \mbox{ et }L_e(x, - \vec{l}) = 0\\ \end{eqnarray*} \]
on arrive enfin à une solution explicite, en intégrant sur l'aire des sources S, ce qui permettra de faire un calcul efficace pour l'éclairage direct de chaque terme :
\[ \begin{eqnarray*} L_2(p_2, \vec{v})&= & L_e(p_2, \vec{v}) \\ \mbox{(direct) } &+ & \int_{S} \frac{k_2}{\pi} L_e(s, \vec{s p_2}) \cos \theta \frac{\cos \theta_s}{|| \vec{p_2 s} ||^2} \, ds \mbox{ avec } L_e(s, \vec{s p_2}) \neq 0\\ \mbox{(indirect) } &+ & \int_{\Omega_O} \frac{k_2}{\pi} L_1(x, - \vec{l}) \cos \theta \, dl \mbox{ avec } x= \mbox{hit}(p_2, \vec{l}) \mbox{ et }L_e(x, - \vec{l}) = 0\\ \end{eqnarray*} \]
au final, on obtient les termes suivants :
\[ \begin{eqnarray*} L_0(p_0, \vec{v})&= & L_e(p_0, \vec{v})\\ L_1(p_1, \vec{v})&= & L_e(p_1, \vec{v}) \\ &+ & \int_{S} \frac{k_1}{\pi} L_e(s, \vec{s p_1}) \cos \theta \frac{\cos \theta_s}{|| \vec{p_1 s} ||^2} \, ds \\ L_2(p_2, \vec{v})&= & L_e(p_2, \vec{v}) \\ &+ & \int_{S} \frac{k_2}{\pi} L_e(s, \vec{s p_2}) \cos \theta \frac{\cos \theta_s}{|| \vec{p_2 s} ||^2} \, ds \\ &+ & \int_{\Omega_O} \frac{k_2}{\pi} L_1(x, - \vec{l}) \cos \theta \, dl\\ L_3(p_3, \vec{v})&= & L_e(p_3, \vec{v}) \\ &+ & \int_{S} \frac{k_3}{\pi} L_e(s, \vec{s p_3}) \cos \theta \frac{\cos \theta_s}{|| \vec{p_3 s} ||^2} \, ds \\ &+ & \int_{\Omega_O} \frac{k_3}{\pi} L_2(x, - \vec{l}) \cos \theta \, dl\\ \end{eqnarray*} \]
que l'on peut schématiser :
- pour L0, on évalue juste l'émission de la matière du point p0 (la source de lumière est représentée par la barre orange) :
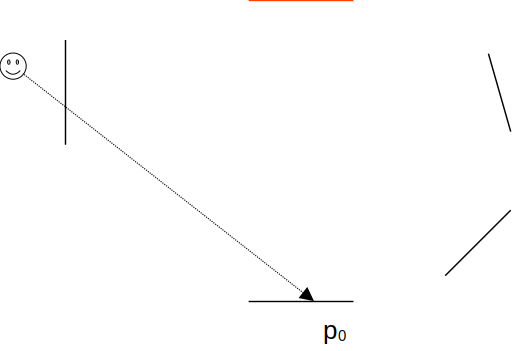
- pour L1, on intègre le direct en p1 avec N points sur les sources { s } :
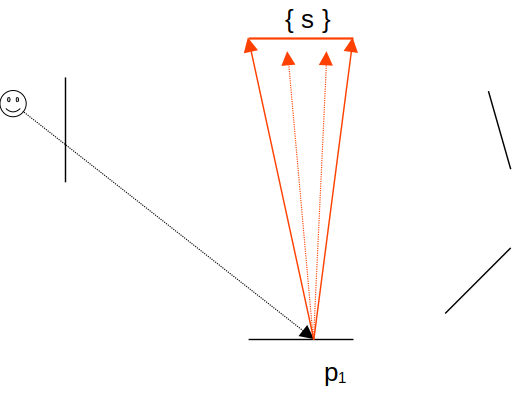
- pour L2, on intègre le direct en p2 avec N points sur les sources { s }, puis on intègre les rebonds avec N directions vers les points { p1 }, et en chaque point p1, on évalue le direct avec un seul point sur les sources :
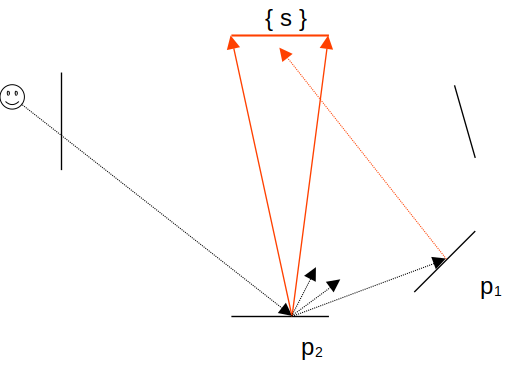
- et L3, le direct en p3 puis les rebonds avec N directions vers les points { p2 }, puis pour chaque point p2, on évalue son direct avec un point, puis on génère une direction, on trouve le point p1, on évalue son direct avec un seul point :
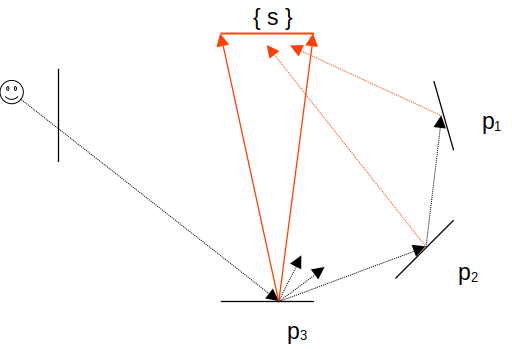
oui, c'est répétitif, ça tombe bien : on va pouvoir ré-utiliser les mêmes fonctions que tout à l'heure, direct1() et indirect1() pour estimer tout ça !!
euh ? mais pourquoi ? faut-il vraiment faire tous ces calculs ? selon où se trouvent les sources de lumières, il faut parfois simuler plusieurs rebonds pour éclairer toutes les parties de la scène. par exemple, si on décolle la source du plafond et qu'on la retourne, pour éclairer le plafond plutôt que le sol.
voici L1, l'éclairage direct (à gauche) et L2, l'éclairage indirect avec 1 rebond (à droite) pour N= 64 :
 |  |
il n'est pas très naturel d'observer une ombre parfaitement noire sur les cotés des cubes... il faut simuler au moins un rebond de plus.
voici L3, avec 2 rebonds pour N= 64 :

on peut aussi constater que l'image présente davantage de défauts : la simulation est plus complexe, et la variance est plus importante que pour simuler 1 seul rebond dans la cornell box standard lorsque la source éclaire directement presque toutes les surfaces...
bilan
on vient de construire un premier path tracer ! il reste plein de choses à améliorer, mais c'est un bon début !