Manipulations du repère courant

Remarques :

• Vous n'utiliserez pas de fonctions trigonométriques
• Le sol est le plan XY et l'arbre pousse vers le haut.
• L'objet arbre peut être paramétré par trois objets :
  • Le premier est une table de points (Racourci clavier : TNCP3)
  • le deuxième défini le graphisme du tronc.
    On suppose que le tronc à une hauteur de 1.
  • le troisième défini le graphisme de la feuille.
  En chargeant le modèle «TP/test_arbre» vous avez une ``jolie'' scène toute faite. Qui s'affichera correctement quand le TP sera terminé.
• À tous les embranchements de l'arbre, il y a le même nombre de branches.
• À chaque embranchement de l'arbre les paramètres permettant de dessiner les branches sont les même. Une branche est paramétrée par un triplet de valeurs :
  • Angle de rotation (faire pencher la branche à gauche ou à droite suivant l'axe X).
  • Facteur de rapetissement (de la branche)
  • Un angle de rotation de la branche autour de son axe (axe Z). Cet angle sera appelé angle de ``torsion''.
  Le nombre de triplets indique le nombre de branches (de sous-arbre) par embranchement.

L'arbre sera paramétré par sa profondeur de récursion :

• 0 : Une feuille
• 1 : Le tronc avec X arbres de profondeur 0 (X feuilles)
• 2 : Le tronc avec X arbres de profondeur 1 (X branches feuillus)
• ...

Si vous trouver ceci trop simple : ajouter des paramètres supplémentaires afin de choisir les différentes valeurs aléatoirement. (Voir les fonctions C rand et srand)

Dans la figure suivante (2D) l'angle ``torsion'' est nul, s'il n'est pas nul, alors la figure devient une figure 3D. De plus, il y a deux branches (X=2) au bout de chaque tronc. Et la profondeur de récursion est de neuf (N=9). Il n'y a pas de feuille.

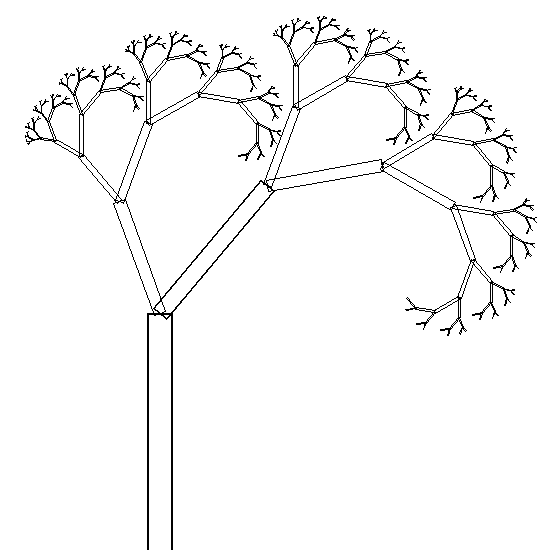
L'image précédente à été faite par le programme PostScript suivant :

/tronc {
  newpath
  -5 0   moveto
  -5 100 lineto
   5 100 lineto
   5 0   lineto
   0 0   lineto
  closepath
  stroke
} def     % Définition de la fonction affichant le tronc

/arbre
{
  dup					% Sauvegarde la profondeur
  0 ne					% Test si fin de récursion
  {
    1 sub				% Calcule la nouvelle profondeur
    dup					% Duplique, car 2 appels récursif
    tronc				% Affiche le tronc
    gsave  0 100 translate  20 rotate .5 .5 scale arbre grestore
    gsave  0 100 translate -40 rotate .7 .7 scale arbre grestore
  }
  {
    pop					% Enlève le haut de pile
  }
  ifelse
} def    % La fonction récursive prend un argument dans la pile (profondeur)

200 0 translate
2 2 scale
11 arbre