La roue mecanum (inventé en 1973 wikipedia est une roue omni-directionnelle (ou holonome) permettant à un véhicule de se diriger dans toutes les directions: aussi bien sur le côté que vers l'avant et l'arrière, en ayant un axe de rotation fixe. Elle est très utilisée en robotique. Le principe est d'ajouter de petites roues sur la périphérie avec une axe de rotation à 45 degré et une rotation libre. Ce degré de liberté supplémentaire permet un roulement sans glissement de la roue dans toutes les directions sans avoir à tourner l'axe de rotation comme pour une roue classique.
Le robot utilisé "Raspblock" est proposé en kit par la société Yahboom et en ajoutant une carte Rasberry Pi 4, on obtiens un robot contrôlable en WIFI et programmable en Python. Ce robot éducatif basé sur Raspberry Pi 4B, utilise des roues Mecanum et des moteurs TT avec encodeur pour obtenir un mouvement omnidirectionnel à 360°. Il est de plus équipé d'une caméra caméra USB HQ mobille sur tourelle. Il embarque une carte d'extension avec des gyroscopes, des servos-moteurs, un haut-parleur et une interface moteur. Il embarque aussi un serveur Jupyter lab permettant sa programmation en python à distance en utilisant le WIFI.
La roue mecanum permet d'obtenir une vitesse à $\pm 45^o$ par rapport à la roue, avec une composante dans la direction de la roue et une composante dans la direction perpendiculaire: la direction dépendant du sens de rotation de la roue.
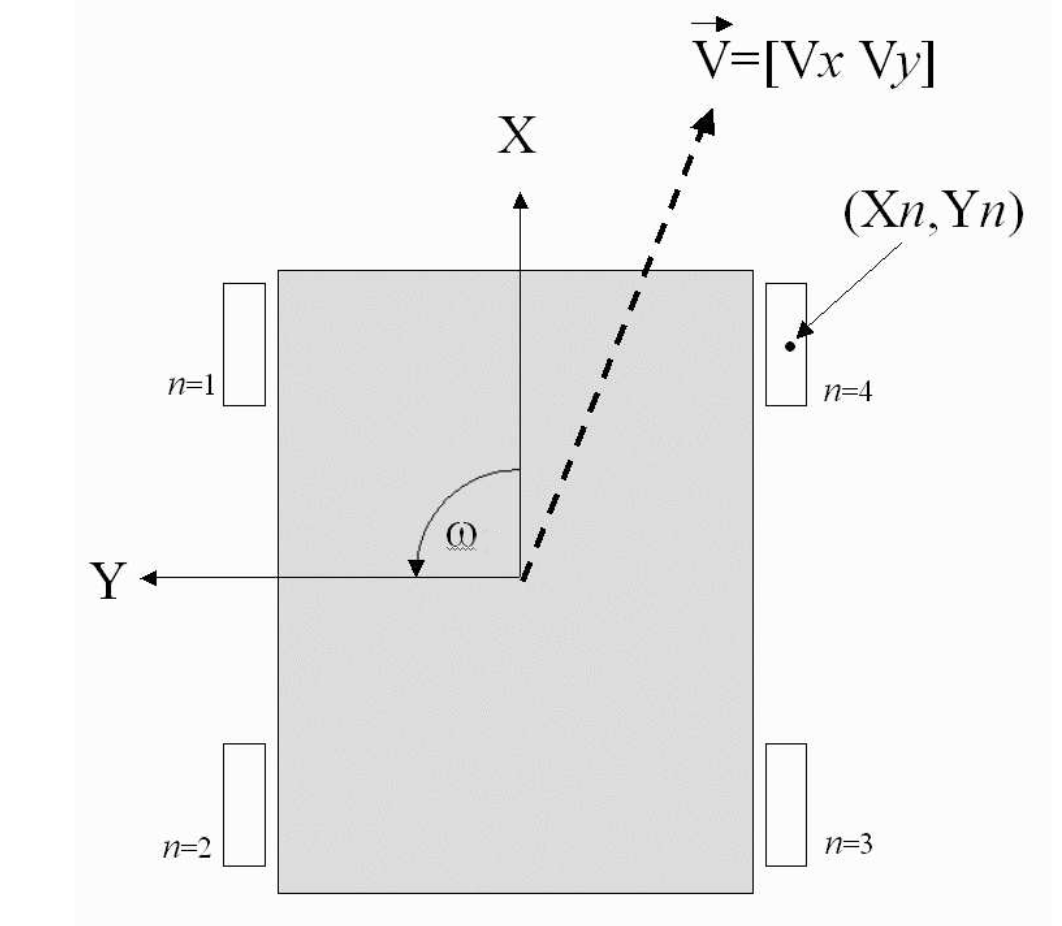
La combinaison des vitesses des 4 roues mecanum permet alors d'imposer la vitesse $\mathbf{V_G}=[V_x,V_y]$ du centre de gravité $G$ du robot ainsi que son taux de rotation $\Omega$ dans le repère lié au robot. A condition de choisir les bonnes vitesses de rotation $\boldsymbol{\omega}=[\omega_1, \omega_2,\omega_3,\omega_4]$ des 4 roues mecanum, on peut imposer n'importe quelle vitesse de déplacement $\mathbf{V_G}$ et de rotation $\Omega$ du robot.

Un modèle cinématique complet, avec une hypothèse de roulement sans glissement, permet d'obtenir ces vitesses de rotation $\boldsymbol{\omega}$ en se donnant $\mathbf{V_G}$ et $\Omega$. IL suffit de convertir ces valeurs en commandes des moteurs TT pour obtenir le déplacement du robot.
on utilise une bibliothèque ControlRaspblock qui implémente le modèle cinématique et permet de contrôler le robot.
Plusieurs trajectoires ont été testées et sont présentées dans la suite
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from IPython.display import IFrame
plt.rc('font', family='serif', size='16')
# modèle cinématique et ebvie des commandes au robot
from ControlRaspblock import ControlRaspblock, send_cdes
CRp = ControlRaspblock()
print(CRp)
Raspblock L=0.07m W=0.065m R=0.04m : Cmax=20 Wmax=20.0rd/s Umax=0.8m/s Omegamax=2.9rd/s
le centre de gravité du robot décrit un cercle sans effectuer de rotation propre du chassis. Le mouvement du robot est donc une translation sur une trajectoire circulaire.
RC = 0.8; OmegaC = 2*np.pi/20; Umax= RC*OmegaC
Tf = 20
N = int(Tf/CRp.dt)
TT = np.linspace(0,Tf,N,endpoint=False)
print("Um={:.2f} Umax={:.2f} Cde={:.1f} N:{} Tf={}".format(Umax,CRp.Umax,CRp.Cmax*Umax/CRp.Umax,N,Tf))
# vitesse
VX = RC*OmegaC*np.cos(OmegaC*TT)
VY = RC*OmegaC*np.sin(OmegaC*TT)
OMEGA = np.zeros(TT.size)
plt.figure(figsize=(14,8))
plt.subplot(1,2,1)
plt.plot(TT,VX,label="Ux")
plt.plot(TT,VY,label="Uy")
plt.plot(TT,OMEGA,label="Omega")
plt.legend()
plt.title("prediction vitesse")
# trajectoire predite
CRp.trajectoire(VX,VY,OMEGA)
plt.subplot(1,2,2)
CRp.plot_trajectoire()
plt.title("prediction trajectoire");
Um=0.25 Umax=0.80 Cde=6.3 N:200 Tf=20
# commandes
CDES = CRp.commandes(VX,VY,OMEGA)
plt.figure(figsize=(18,8))
plt.subplot(1,2,1)
plt.plot(TT,CDES[:,0],label="u1")
plt.plot(TT,CDES[:,1],label="u2")
plt.plot(TT,CDES[:,2],label="u3")
plt.plot(TT,CDES[:,3],label="u4")
plt.xlabel('t [sec]')
plt.legend()
plt.title("commandes des roues")
CRp.trajectoire(VX,VY,OMEGA)
plt.subplot(1,2,2)
CRp.plot_trajectoire()
plt.axis('off')
plt.title("Trajectoire souhaitée");
# envoie des cdes au robot
send_cdes(CDES)
# video du mouvement du robot
IFrame("https://mediacenter.univ-lyon1.fr/videos/?video=MEDIA210926104655828",640,360)
le centre de gravité du robot décrit un cercle mais en maintenant son axe X tangent au cercle, comme une voiture. Le mouvement du robot est donc une rotation pure.
VX = RC*OmegaC*np.ones(TT.size)
VY = np.zeros(TT.size)
OMEGA = OmegaC*np.ones(TT.size)
# trajectoire predite
plt.figure(figsize=(14,8))
plt.subplot(1,2,1)
plt.plot(TT,VX,label="Ux")
plt.plot(TT,VY,label="Uy")
plt.plot(TT,OMEGA,label="Omega")
plt.legend()
plt.title("prediction vitesse")
# trajectoire predite
CRp.trajectoire(VX,VY,OMEGA)
plt.subplot(1,2,2)
CRp.plot_trajectoire()
plt.title("prediction trajectoire");
# commandes
CDES = CRp.commandes(VX,VY,OMEGA)
plt.figure(figsize=(18,8))
plt.subplot(1,2,1)
plt.plot(TT,CDES[:,0],lw=2,label="u1")
plt.plot(TT,CDES[:,1],lw=2,label="u2")
plt.plot(TT,CDES[:,2],lw=2,label="u3")
plt.plot(TT,CDES[:,3],lw=2,label="u4")
plt.xlabel('t [sec]')
plt.legend()
plt.title("commandes des roues")
CRp.trajectoire(VX,VY,OMEGA)
plt.subplot(1,2,2)
CRp.plot_trajectoire()
plt.axis('off')
plt.title("Trajectoire souhaitée");
# envoie des cdes au robot
send_cdes(CDES)
# video du mouvement du robot
IFrame("https://mediacenter.univ-lyon1.fr/videos/?video=MEDIA210926151609653",640,360)
le centre de gravité du robot décrit un carré mais sans effectuer de rotation du chassis. Le mouvement du robot est donc une translation sur une trajectoire carrée.
# coté
RC = 1.2; Umax= CRp.Umax/3
Tf = 4*5
N = int(Tf/CRp.dt/4)
print("Um={:.2f} Umax={:.2f} Cde={:.1f} N={} Tf={}".format(Umax,CRp.Umax,CRp.Cmax*Umax/CRp.Umax,N,Tf))
TT = np.linspace(0,Tf,4*N,endpoint=False)
VX = np.zeros(TT.size)
VY = np.zeros(TT.size)
OMEGA = np.zeros(TT.size)
# vitesse / cote
VX[0:N] = Umax
VY[N:2*N] = Umax
VX[2*N:3*N] = -Umax
VY[3*N:] = -Umax
plt.figure(figsize=(14,8))
plt.subplot(1,2,1)
plt.plot(TT,VX,label="Ux")
plt.plot(TT,VY,label="Uy")
plt.plot(TT,OMEGA,label="Omega")
plt.legend()
plt.title("prediction vitesse")
# trajectoire predite
CRp.trajectoire(VX,VY,OMEGA)
plt.subplot(1,2,2)
CRp.plot_trajectoire()
plt.title("prediction trajectoire");
Um=0.27 Umax=0.80 Cde=6.7 N=50 Tf=20
# commandes
CDES = CRp.commandes(VX,VY,OMEGA)
plt.figure(figsize=(18,8))
plt.subplot(1,2,1)
plt.plot(TT,CDES[:,0],lw=2,label="u1")
plt.plot(TT,CDES[:,1],lw=2,label="u2")
plt.plot(TT,CDES[:,2],lw=2,label="u3")
plt.plot(TT,CDES[:,3],lw=2,label="u4")
plt.xlabel('t [sec]')
plt.legend()
plt.title("commandes des roues")
CRp.trajectoire(VX,VY,OMEGA)
plt.subplot(1,2,2)
CRp.plot_trajectoire()
plt.axis('off')
plt.title("Trajectoire souhaitée");
# envoie des cdes au robot
send_cdes(CDES)
# video du mouvement du robot
IFrame("https://mediacenter.univ-lyon1.fr/videos/?video=MEDIA210926151818690",640,360)
le centre de gravité du robot décrit un carré mais il maintient son axe X parallèle au coté du carré. Il doit donc effectuer une rotation à la fin de chaque coté. Le mouvement du robot est donc une translation + rotation sur une trajectoire carrée.
TT = np.linspace(0,Tf,4*N+5,endpoint=False)
VX = np.zeros(TT.size)
VY = np.zeros(TT.size)
OMEGA = np.zeros(TT.size)
# vitesse / cote
pas=5
VX[0+pas:N-pas] = Umax
VX[N+pas:2*N-pas] = Umax
VX[2*N+pas:3*N-pas]= Umax
VX[3*N+pas:4*N-pas]= Umax
# rotation de pi/2 sur 10 dt
OMEGA[N-pas:N+pas] = np.pi/2.
OMEGA[2*N-pas:2*N+pas] = np.pi/2.
OMEGA[3*N-pas:3*N+pas] = np.pi/2.
OMEGA[4*N-pas:] = np.pi/2.
#
plt.figure(figsize=(14,8))
plt.subplot(1,2,1)
plt.plot(TT,VX,label="Ux")
plt.plot(TT,VY,label="Uy")
plt.plot(TT,OMEGA,label="Omega")
plt.legend()
plt.title("prediction vitesse")
# trajectoire predite
CRp.trajectoire(VX,VY,OMEGA)
plt.subplot(1,2,2)
CRp.plot_trajectoire()
plt.title("prediction trajectoire");
# commandes
CDES = CRp.commandes(VX,VY,OMEGA)
plt.figure(figsize=(18,8))
plt.subplot(1,2,1)
plt.plot(TT,CDES[:,0],lw=2,label="u1")
plt.plot(TT,CDES[:,1],lw=2,label="u2")
plt.plot(TT,CDES[:,2],lw=2,label="u3")
plt.plot(TT,CDES[:,3],lw=2,label="u4")
plt.xlabel('t [sec]')
plt.legend()
plt.title("commandes des roues")
CRp.trajectoire(VX,VY,OMEGA)
plt.subplot(1,2,2)
CRp.plot_trajectoire()
plt.axis('off')
plt.title("Trajectoire souhaitée");
# envoie des cdes au robot
send_cdes(CDES)
# video du mouvement du robot
IFrame("https://mediacenter.univ-lyon1.fr/videos/?video=MEDIA210926152004981",640,360)