Cinématique d'une voiture à roue mecanum

(C) Marc BUFFAT, Département mécanique, Lyon 1

Table des matières

In [1]:
%matplotlib inline
import numpy as np
import sympy as sp
import k3d
import matplotlib.pyplot as plt
# bibliotheque mecanique
from sympy.physics.mechanics import dynamicsymbols, Point, ReferenceFrame
from sympy.physics.mechanics import Particle, RigidBody, inertia
from sympy.physics.mechanics import linear_momentum, angular_momentum
from sympy.physics.vector import time_derivative,dot
from sympy.physics.vector import init_vprinting
init_vprinting(use_latex='mathjax', pretty_print=False)

Modèle cinématique

La roue mecanum (inventé en 1973 wikipedia) est une roue omni-directionnelle (ou holonome) permettant à un véhicule de se diriger dans toutes les directions: aussi bien sur le côté que vers l'avant et l'arrière, en ayant un axe de rotation fixe. Elle est très utilisée en robotique. Le principe est d'ajouter de petites roues sur la périphérie avec un axe de rotation à 45 degré et une rotation libre. Ce degré de liberté supplémentaire permet un roulement sans glissement de la roue dans toutes les directions sans avoir à tourner l'axe de rotation comme pour une roue classique.

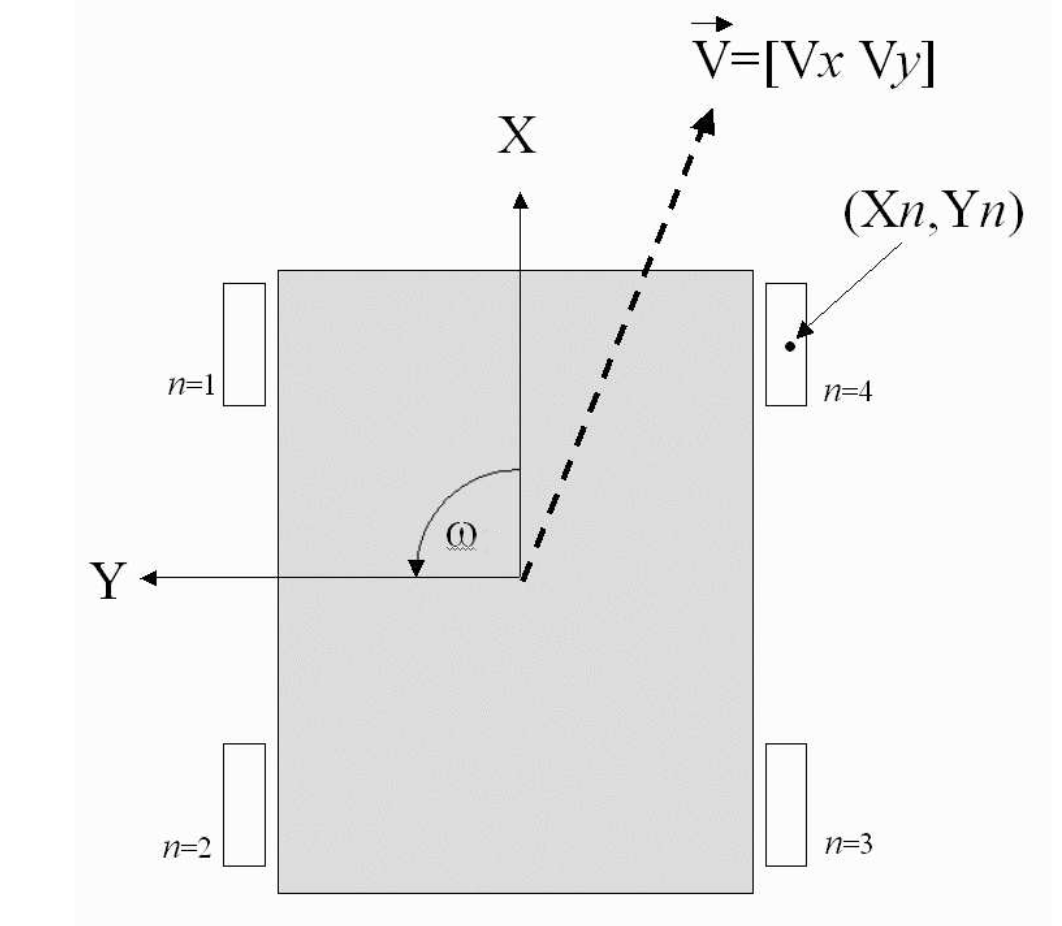
mecanum

La vitesse dans le repère R1 lié à la voiture du centre de gravité est: $$ \vec{V_G} = V_x \vec{R.x} + V_y \vec{R.y}$$ on note $\theta$ la rotation autour de R1.z de vitesse angulaire $\Omega$ $$ \Omega = \dot{\theta}$$

Soit $X_n,Y_n$ les coordonnées du centre de la roue $C_n$, la vitesse est $$ \vec{V_n} = \vec{V_G} + \Omega \vec{R1.z} \wedge \vec{GC_n} $$

La roue mecanum est constituée de petits rouleaux de rayon $r$ qui font un angle $\alpha_n = \pm 45$ degrés par rapport à $R1.x$. La rotation $\psi_n$ de ces rouleaux est libre et on suppose que le contacte au sol, en $I_n$ de coordonnées $<X_n,Y_n,-(R+r)>$, est ponctuel et sans glissement.

La vitesse au point de contact vaut:

$$ \vec{V}(I_n) = \vec{V_n} + \omega_n (R+r) \vec{Y_1} + r \dot{\psi_n} (\cos\theta_n \vec{Y_1} + \sin\theta_n \vec{X_1}) $$

La condition de roulement sans glissement au point $I_n$ impose $\vec{V}(I_n) =0$

ce qui donne pour la roue $C_1$ donne ($\theta_1 = -45$ degré)

$$ V_x - \Omega W - r \dot{\psi_1} \frac{\sqrt{2}}{2} = 0$$$$ V_y + \Omega L + \omega_1 (R+r) + r \dot{\psi_1} \frac{\sqrt{2}}{2} = 0$$

soit en éliminant $\dot{\psi_1}$ on obtiens (et en notant que $R \gg r$ une relation entre la vitesse de rotation $\omega_1$, la vitesse $\vec{V_G}$ et la rotation $\omega$ de la voiture: $$ V_x + V_y - \Omega (W-L) + \omega_1 (R+r)\approx V_x + V_y - \Omega (W-L) + \omega_1 R = 0$$

In [120]:
L,W,R,r= sp.symbols("L W R r")
t = sp.symbols('t')
theta = dynamicsymbols('theta')
# vitesse et rotation de la voiture
Vx,Vy,Omega = sp.symbols("V_x V_y Omega")

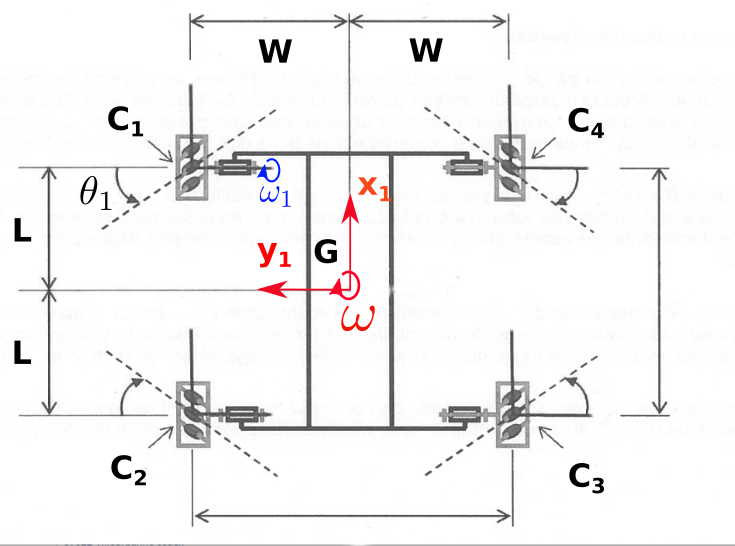
voiture mecanum

ATTENTION aux repères et aux orientations des axes

In [121]:
# repere voiture
R0 = ReferenceFrame("R_0")
O  = Point('O')
O.set_vel(R0,0)
# roue C1 avant gauche
R1 = ReferenceFrame("R_1")
R1.orient(R0,'Axis',[theta, R0.z])
G = Point('G')
G.set_vel(R0,Vx*R1.x + Vy*R1.y)

Relation de roulement sans glissement de la roue mecanum

On calcule la vitesse au point de contacte $I_1$ en fonction de la vitesse du robot ($V_x$, $V_y$ et $\Omega$), de la vitesse de rotation de la roue $\omega_1$ et de la vitesse de rotation du rouleau $\omega_I$.

La condition de roulement sans glissement impose l'annulation des 2 composantes de la vitesse en $I_1$, ce qui fixe la vitesse de rotation de la roue $\omega_1$ et de la vitesse de rotation du rouleau $\omega_I$ en fonction de la vitesse du robot ($V_x$, $V_y$ et $\Omega$).

En combinant les équations on élimine $\omega_I$ et on obtiens ainsi la relation de contrôle qui relie la vitesse de rotation de la roue $\omega_1$ et la vitesse du robot ($V_x$, $V_y$ et $\Omega$), que l'on simplifie en négligeant $r \ll R$

In [59]:
# point C1 roue avant gauche
C1 = Point("C_1")
C1.set_pos(G,L*R1.x + W*R1.y)
theta1 = - sp.pi/4
I1 = Point("I_1")
I1.set_pos(C1,-(R+r)*R0.z)
# vitesse de C1
VC1 = G.vel(R0) + (Omega*R1.z ^ C1.pos_from(G))
display("V(C1)=",VC1)
# vitesse de I1
omega1, omegaI = sp.symbols("omega_1 omega_I")
VI1 = VC1 + omega1*(R+r)*R1.y + omegaI*r*(sp.cos(theta1)*R1.x - sp.sin(theta1)*R1.y)
display("pt de contacte V(I1)=",VI1)

'V(C1)='
$\displaystyle (- \Omega W + V_{x})\mathbf{\hat{r_1}_x} + (L \Omega + V_{y})\mathbf{\hat{r_1}_y}$ 
'pt de contacte V(I1)='
$\displaystyle (- \Omega W + V_{x} + \frac{\sqrt{2} \omega_{I} r}{2})\mathbf{\hat{r_1}_x} + (L \Omega + V_{y} + \omega_{1} \left(R + r\right) + \frac{\sqrt{2} \omega_{I} r}{2})\mathbf{\hat{r_1}_y}$
In [56]:
# relation vitesse: cdt de roulement sans glissement en I1 avec r<<R
eq1=VI1.dot(R1.x)-VI1.dot(R1.y)
display(sp.Eq(eq1,0))
eq1 = eq1.subs(r,0)
display(sp.Eq(eq1,0))
Omega1 = sp.solve(eq1,omega1)[0]
sp.Eq(omega1,Omega1)
$\displaystyle - L \Omega - \Omega W + V_{x} - V_{y} - \omega_{1} \left(R + r\right) = 0$
$\displaystyle - L \Omega - \Omega W - R \omega_{1} + V_{x} - V_{y} = 0$
Out[56]:
$\displaystyle \omega_{1} = \frac{- L \Omega - \Omega W + V_{x} - V_{y}}{R}$
In [61]:
# points C2 arriere gauche
C2 = Point("C_2")
C2.set_pos(G,-L*R1.x + W*R1.y)
theta2 = + sp.pi/4
I2 = Point("I_2")
I2.set_pos(C2,-(R+r)*R0.z)
# vitesse de C2
VC2 = G.vel(R0) + (Omega*R1.z ^ C2.pos_from(G))
display("V(C2)=",VC2)
# vitesse de I2
omega2 = sp.symbols("omega_2")
VI2 = VC2 - omega2*(R+r)*R1.y + omegaI*r*(sp.cos(theta2)*R1.x - sp.sin(theta2)*R1.y)
display("pt de contacte V(I2)=",VI2)

'V(C2)='
$\displaystyle (- \Omega W + V_{x})\mathbf{\hat{r_1}_x} + (- L \Omega + V_{y})\mathbf{\hat{r_1}_y}$ 
'pt de contacte V(I2)='
$\displaystyle (- \Omega W + V_{x} + \frac{\sqrt{2} \omega_{I} r}{2})\mathbf{\hat{r_1}_x} + (- L \Omega + V_{y} - \omega_{2} \left(R + r\right) - \frac{\sqrt{2} \omega_{I} r}{2})\mathbf{\hat{r_1}_y}$
In [64]:
# relation vitesse cdt de roulement sans glissement en I2 avec r<<R
eq2=VI2.dot(R1.x)+VI2.dot(R1.y)
display(sp.Eq(eq2,0))
eq2=eq2.subs(r,0)
display(sp.Eq(eq2,0))
Omega2 = sp.solve(eq2,omega2)[0]
sp.Eq(omega2,Omega2)
$\displaystyle - L \Omega - \Omega W + V_{x} + V_{y} - \omega_{2} \left(R + r\right) = 0$
$\displaystyle - L \Omega - \Omega W - R \omega_{2} + V_{x} + V_{y} = 0$
Out[64]:
$\displaystyle \omega_{2} = \frac{- L \Omega - \Omega W + V_{x} + V_{y}}{R}$
In [65]:
# points C3 arriere droit
C3 = Point("C_3")
C3.set_pos(G,-L*R1.x - W*R1.y)
theta3 = - sp.pi/4
I3 = Point("I_3")
I3.set_pos(C3,-(R+r)*R0.z)
# vitesse de C2
VC3 = G.vel(R0) + (Omega*R1.z ^ C3.pos_from(G))
display("V(C3)=",VC3)
# vitesse de I3
omega3 = sp.symbols("omega_3")
VI3 = VC3 + omega3*(R+r)*R1.y + omegaI*r*(sp.cos(theta3)*R1.x - sp.sin(theta3)*R1.y)
display("pt de contacte V(I3)=",VI3)

'V(C3)='
$\displaystyle (\Omega W + V_{x})\mathbf{\hat{r_1}_x} + (- L \Omega + V_{y})\mathbf{\hat{r_1}_y}$ 
'pt de contacte V(I3)='
$\displaystyle (\Omega W + V_{x} + \frac{\sqrt{2} \omega_{I} r}{2})\mathbf{\hat{r_1}_x} + (- L \Omega + V_{y} + \omega_{3} \left(R + r\right) + \frac{\sqrt{2} \omega_{I} r}{2})\mathbf{\hat{r_1}_y}$
In [68]:
# relation vitesse cdt de roulement sans glissement en I3 avec r<<R
eq3=VI3.dot(R1.x)-VI3.dot(R1.y)
display(sp.Eq(eq3,0))
eq3 = eq3.subs(r,0)
display(sp.Eq(eq3,0))
Omega3 = sp.solve(eq3,omega3)[0]
sp.Eq(omega3,Omega3)
$\displaystyle L \Omega + \Omega W + V_{x} - V_{y} - \omega_{3} \left(R + r\right) = 0$
$\displaystyle L \Omega + \Omega W - R \omega_{3} + V_{x} - V_{y} = 0$
Out[68]:
$\displaystyle \omega_{3} = \frac{L \Omega + \Omega W + V_{x} - V_{y}}{R}$
In [69]:
# points C4 avant droit
C4 = Point("C_4")
C4.set_pos(G,+L*R1.x - W*R1.y)
theta4 = + sp.pi/4
I4 = Point("I_4")
I4.set_pos(C4,-(R+r)*R0.z)
# vitesse de C4
VC4 = G.vel(R0) + (Omega*R1.z ^ C4.pos_from(G))
display("V(C4)=",VC4)
# vitesse de I4
omega4 = sp.symbols("omega_4")
VI4 = VC4 - omega4*(R+r)*R1.y + omegaI*r*(sp.cos(theta4)*R1.x - sp.sin(theta4)*R1.y)
display("pt de contacte V(I4)=",VI4)

'V(C4)='
$\displaystyle (\Omega W + V_{x})\mathbf{\hat{r_1}_x} + (L \Omega + V_{y})\mathbf{\hat{r_1}_y}$ 
'pt de contacte V(I4)='
$\displaystyle (\Omega W + V_{x} + \frac{\sqrt{2} \omega_{I} r}{2})\mathbf{\hat{r_1}_x} + (L \Omega + V_{y} - \omega_{4} \left(R + r\right) - \frac{\sqrt{2} \omega_{I} r}{2})\mathbf{\hat{r_1}_y}$
In [72]:
# relation vitesse cdt de roulement sans glissement en I4 avec r<<R
eq4=VI4.dot(R1.x)+VI4.dot(R1.y)
display(sp.Eq(eq4,0))
eq4 = eq4.subs(r,0)
display(sp.Eq(eq4,0))
Omega4 = sp.solve(eq4,omega4)[0]
sp.Eq(omega4,Omega4)
$\displaystyle L \Omega + \Omega W + V_{x} + V_{y} - \omega_{4} \left(R + r\right) = 0$
$\displaystyle L \Omega + \Omega W - R \omega_{4} + V_{x} + V_{y} = 0$
Out[72]:
$\displaystyle \omega_{4} = \frac{L \Omega + \Omega W + V_{x} + V_{y}}{R}$
In [73]:
# d'où les 4 relations de controle
display(sp.Eq(eq1,0))
display(sp.Eq(eq2,0))
display(sp.Eq(eq3,0))
display(sp.Eq(eq4,0))
$\displaystyle - L \Omega - \Omega W - R \omega_{1} + V_{x} - V_{y} = 0$
$\displaystyle - L \Omega - \Omega W - R \omega_{2} + V_{x} + V_{y} = 0$
$\displaystyle L \Omega + \Omega W - R \omega_{3} + V_{x} - V_{y} = 0$
$\displaystyle L \Omega + \Omega W - R \omega_{4} + V_{x} + V_{y} = 0$

Relations de contrôle pour la vitesse

En combinant les relations précédentes, on calcule la vitesse $V_x$, $V_y$ et la rotation $\Omega$ du robot en fonctions de $\omega_1, \omega_2, \omega_3, \omega_4$

In [74]:
eq = eq1+eq2+eq3+eq4
display(eq)
VX=sp.solve(eq,Vx)[0]
sp.Eq(Vx,VX)
$\displaystyle - R \omega_{1} - R \omega_{2} - R \omega_{3} - R \omega_{4} + 4 V_{x}$
Out[74]:
$\displaystyle V_{x} = \frac{R \left(\omega_{1} + \omega_{2} + \omega_{3} + \omega_{4}\right)}{4}$
In [75]:
eq = eq2-eq1+eq4-eq3
display(eq)
VY=sp.solve(eq,Vy)[0]
sp.Eq(Vy,VY)
$\displaystyle R \omega_{1} - R \omega_{2} + R \omega_{3} - R \omega_{4} + 4 V_{y}$
Out[75]:
$\displaystyle V_{y} = \frac{R \left(- \omega_{1} + \omega_{2} - \omega_{3} + \omega_{4}\right)}{4}$
In [76]:
eq = (eq1+eq2)-(eq3+eq4)
display(eq)
OMEGA=sp.solve(eq,Omega)[0]
sp.Eq(Omega,OMEGA)
$\displaystyle - 4 L \Omega - 4 \Omega W - R \omega_{1} - R \omega_{2} + R \omega_{3} + R \omega_{4}$
Out[76]:
$\displaystyle \Omega = \frac{R \left(- \omega_{1} - \omega_{2} + \omega_{3} + \omega_{4}\right)}{4 \left(L + W\right)}$

cdts supplémentaire de non glissements

N'utilisant que 3 des relations précédentes, nous devons tenir compte d'une quatrième condition qui lie les vitesses de rotation $\omega_1, \omega_2, \omega_3, \omega_4$ permettant d'obtenir ce roulement sans glissement.

En effet on ne peut pas imposer des valeurs arbitraires $\omega_1, \omega_2, \omega_3, \omega_4$ pour contrôler la vitesse du robot (3 ddl). En reportant la valeur de la vitesse du robot $V_x, V_y, \Omega$ dans les 4 équations de contrôle, on obtiens la condition de compatibilité entre les rotations $\omega_1, \omega_2, \omega_3, \omega_4$ assurant le roulement sans glissement.

In [78]:
sp.Eq(eq1.subs({Omega:OMEGA,Vx:VX,Vy:VY}).simplify(),0)
Out[78]:
$\displaystyle \frac{R \left(- \omega_{1} + \omega_{2} + \omega_{3} - \omega_{4}\right)}{4} = 0$
In [79]:
sp.Eq(eq2.subs({Omega:OMEGA,Vx:VX,Vy:VY}).simplify(),0)
Out[79]:
$\displaystyle \frac{R \left(\omega_{1} - \omega_{2} - \omega_{3} + \omega_{4}\right)}{4} = 0$
In [80]:
sp.Eq(eq3.subs({Omega:OMEGA,Vx:VX,Vy:VY}).simplify(),0)
Out[80]:
$\displaystyle \frac{R \left(\omega_{1} - \omega_{2} - \omega_{3} + \omega_{4}\right)}{4} = 0$
In [81]:
sp.Eq(eq4.subs({Omega:OMEGA,Vx:VX,Vy:VY}).simplify(),0)
Out[81]:
$\displaystyle \frac{R \left(- \omega_{1} + \omega_{2} + \omega_{3} - \omega_{4}\right)}{4} = 0$
In [83]:
cdtsNG = eq3.subs({Omega:OMEGA,Vx:VX,Vy:VY}).simplify()*4/R
print("relation de compatibilité:")
display(sp.Eq(cdtsNG,0))

relation de compatibilité:
$\displaystyle \omega_{1} - \omega_{2} - \omega_{3} + \omega_{4} = 0$

Etude des mouvements possibles

Translation

On vérifie sur des mouvements simples les relations de contrôle

  1. vitesse suivant x: $V_x$ $$ \omega_1 = \omega_2 = \omega_3 = \omega_4 = \omega $$
  2. vitesse suivant y: $V_y$ $$ \omega_1 = -\omega_2 = \omega_3 = -\omega_4 = \omega $$
  3. vitesse oblique à 45° vers la droite $$ \omega_1 = \omega_3 = \omega \;,\; \omega_2 = -\omega_4 = 0 $$
  4. vitesse oblique à 45° vers la gauche $$ \omega_1 = \omega_3 = \omega \;,\; \omega_2 = \omega_4 = 0 $$
In [90]:
omega = sp.symbols('omega')
cdts = {omega1:omega,omega2:omega,omega3:omega,omega4:omega}
display(sp.Eq(Vx,VX.subs(cdts)))
display(sp.Eq(Vy,VY.subs(cdts)))
display(sp.Eq(Omega,OMEGA.subs(cdts)))
display("cdts de NG:",cdtsNG.subs(cdts))
$\displaystyle V_{x} = R \omega$
$\displaystyle V_{y} = 0$
$\displaystyle \Omega = 0$ 
'cdts de NG:'
$\displaystyle 0$
In [91]:
cdts = {omega1:omega,omega2:-omega,omega3:omega,omega4:-omega}
display(sp.Eq(Vx,VX.subs(cdts)))
display(sp.Eq(Vy,VY.subs(cdts)))
display(sp.Eq(Omega,OMEGA.subs(cdts)))
display("cdts de NG:",cdtsNG.subs(cdts))
$\displaystyle V_{x} = 0$
$\displaystyle V_{y} = - R \omega$
$\displaystyle \Omega = 0$ 
'cdts de NG:'
$\displaystyle 0$
In [92]:
cdts = {omega1:omega,omega2:0,omega3:omega,omega4:0}
display(sp.Eq(Vx,VX.subs(cdts)))
display(sp.Eq(Vy,VY.subs(cdts)))
display(sp.Eq(Omega,OMEGA.subs(cdts)))
display("cdts de NG:",cdtsNG.subs(cdts))
$\displaystyle V_{x} = \frac{R \omega}{2}$
$\displaystyle V_{y} = - \frac{R \omega}{2}$
$\displaystyle \Omega = 0$ 
'cdts de NG:'
$\displaystyle 0$
In [94]:
cdts = {omega1:0,omega2:omega,omega3:0,omega4:omega}
display(sp.Eq(Vx,VX.subs(cdts)))
display(sp.Eq(Vy,VY.subs(cdts)))
display(sp.Eq(Omega,OMEGA.subs(cdts)))
display("cdt de NG:",cdtsNG.subs(cdts))
$\displaystyle V_{x} = \frac{R \omega}{2}$
$\displaystyle V_{y} = \frac{R \omega}{2}$
$\displaystyle \Omega = 0$ 
'cdt de NG:'
$\displaystyle 0$

Rotation

de meme avec rotation

  1. rotation sur place $$ \omega_1 = \omega_2 = -\omega \;, \; \omega_3 = \omega_4 = \omega $$
  2. rotation et translation suivant x $$ \omega_1 = \omega_2 = -\omega \;, \; \omega_3 = \omega_4 = 0 $$
In [95]:
cdts = {omega1:-omega,omega2:-omega,omega3:omega,omega4:omega}
display(sp.Eq(Vx,VX.subs(cdts)))
display(sp.Eq(Vy,VY.subs(cdts)))
display(sp.Eq(Omega,OMEGA.subs(cdts)))
display("cdt de NG:",cdtsNG.subs(cdts))
$\displaystyle V_{x} = 0$
$\displaystyle V_{y} = 0$
$\displaystyle \Omega = \frac{R \omega}{L + W}$ 
'cdt de NG:'
$\displaystyle 0$
In [96]:
cdts = {omega1:-omega,omega2:-omega,omega3:0,omega4:0}
display(sp.Eq(Vx,VX.subs(cdts)))
display(sp.Eq(Vy,VY.subs(cdts)))
display(sp.Eq(Omega,OMEGA.subs(cdts)))
display("cdt de NG:",cdtsNG.subs(cdts))
$\displaystyle V_{x} = - \frac{R \omega}{2}$
$\displaystyle V_{y} = 0$
$\displaystyle \Omega = \frac{R \omega}{2 \left(L + W\right)}$ 
'cdt de NG:'
$\displaystyle 0$

mise sous forme matricielle

pour définir le contrôle du robot, on va cérire les relations précédentes sous forme matricielle

$$ [V_G] = \mathcal{A} [\omega]$$

avec $[V_G] = [V_x, V_y, \Omega, 0]$ et $[\omega]=[ \omega_1,\omega_2,\omega_3,\omega_4]$

On vérifie que le système est bien contrôlable (i.e. det(A) # 0), ce qui permet de l'inverser pour obtenir les commandes $[\omega]$ pour obtenir une mouvement fixée

$$ [\omega] = \mathcal{A}^{-1} [V_G]$$

In [98]:
from sympy.matrices import Matrix,zeros
In [99]:
display(VX.expand())
display(VY.expand())
display(OMEGA.expand())
display(cdtsNG)
$\displaystyle \frac{R \omega_{1}}{4} + \frac{R \omega_{2}}{4} + \frac{R \omega_{3}}{4} + \frac{R \omega_{4}}{4}$
$\displaystyle - \frac{R \omega_{1}}{4} + \frac{R \omega_{2}}{4} - \frac{R \omega_{3}}{4} + \frac{R \omega_{4}}{4}$
$\displaystyle - \frac{R \omega_{1}}{4 L + 4 W} - \frac{R \omega_{2}}{4 L + 4 W} + \frac{R \omega_{3}}{4 L + 4 W} + \frac{R \omega_{4}}{4 L + 4 W}$
$\displaystyle \omega_{1} - \omega_{2} - \omega_{3} + \omega_{4}$
In [97]:
A = Matrix([[R/4,R/4,R/4,R/4],[-R/4,R/4,-R/4,R/4],[-R/4/(L+W),-R/4/(L+W),R/4/(L+W),R/4/(L+W)],[1,-1,-1,1]])
display("A=",A)

'A='
$\displaystyle \left[\begin{matrix}\frac{R}{4} & \frac{R}{4} & \frac{R}{4} & \frac{R}{4}\\- \frac{R}{4} & \frac{R}{4} & - \frac{R}{4} & \frac{R}{4}\\- \frac{R}{4 \left(L + W\right)} & - \frac{R}{4 \left(L + W\right)} & \frac{R}{4 \left(L + W\right)} & \frac{R}{4 \left(L + W\right)}\\1 & -1 & -1 & 1\end{matrix}\right]$
In [101]:
display("det(A)=",A.det())

'det(A)='
$\displaystyle \frac{R^{3}}{4 L + 4 W}$
In [104]:
Ai = A.inv()
display("A-1=",Ai)

'A-1='
$\displaystyle \left[\begin{matrix}\frac{1}{R} & - \frac{1}{R} & \frac{- L - W}{R} & \frac{1}{4}\\\frac{1}{R} & \frac{1}{R} & \frac{- L - W}{R} & - \frac{1}{4}\\\frac{1}{R} & - \frac{1}{R} & \frac{L}{R} + \frac{W}{R} & - \frac{1}{4}\\\frac{1}{R} & \frac{1}{R} & \frac{L}{R} + \frac{W}{R} & \frac{1}{4}\end{matrix}\right]$

Vérification

In [32]:
OMEGAI = Ai * Matrix(4,1,[Vx,Vy,Omega,0])
display(OMEGAI)
$\displaystyle \left[\begin{matrix}\frac{\Omega \left(- L - W\right)}{R} + \frac{V_{x}}{R} - \frac{V_{y}}{R}\\\frac{\Omega \left(- L - W\right)}{R} + \frac{V_{x}}{R} + \frac{V_{y}}{R}\\\Omega \left(\frac{L}{R} + \frac{W}{R}\right) + \frac{V_{x}}{R} - \frac{V_{y}}{R}\\\Omega \left(\frac{L}{R} + \frac{W}{R}\right) + \frac{V_{x}}{R} + \frac{V_{y}}{R}\end{matrix}\right]$
In [33]:
VI = A*OMEGAI
for i in range(4):
    display(VI[i].simplify())
$\displaystyle V_{x}$
$\displaystyle V_{y}$
$\displaystyle \Omega$
$\displaystyle 0$
In [34]:
A*Matrix([1,-1,1,-1])
Out[34]:
$\displaystyle \left[\begin{matrix}0\\- R\\0\\0\end{matrix}\right]$
In [35]:
A*Matrix([omega1,omega2,omega3,omega4])
Out[35]:
$\displaystyle \left[\begin{matrix}\frac{R \omega_{1}}{4} + \frac{R \omega_{2}}{4} + \frac{R \omega_{3}}{4} + \frac{R \omega_{4}}{4}\\- \frac{R \omega_{1}}{4} + \frac{R \omega_{2}}{4} - \frac{R \omega_{3}}{4} + \frac{R \omega_{4}}{4}\\- \frac{R \omega_{1}}{4 \left(L + W\right)} - \frac{R \omega_{2}}{4 \left(L + W\right)} + \frac{R \omega_{3}}{4 \left(L + W\right)} + \frac{R \omega_{4}}{4 \left(L + W\right)}\\\omega_{1} - \omega_{2} - \omega_{3} + \omega_{4}\end{matrix}\right]$

Conclusion

Donc un un choix quelconque des vitesses de rotation $\omega_i$ ne conduit pas à un roulement sans glissement des roues, car la dernière relation n'est pas vérifiée.

Par contre on peut choisir arbitrairement $V_x, V_y, Omega$. Avec la condition de contrainte, on obtiens la valeur unique des vitesses de rotation $\omega_i$

Applications numériques

In [36]:
# dimension raspbloc (moteur TT DC ~ 100 rpm max)
wmax = sp.symbols("wmax")
params = { L : 0.14/2., W : 0.13/2.0, R : 0.06/2., wmax : 100.*2*np.pi/60.}
print(params)

{L: 0.07, W: 0.065, R: 0.03, wmax: 10.471975511965978}
In [105]:
# matrice de commande 
MC = np.array(A.subs(params),dtype=float)
display("MC=",MC)
print("det(MC)=",np.linalg.det(MC))
# matrice de contrôle
MI = np.array(Ai.subs(params),dtype=float)
display("MI=",MI)
print("det(MI)=",np.linalg.det(MI))

'MC='
array([[ 0.0075    ,  0.0075    ,  0.0075    ,  0.0075    ],
       [-0.0075    ,  0.0075    , -0.0075    ,  0.0075    ],
       [-0.05555556, -0.05555556,  0.05555556,  0.05555556],
       [ 1.        , -1.        , -1.        ,  1.        ]])
det(MC)= 5.000000000000004e-05

'MI='
array([[ 33.33333333, -33.33333333,  -4.5       ,   0.25      ],
       [ 33.33333333,  33.33333333,  -4.5       ,  -0.25      ],
       [ 33.33333333, -33.33333333,   4.5       ,  -0.25      ],
       [ 33.33333333,  33.33333333,   4.5       ,   0.25      ]])
det(MI)= 20000.00000000002
In [38]:
MC @ [-1,1,-1,1]
Out[38]:
array([0.  , 0.03, 0.  , 0.  ])
In [39]:
MI @ [0,1,0,0]
Out[39]:
array([-33.33333333,  33.33333333, -33.33333333,  33.33333333])

trajectoire circulaire (translation)

cas d'une trajectoire circulaire: mouvement de translation

  • $X_G = R_c \cos \omega_c t \;,\; Y_G = R_c \sin \omega_c t $

  • $V_X = -R_c \omega_c \sin \omega_c t \;,\; V_Y = R_c \omega_c \cos \omega_c t \;,\; \Omega = 0$

applications:

  • $R_c = 1/2 \;,\; \omega_c = 2\pi/60 $
  • 1 commande toutes les secondes
In [107]:
RC = 0.5; OmegaC = 2*np.pi/60
T = np.linspace(0,60,61)
VX = - RC*OmegaC*np.sin(OmegaC*T); VY = RC*OmegaC*np.cos(OmegaC*T); OMEGA = np.zeros(T.size)
In [108]:
plt.figure(figsize=(12,8))
plt.plot(T,VX,T,VY,T,OMEGA)
plt.title("Vitesse désirée");
In [109]:
Omega1 = np.zeros(T.size)
Omega2 = np.zeros(T.size)
Omega3 = np.zeros(T.size)
Omega4 = np.zeros(T.size)
for i in range(T.size):
    Vit = np.array([VX[i],VY[i],OMEGA[i],0.])
    OM  = MI.dot(Vit)
    Omega1[i] = OM[0]
    Omega2[i] = OM[1]
    Omega3[i] = OM[2]
    Omega4[i] = OM[3]
In [110]:
plt.figure(figsize=(12,8))
plt.plot(T,Omega1*30/np.pi,label="$\omega_1$")
plt.plot(T,Omega2*30/np.pi,label="$\omega_2$")
plt.plot(T,Omega3*30/np.pi,label="$\omega_3$")
plt.plot(T,Omega4*30/np.pi,label="$\omega_4$")
plt.plot(T,np.zeros(T.size),'--')
plt.legend()
plt.title("Rotations des roues (en rpm)");
In [111]:
def car(xg,yg,theta):
    h = 0.05
    w = 0.025
    # rotation de theta
    X0 = np.array([w, w,-w,-w,0])
    Y0 = np.array([h,-h,-h, h,1.5*h])
    c = np.cos(theta)
    s = np.sin(theta)
    X = X0*c - Y0*s
    Y = X0*s + Y0*c
    # translation
    X += xg
    Y += yg
    plt.fill(X,Y,"r")
    return
In [112]:
# calcul de la trajectoire par integration
dt = T[1]
XG = np.zeros(T.size)
YG = np.zeros(T.size)
THETA = np.zeros(T.size)
XG[0]=RC; YG[0]=0; THETA[0]=0
for i in range(1,T.size):
    XG[i] = XG[i-1] + dt*VX[i-1]
    YG[i] = YG[i-1] + dt*VY[i-1]
    THETA[i] = THETA[i-1] + dt*OMEGA[i-1]
In [113]:
plt.figure(figsize=(10,8))
plt.plot(XG,YG,lw=2)
for i in range(0,T.size,5):
    car(XG[i],YG[i],THETA[i])
plt.title("Trajectoire du robot")
plt.axis('equal');

trajectoire circulaire (rotation)

cas d'une trajectoire circulaire: mouvement de rotation

  • $X_G = R_c \cos \omega_c t \;,\; Y_G = R_c \sin \omega_c t $

  • $V_X = -R_c \omega_c \sin \omega_c t \;,\; V_Y = R_c \omega_c \cos \omega_c t \;,\; \Omega = \omega_c$

In [114]:
RC = 0.5; OmegaC = 2*np.pi/60
T = np.linspace(0,60,61)
VX = - RC*OmegaC*np.sin(OmegaC*T); VY = RC*OmegaC*np.cos(OmegaC*T); OMEGA = 2*OmegaC*np.ones(T.size)
In [115]:
plt.figure(figsize=(12,8))
plt.plot(T,VX,T,VY,T,OMEGA)
plt.title("Vitesse désirée");
In [116]:
Omega1 = np.zeros(T.size)
Omega2 = np.zeros(T.size)
Omega3 = np.zeros(T.size)
Omega4 = np.zeros(T.size)
for i in range(T.size):
    Vit = np.array([VX[i],VY[i],OMEGA[i],0.])
    OM  = MI.dot(Vit)
    Omega1[i] = OM[0]
    Omega2[i] = OM[1]
    Omega3[i] = OM[2]
    Omega4[i] = OM[3]
In [117]:
plt.figure(figsize=(12,8))
plt.plot(T,Omega1*30/np.pi,label="$\omega_1$")
plt.plot(T,Omega2*30/np.pi,label="$\omega_2$")
plt.plot(T,Omega3*30/np.pi,label="$\omega_3$")
plt.plot(T,Omega4*30/np.pi,label="$\omega_4$")
plt.plot(T,np.zeros(T.size),'--')
plt.legend()
plt.title("Rotations des roues (en rpm)");
In [118]:
# calcul de la trajectoire par integration
dt = T[1]
XG = np.zeros(T.size)
YG = np.zeros(T.size)
THETA = np.zeros(T.size)
XG[0]=RC; YG[0]=0;
for i in range(1,T.size):
    XG[i] = XG[i-1] + dt*VX[i-1]
    YG[i] = YG[i-1] + dt*VY[i-1]
    THETA[i] = THETA[i-1] + dt*OMEGA[i-1]
In [119]:
plt.figure(figsize=(10,8))
plt.plot(XG,YG,lw=2)
for i in range(0,T.size,5):
    car(XG[i],YG[i],THETA[i])
plt.title("Trajectoire du robot")
plt.axis('equal');

références

  1. Uwe Kiencke et Lars Nielsen, "Automotive Control Systems", springer 2005
  2. Salim Maakaroun,, "Modélisation et simulation dynamique d’un véhicule urbain innovant en utilisant le formalisme de la robotique", Ecole des Mines de Nantes, 2011
  3. Eka Maulana, M. Aziz Muslim, Veri Hendrayawan, "Inverse kinematic implementation of four-wheels mecanum drive mobile robot using stepper motors" Conference: 2015 International Seminar on Intelligent Technology and Its Applications (ISITIA)
  4. "Kinematic Analysis of Four-Wheel Mecanum Vehicle", Ether, 2005
  5. N. Morette, "Contribution à la Navigation de robots mobiles : approche par modèle direct et commande prédictive", thèse 2009, Université Orléans.

FIN