> restart:with(Student[LinearAlgebra]):with(plots):with(plottools):

Warning, the protected name . has been redefined and unprotected

Warning, the name changecoords has been redefined

Warning, the name arrow has been redefined

> alias(theta=theta(t),phi=phi(t),psi=psi(t));

theta, phi, psi

Etude du mouvement gyroscopique de la toupie

mouvement d'une toupie tournant sur son axe de rotation autour d'un point O sans frottement

Définition des Reperes

Repere fixe R0 (X0,Y0,Z0)

Repere mobile R1: rotation theta autour de Z, vecteur rotation et matrice de passage de R0->R1  (cpste de R1 dans R0)
theta= angle de precession

> Omega10:=<0,0,diff(theta,t)>;
M01:=<<cos(theta),sin(theta),0>|<-sin(theta),cos(theta),0>|<0,0,1>>;
M10:=Transpose(M01);

Omega10 := Vector[column]([[0], [0], [diff(theta, t)]])

M01 := Matrix([[cos(theta), -sin(theta), 0], [sin(theta), cos(theta), 0], [0, 0, 1]])

M10 := Matrix([[cos(theta), sin(theta), 0], [-sin(theta), cos(theta), 0], [0, 0, 1]])

Repere mobile R2: rotation phi autour de Y1
phi= angle de nutation (variation d'obliquité de la toupie)

> Omega21:=<0,diff(phi,t),0>;
M12:=<<cos(phi),0,-sin(phi)>|<0,1,0>|<sin(phi),0,cos(phi)>>;
M21:=Transpose(M12);

Omega21 := Vector[column]([[0], [diff(phi, t)], [0]])

M12 := Matrix([[cos(phi), 0, sin(phi)], [0, 1, 0], [-sin(phi), 0, cos(phi)]])

M21 := Matrix([[cos(phi), 0, -sin(phi)], [0, 1, 0], [sin(phi), 0, cos(phi)]])

Vecteur rotation de R2/R0

> Omega20:=Omega21+M21.Omega10;

Omega20 := Vector[column]([[-sin(phi)*diff(theta, t)], [diff(phi, t)], [cos(phi)*diff(theta, t)]])

Repere lie au solide R3: rotation psi autour de Z2

psi= rotation propre

> Omega32:=<0,0,diff(psi,t)>;

Omega32 := Vector[column]([[0], [0], [diff(psi, t)]])

>

Coordonnees de la toupie dans R0

> OG:=M01.(M12.<0,0,l>);

OG := Vector[column]([[cos(theta)*sin(phi)*l], [sin(theta)*sin(phi)*l], [cos(phi)*l]])

> Toupie:=proc(Theta,Phi)
local OG;
OG:=vector([cos(Theta)*sin(Phi),sin(Theta)*sin(Phi),cos(Phi)]);
arrow(vector([0, 0, 0]),OG,0.05, 0.4, .0, cylindrical_arrow)
end proc:

> display(Toupie(Pi/4,Pi/6),scaling=CONSTRAINED, axes=BOXED,labels=[X,Y,Z],title="toupie",orientation=[32,63]);

[Plot]

Visualisation des reperes

>

> repere:=proc(M,c)
local u1,u2,u3;
 u1:=M.<1,0,0>:
 u2:=M.<0,1,0>:
 u3:=M.<0,0,1>:
 arrow(vector([0,0,0]),convert(u1,vector),.1, .2, .1,cylindrical_arrow,color=c),
 arrow(vector([0,0,0]),convert(u2,vector),.1, .2, .1,cylindrical_arrow,color=c),
 arrow(vector([0,0,0]),convert(u3,vector),.1, .2, .1,cylindrical_arrow,color=c):
end proc:

> PR0:=repere(<<1,0,0>|<0,1,0>|<0,0,1>>,black):
PR1:=repere(subs(theta=Pi/4,M01),blue):
PR2:=repere(subs(theta=Pi/4,phi=Pi/6,M01.M12),red):
display({PR0,PR1},scaling=CONSTRAINED, axes=BOXED,labels=[X,Y,Z],title="repere R1",orientation=[32,63]);
display({PR0,PR1,PR2},scaling=CONSTRAINED, axes=BOXED,labels=[X,Y,Z],title="repere R2",orientation=[32,63]);

[Plot]

[Plot][Plot]

>

Mise en équation
vecteur rotation instantané dans R2 et vitesse de G

> Omega:=Omega32+Omega21+M21.Omega10;

Omega := Vector[column]([[-sin(phi)*diff(theta, t)], [diff(phi, t)], [diff(psi, t)+cos(phi)*diff(theta, t)]])

> OG:=<0,0,l>; VG:=Omega &x OG;

OG := Vector[column]([[0], [0], [l]])

VG := Vector[column]([[diff(phi, t)*l], [sin(phi)*diff(theta, t)*l], [0]])

moment cinétique en G (Z2 axe de revolution), puis en O

> MI:=<<I2,0,0>|<0,I2,0>|<0,0,I1>>;

MI := Matrix([[I2, 0, 0], [0, I2, 0], [0, 0, I1]])

> sigma:=MI.Omega;

sigma := Vector[column]([[-I2*sin(phi)*diff(theta, t)], [I2*diff(phi, t)], [I1*(diff(psi, t)+cos(phi)*diff(theta, t))]])

> sigma0:=sigma + OG &x (m*VG);

sigma0 := Vector[column]([[-I2*sin(phi)*diff(theta, t)-l^2*m*sin(phi)*diff(theta, t)], [I2*diff(phi, t)+l^2*m*diff(phi, t)], [I1*(diff(psi, t)+cos(phi)*diff(theta, t))]])

> I20=I2+m*l^2;

I20 = I2+m*l^2

> sigma0:=simplify(subs(I2=I20-m*l^2,sigma0));

sigma0 := Vector[column]([[-sin(phi)*diff(theta, t)*I20], [diff(phi, t)*I20], [I1*(diff(psi, t)+cos(phi)*diff(theta, t))]])

>

Energie cinetique

> Ec:=1/2*sigma0.Omega;

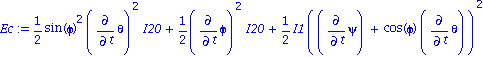
Ec := 1/2*sin(phi)^2*diff(theta, t)^2*I20+1/2*diff(phi, t)^2*I20+1/2*I1*(diff(psi, t)+cos(phi)*diff(theta, t))^2

moment du poid en O: Mo=OG*mg

> P:=M21.<0,0,-m*g>;

P := Vector[column]([[sin(phi)*m*g], [0], [-cos(phi)*m*g]])

> MP:=OG &x P;

MP := Vector[column]([[0], [l*sin(phi)*m*g], [0]])

Equation du mouvement dans R2

> map(diff,sigma0,t) + Omega20 &x sigma0 - MP=0;eq:=lhs(%):

Vector[column]([[-2*cos(phi)*diff(phi, t)*diff(theta, t)*I20-sin(phi)*diff(theta, `$`(t, 2))*I20+diff(phi, t)*I1*(diff(psi, t)+cos(phi)*diff(theta, t))], [diff(phi, `$`(t, 2))*I20-cos(phi)*diff(theta,...

Conservation du moment cinetique suivant Z2 (3ieme equation)

> sigma0[3]=omega*I1;eq3a:=%/I1:eq3a;
diff(psi,t)=solve(%,diff(psi,t)); rel1:=%:

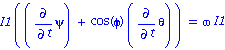
I1*(diff(psi, t)+cos(phi)*diff(theta, t)) = omega*I1

diff(psi, t)+cos(phi)*diff(theta, t) = omega

diff(psi, t) = -cos(phi)*diff(theta, t)+omega

Simplification equation 2 avec la 3ieme

> eq2:=simplify(subs(rel1,eq[2]));
eq2:=expand(eq2/I20);
k=I20/I1;rel2:=%:
B=l*m*g/I20; rel3:=%:
eq2:=subs(I1=I20/k,I20=l*m*g/B,eq2);eq2:=collect(%,sin(phi));
diff(phi,t$2)=collect(solve(%,diff(phi,t$2)),sin(phi));eq2a:=%:

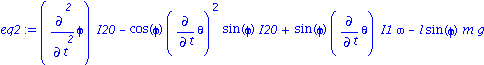
eq2 := diff(phi, `$`(t, 2))*I20-cos(phi)*diff(theta, t)^2*sin(phi)*I20+sin(phi)*diff(theta, t)*I1*omega-l*sin(phi)*m*g

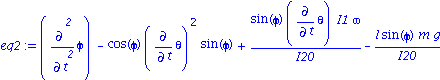
eq2 := diff(phi, `$`(t, 2))-cos(phi)*diff(theta, t)^2*sin(phi)+sin(phi)*diff(theta, t)*I1*omega/I20-l*sin(phi)*m*g/I20

k = I20/I1

B = l*m*g/I20

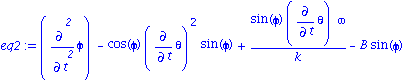
eq2 := diff(phi, `$`(t, 2))-cos(phi)*diff(theta, t)^2*sin(phi)+sin(phi)*diff(theta, t)*omega/k-B*sin(phi)

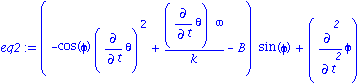
eq2 := (-cos(phi)*diff(theta, t)^2+diff(theta, t)*omega/k-B)*sin(phi)+diff(phi, `$`(t, 2))

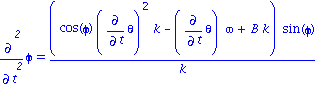
diff(phi, `$`(t, 2)) = (cos(phi)*diff(theta, t)^2*k-diff(theta, t)*omega+B*k)*sin(phi)/k

simplification de la 1ere equation avec la 3ieme

> eq1:=simplify(subs(rel1,eq[1]));
eq1:=expand(eq1/I20);eq1:=subs(I1=k*I20,%);
diff(theta,t$2)=solve(%,diff(theta,t$2));eq1a:=%:

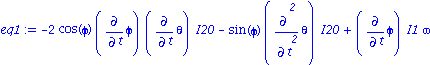
eq1 := -2*cos(phi)*diff(phi, t)*diff(theta, t)*I20-sin(phi)*diff(theta, `$`(t, 2))*I20+diff(phi, t)*I1*omega

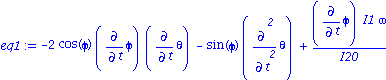
eq1 := -2*cos(phi)*diff(phi, t)*diff(theta, t)-sin(phi)*diff(theta, `$`(t, 2))+diff(phi, t)*I1*omega/I20

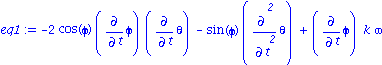
eq1 := -2*cos(phi)*diff(phi, t)*diff(theta, t)-sin(phi)*diff(theta, `$`(t, 2))+diff(phi, t)*k*omega

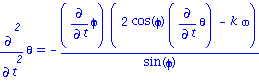
diff(theta, `$`(t, 2)) = -diff(phi, t)*(2*cos(phi)*diff(theta, t)-k*omega)/sin(phi)

Equations du mouvement

> eq1a; eq2a; eq3a;

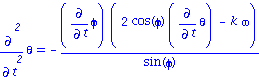
diff(theta, `$`(t, 2)) = -diff(phi, t)*(2*cos(phi)*diff(theta, t)-k*omega)/sin(phi)

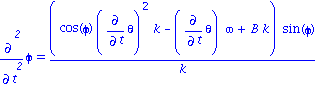
diff(phi, `$`(t, 2)) = (cos(phi)*diff(theta, t)^2*k-diff(theta, t)*omega+B*k)*sin(phi)/k

diff(psi, t)+cos(phi)*diff(theta, t) = omega

avec les parametres

> rel2; rel3;

k = I20/I1

B = l*m*g/I20

Recherche des Integrales premieres

Conservation du moment cinetique suivant Z2: 1ere IP

> eq3a; IP1:=%:

diff(psi, t)+cos(phi)*diff(theta, t) = omega

Conservation du moment cinetique suivant l'axe Z0 (//e au poid): 2ieme IP

> Z0:=M21.<0,0,1>;

Z0 := Vector[column]([[-sin(phi)], [0], [cos(phi)]])

> sigma0.Z0=omega*k0*I20; rel2; subs(I20=I1/k,expand(%%/I1)):collect(%,diff(theta,t));IP2:=%:

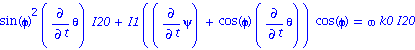
sin(phi)^2*diff(theta, t)*I20+I1*(diff(psi, t)+cos(phi)*diff(theta, t))*cos(phi) = omega*k0*I20

k = I20/I1

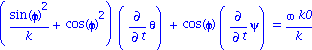
(sin(phi)^2/k+cos(phi)^2)*diff(theta, t)+cos(phi)*diff(psi, t) = omega*k0/k

En utilisant la première intégrale première, on obtiens la seconde IP

> simplify(IP2-IP1*cos(phi)):diff(theta,t)=solve(%,diff(theta,t));IP2:=%:

diff(theta, t) = -omega*(-k0+cos(phi)*k)/sin(phi)^2

conservation de l'energie totale: 3ieme IP

> U:=m*g*OG.Z0; rel2,rel3;

U := m*g*l*cos(phi)

k = I20/I1, B = l*m*g/I20

> E=Ec+U; IP3:=%: subs(diff(psi,t)=solve(IP1,diff(psi,t)),IP3);
IP3:=subs(I1=I20/k,I20=l*m*g/B,expand(%/I20-(omega^2/2/k=omega^2/2/k))):IP3;

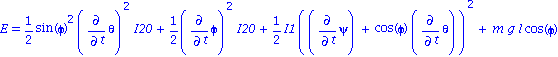
E = 1/2*sin(phi)^2*diff(theta, t)^2*I20+1/2*diff(phi, t)^2*I20+1/2*I1*(diff(psi, t)+cos(phi)*diff(theta, t))^2+m*g*l*cos(phi)

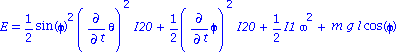
E = 1/2*sin(phi)^2*diff(theta, t)^2*I20+1/2*diff(phi, t)^2*I20+1/2*I1*omega^2+m*g*l*cos(phi)

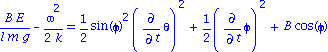
B*E/(l*m*g)-1/2*omega^2/k = 1/2*sin(phi)^2*diff(theta, t)^2+1/2*diff(phi, t)^2+B*cos(phi)

3ieme Integrale premiere (après simplification)

> B*u0=lhs(IP3);rel4:=%:
B*u0=rhs(IP3);IP3a:=%:

B*u0 = B*E/(l*m*g)-1/2*omega^2/k

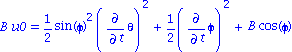
B*u0 = 1/2*sin(phi)^2*diff(theta, t)^2+1/2*diff(phi, t)^2+B*cos(phi)

3 integrales premieres du mouvement

> IP1;IP2;IP3a;

diff(psi, t)+cos(phi)*diff(theta, t) = omega

diff(theta, t) = -omega*(-k0+cos(phi)*k)/sin(phi)^2

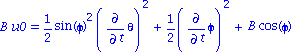
B*u0 = 1/2*sin(phi)^2*diff(theta, t)^2+1/2*diff(phi, t)^2+B*cos(phi)

>

Etude d'une toupie: disque de rayon R  sur un axe de longueur l=2R

> l:=2*R;

l := 2*R

> I1:=1/2*m*R^2; I20:=m*R^2+m*l^2; k:=I20/I1; B:=l*m*g/I20;

I1 := 1/2*m*R^2

I20 := 5*m*R^2

k := 10

B := 2/5*g/R

Verification avec le mouvement simple de precession dans le cas phi=Pi/2

> phi=Pi/2; rel:=%:

phi = 1/2*Pi

> #eq1a; eq2a; eq3a;

Report dans les 3 equations du mouvement

> subs(phi=Pi/2,eq1a):eval(%);
subs(phi=Pi/2,eq2a):eval(%);diff(theta,t)=solve(%,diff(theta,t));
subs(phi=Pi/2,eq3a):eval(%);

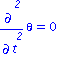
diff(theta, `$`(t, 2)) = 0

0 = -1/10*diff(theta, t)*omega+2/5*g/R

diff(theta, t) = 4*g/(omega*R)

diff(psi, t) = omega

Solution triviale (g=10, omega=100, R=0.1)

> Theta1:=t->4*t; Phi1:=t->Pi/2; Psi1:=t->100*t;

Theta1 := proc (t) options operator, arrow; 4*t end proc

Phi1 := proc (t) options operator, arrow; 1/2*Pi end proc

Psi1 := proc (t) options operator, arrow; 100*t end proc

Mouvement de la toupie

> T:=2; N:=50; dT:=T/N;
for i from 1 to N do
 T:=evalf(i*dT);
 anim[i]:=Toupie(Theta1(T),Phi1(T)):
end do:
display([seq(anim[i],i=1..N)],insequence=true,scaling=constrained,orientation=[50,74],axes=BOXED);

T := 2

N := 50

dT := 1/25

[Plot]

Trace de la trajectoire d'un point de l'axe

> OG1:=vector([cos(Theta1(t))*sin(Phi1(t)),sin(Theta1(t))*sin(Phi1(t)),cos(Phi1(t))]);
sph := sphere([0,0,0], 0.99):
traj:=spacecurve(OG1,t=0..2,color=black,thickness=4):

OG1 := vector([cos(4*t), sin(4*t), 0])

> display({sph,traj},scaling=constrained, style=patchnogrid, axes=boxed,title="Trajectoire de G (precession)");

[Plot]

Détermination de la solution dans le cas général

Parametres

> R:=1/10; g:=10; Theta:='Theta': Phi:='Phi':

R := 1/10

g := 10

Equations

> subs(theta=Theta(t),phi=Phi(t),eq1a); edp1:=%:
subs(theta=Theta(t),phi=Phi(t),eq2a); edp2:=%:
subs(phi=Phi(t),eq3a);

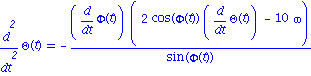
diff(Theta(t), `$`(t, 2)) = -diff(Phi(t), t)*(2*cos(Phi(t))*diff(Theta(t), t)-10*omega)/sin(Phi(t))

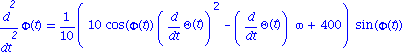
diff(Phi(t), `$`(t, 2)) = 1/10*(10*cos(Phi(t))*diff(Theta(t), t)^2-diff(Theta(t), t)*omega+400)*sin(Phi(t))

diff(psi, t)+cos(Phi(t))*diff(theta, t) = omega

Conditions initiales

> Theta(0)=0,D(Theta)(0)=1.0,Phi(0)=Pi/3,D(Phi)(0)=0;CI:=%:

Theta(0) = 0, D(Theta)(0) = 1.0, Phi(0) = 1/3*Pi, D(Phi)(0) = 0

très grande vitesse de rotation de la toupie: omega très grand

> omega:=100; Tmax:=1/2; edp1,edp2;

omega := 100

Tmax := 1/2

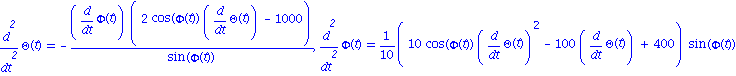
diff(Theta(t), `$`(t, 2)) = -diff(Phi(t), t)*(2*cos(Phi(t))*diff(Theta(t), t)-1000)/sin(Phi(t)), diff(Phi(t), `$`(t, 2)) = 1/10*(10*cos(Phi(t))*diff(Theta(t), t)^2-100*diff(Theta(t), t)+400)*sin(Phi(t...

Resolution

> dsol:=dsolve({edp1,edp2,CI},numeric,output=listprocedure);

dsol := [t = proc (t) local res, data, solnproc; option `Copyright (c) 1993 by the University of Waterloo. All rights reserved.`; data := module () local Data; export Get, Set; end module; solnproc :=...

> Phi1:=rhs(dsol[2]);Theta1:=rhs(dsol[4]);
dPhi1:=rhs(dsol[3]);dTheta1:=rhs(dsol[5]);

Phi1 := proc (t)::; local res, data, solnproc, outpoint, Phi(t); option `Copyright (c) 2000 by Waterloo Maple Inc. All rights reserved.`; _EnvDSNumericSaveDigits := Digits; Digits := 15; if _EnvInFsol...

Theta1 := proc (t)::; local res, data, solnproc, outpoint, Theta(t); option `Copyright (c) 2000 by Waterloo Maple Inc. All rights reserved.`; _EnvDSNumericSaveDigits := Digits; Digits := 15; if _EnvIn...

dPhi1 := proc (t)::; local res, data, solnproc, outpoint, diff(Phi(t),t); option `Copyright (c) 2000 by Waterloo Maple Inc. All rights reserved.`; _EnvDSNumericSaveDigits := Digits; Digits := 15; if _...

dTheta1 := proc (t)::; local res, data, solnproc, outpoint, diff(Theta(t),t); option `Copyright (c) 2000 by Waterloo Maple Inc. All rights reserved.`; _EnvDSNumericSaveDigits := Digits; Digits := 15; ...

> plot(Phi1(t),t=0..Tmax,title="nutation tres faible / omega tres grand");

[Plot]

> plot([dTheta1(t),dPhi1(t),omega-cos(Phi1(t))*dTheta1(t)],t=0..Tmax,legend=["dTheta","dPhi","dPsi"],title="Vitesse angulaire");

[Plot]

>

Trace de la trajectoire d'un point de l'axe

> OG1:=vector([cos(Theta1(t))*sin(Phi1(t)),sin(Theta1(t))*sin(Phi1(t)),cos(Phi1(t))]);
sph := sphere([0,0,0], 0.9):
traj:=spacecurve(OG1,t=0..2*Tmax,color=black,thickness=4,numpoints=200):

OG1 := vector([cos(Theta1(t))*sin(Phi1(t)), sin(Theta1(t))*sin(Phi1(t)), cos(Phi1(t))])

> display({sph,traj},scaling=constrained, style=patchnogrid, axes=boxed,title="Trajectoire de G");

[Plot]

>

On retrouve le mouvement de précésion

grande vitesse de rotation de la toupie: omega grand

> omega:=50; Tmax:=1; edp1,edp2;

omega := 50

Tmax := 1

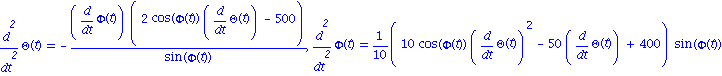
diff(Theta(t), `$`(t, 2)) = -diff(Phi(t), t)*(2*cos(Phi(t))*diff(Theta(t), t)-500)/sin(Phi(t)), diff(Phi(t), `$`(t, 2)) = 1/10*(10*cos(Phi(t))*diff(Theta(t), t)^2-50*diff(Theta(t), t)+400)*sin(Phi(t))

Resolution

> dsol:=dsolve({edp1,edp2,CI},numeric,output=listprocedure);

dsol := [t = proc (t) local res, data, solnproc; option `Copyright (c) 1993 by the University of Waterloo. All rights reserved.`; data := module () local Data; export Get, Set; end module; solnproc :=...

> Phi1:=rhs(dsol[2]);Theta1:=rhs(dsol[4]);
dPhi1:=rhs(dsol[3]);dTheta1:=rhs(dsol[5]);

Phi1 := proc (t)::; local res, data, solnproc, outpoint, Phi(t); option `Copyright (c) 2000 by Waterloo Maple Inc. All rights reserved.`; _EnvDSNumericSaveDigits := Digits; Digits := 15; if _EnvInFsol...

Theta1 := proc (t)::; local res, data, solnproc, outpoint, Theta(t); option `Copyright (c) 2000 by Waterloo Maple Inc. All rights reserved.`; _EnvDSNumericSaveDigits := Digits; Digits := 15; if _EnvIn...

dPhi1 := proc (t)::; local res, data, solnproc, outpoint, diff(Phi(t),t); option `Copyright (c) 2000 by Waterloo Maple Inc. All rights reserved.`; _EnvDSNumericSaveDigits := Digits; Digits := 15; if _...

dTheta1 := proc (t)::; local res, data, solnproc, outpoint, diff(Theta(t),t); option `Copyright (c) 2000 by Waterloo Maple Inc. All rights reserved.`; _EnvDSNumericSaveDigits := Digits; Digits := 15; ...

> plot(Phi1(t),t=0..1,title="apparition de feston de nutation");

[Plot]

> plot([dTheta1(t),dPhi1(t),omega-cos(Phi1(t))*dTheta1(t)],t=0..Tmax,legend=["dTheta","dPhi","dPsi"],title="Vitesse angulaire");

[Plot]

> OG1:=vector([cos(Theta1(t))*sin(Phi1(t)),sin(Theta1(t))*sin(Phi1(t)),cos(Phi1(t))]);
sph := sphere([0,0,0], 0.95):
traj:=spacecurve(OG1,t=0..Tmax/2,color=black,thickness=4,numpoints=400):

OG1 := vector([cos(Theta1(t))*sin(Phi1(t)), sin(Theta1(t))*sin(Phi1(t)), cos(Phi1(t))])

> display({sph,traj},scaling=constrained, style=patchnogrid, axes=boxed,title="Trajectoire de G");

[Plot]

>

cas omega petit

> omega:=10; Tmax:=1; edp1,edp2;

omega := 10

Tmax := 1

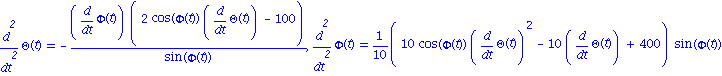
diff(Theta(t), `$`(t, 2)) = -diff(Phi(t), t)*(2*cos(Phi(t))*diff(Theta(t), t)-100)/sin(Phi(t)), diff(Phi(t), `$`(t, 2)) = 1/10*(10*cos(Phi(t))*diff(Theta(t), t)^2-10*diff(Theta(t), t)+400)*sin(Phi(t))

Resolution

> dsol:=dsolve({edp1,edp2,CI},numeric,output=listprocedure);

dsol := [t = proc (t) local res, data, solnproc; option `Copyright (c) 1993 by the University of Waterloo. All rights reserved.`; data := module () local Data; export Get, Set; end module; solnproc :=...

> Phi1:=rhs(dsol[2]);Theta1:=rhs(dsol[4]);
dPhi1:=rhs(dsol[3]);dTheta1:=rhs(dsol[5]);

Phi1 := proc (t)::; local res, data, solnproc, outpoint, Phi(t); option `Copyright (c) 2000 by Waterloo Maple Inc. All rights reserved.`; _EnvDSNumericSaveDigits := Digits; Digits := 15; if _EnvInFsol...

Theta1 := proc (t)::; local res, data, solnproc, outpoint, Theta(t); option `Copyright (c) 2000 by Waterloo Maple Inc. All rights reserved.`; _EnvDSNumericSaveDigits := Digits; Digits := 15; if _EnvIn...

dPhi1 := proc (t)::; local res, data, solnproc, outpoint, diff(Phi(t),t); option `Copyright (c) 2000 by Waterloo Maple Inc. All rights reserved.`; _EnvDSNumericSaveDigits := Digits; Digits := 15; if _...

dTheta1 := proc (t)::; local res, data, solnproc, outpoint, diff(Theta(t),t); option `Copyright (c) 2000 by Waterloo Maple Inc. All rights reserved.`; _EnvDSNumericSaveDigits := Digits; Digits := 15; ...

> plot(Phi1(t),t=0..1,title="apparition de feston de nutation omega grand");

[Plot]

> plot([dTheta1(t),dPhi1(t),omega-cos(Phi1(t))*dTheta1(t)],t=0..Tmax,legend=["dTheta","dPhi","dPsi"],title="Vitesse angulaire");

[Plot]

> OG1:=vector([cos(Theta1(t))*sin(Phi1(t)),sin(Theta1(t))*sin(Phi1(t)),cos(Phi1(t))]);
sph := sphere([0,0,0], 0.95):
traj:=spacecurve(OG1,t=0..Tmax,color=black,thickness=4,numpoints=400):

OG1 := vector([cos(Theta1(t))*sin(Phi1(t)), sin(Theta1(t))*sin(Phi1(t)), cos(Phi1(t))])

> display({sph,traj},scaling=constrained, style=patchnogrid, axes=boxed,title="Trajectoire de G");

[Plot]

>

cas omega tres petit

> omega:=1; Tmax:=1; edp1,edp2;

omega := 1

Tmax := 1

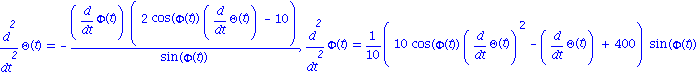
diff(Theta(t), `$`(t, 2)) = -diff(Phi(t), t)*(2*cos(Phi(t))*diff(Theta(t), t)-10)/sin(Phi(t)), diff(Phi(t), `$`(t, 2)) = 1/10*(10*cos(Phi(t))*diff(Theta(t), t)^2-diff(Theta(t), t)+400)*sin(Phi(t))

Resolution

> dsol:=dsolve({edp1,edp2,CI},numeric,output=listprocedure);

dsol := [t = proc (t) local res, data, solnproc; option `Copyright (c) 1993 by the University of Waterloo. All rights reserved.`; data := module () local Data; export Get, Set; end module; solnproc :=...

> Phi1:=rhs(dsol[2]);Theta1:=rhs(dsol[4]);
dPhi1:=rhs(dsol[3]);dTheta1:=rhs(dsol[5]);

Phi1 := proc (t)::; local res, data, solnproc, outpoint, Phi(t); option `Copyright (c) 2000 by Waterloo Maple Inc. All rights reserved.`; _EnvDSNumericSaveDigits := Digits; Digits := 15; if _EnvInFsol...

Theta1 := proc (t)::; local res, data, solnproc, outpoint, Theta(t); option `Copyright (c) 2000 by Waterloo Maple Inc. All rights reserved.`; _EnvDSNumericSaveDigits := Digits; Digits := 15; if _EnvIn...

dPhi1 := proc (t)::; local res, data, solnproc, outpoint, diff(Phi(t),t); option `Copyright (c) 2000 by Waterloo Maple Inc. All rights reserved.`; _EnvDSNumericSaveDigits := Digits; Digits := 15; if _...

dTheta1 := proc (t)::; local res, data, solnproc, outpoint, diff(Theta(t),t); option `Copyright (c) 2000 by Waterloo Maple Inc. All rights reserved.`; _EnvDSNumericSaveDigits := Digits; Digits := 15; ...

> plot(Phi1(t),t=0..1,title="apparition de feston de nutation omega grand");

[Plot]

> plot([dTheta1(t),dPhi1(t),omega-cos(Phi1(t))*dTheta1(t)],t=0..Tmax,legend=["dTheta","dPhi","dPsi"],title="Vitesse angulaire");

[Plot]

> OG1:=vector([cos(Theta1(t))*sin(Phi1(t)),sin(Theta1(t))*sin(Phi1(t)),cos(Phi1(t))]);
sph := sphere([0,0,0], 0.95):
traj:=spacecurve(OG1,t=0..4*Tmax,color=black,thickness=4,numpoints=400):

OG1 := vector([cos(Theta1(t))*sin(Phi1(t)), sin(Theta1(t))*sin(Phi1(t)), cos(Phi1(t))])

> display({sph,traj},scaling=constrained, style=patchnogrid, axes=boxed,title="Trajectoire de G");

[Plot]

>

Omega très très petit (mouvement du pendule 3D)

> omega:=0.01;Tmax:=1; edp1,edp2;

omega := 0.1e-1

Tmax := 1

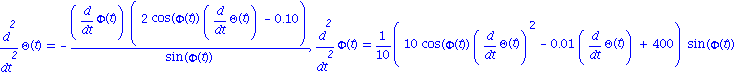
diff(Theta(t), `$`(t, 2)) = -diff(Phi(t), t)*(2*cos(Phi(t))*diff(Theta(t), t)-.10)/sin(Phi(t)), diff(Phi(t), `$`(t, 2)) = 1/10*(10*cos(Phi(t))*diff(Theta(t), t)^2-0.1e-1*diff(Theta(t), t)+400)*sin(Phi...

Resolution

> dsol:=dsolve({edp1,edp2,CI},numeric,output=listprocedure);

dsol := [t = proc (t) local res, data, solnproc; option `Copyright (c) 1993 by the University of Waterloo. All rights reserved.`; data := module () local Data; export Get, Set; end module; solnproc :=...

> Phi1:=rhs(dsol[2]);Theta1:=rhs(dsol[4]);
dPhi1:=rhs(dsol[3]);dTheta1:=rhs(dsol[5]);

Phi1 := proc (t)::; local res, data, solnproc, outpoint, Phi(t); option `Copyright (c) 2000 by Waterloo Maple Inc. All rights reserved.`; _EnvDSNumericSaveDigits := Digits; Digits := 15; if _EnvInFsol...

Theta1 := proc (t)::; local res, data, solnproc, outpoint, Theta(t); option `Copyright (c) 2000 by Waterloo Maple Inc. All rights reserved.`; _EnvDSNumericSaveDigits := Digits; Digits := 15; if _EnvIn...

dPhi1 := proc (t)::; local res, data, solnproc, outpoint, diff(Phi(t),t); option `Copyright (c) 2000 by Waterloo Maple Inc. All rights reserved.`; _EnvDSNumericSaveDigits := Digits; Digits := 15; if _...

dTheta1 := proc (t)::; local res, data, solnproc, outpoint, diff(Theta(t),t); option `Copyright (c) 2000 by Waterloo Maple Inc. All rights reserved.`; _EnvDSNumericSaveDigits := Digits; Digits := 15; ...

> plot(Phi1(t),t=0..1,title="apparition de feston de nutation omega grand");

[Plot]

> plot([dTheta1(t),dPhi1(t),omega-cos(Phi1(t))*dTheta1(t)],t=0..Tmax,legend=["dTheta","dPhi","dPsi"],title="Vitesse angulaire");

[Plot]

> OG1:=vector([cos(Theta1(t))*sin(Phi1(t)),sin(Theta1(t))*sin(Phi1(t)),cos(Phi1(t))]);
sph := sphere([0,0,0], 0.95):
traj:=spacecurve(OG1,t=0..5*Tmax,color=black,thickness=4,numpoints=400):

OG1 := vector([cos(Theta1(t))*sin(Phi1(t)), sin(Theta1(t))*sin(Phi1(t)), cos(Phi1(t))])

> display({sph,traj},scaling=constrained, style=patchnogrid, axes=boxed,title="Trajectoire de G");

[Plot]

FIN !