%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
plt.rc('font', family='serif', size='16')
from IPython.display import display, HTML, YouTubeVideo, Video, IFrame
YouTubeVideo('yVkdfJ9PkRQ',width=800,height=600)
L'objectif de cette étude est de construire un modèle explicatif du mouvement de pendules dansants (swinging pendulum). Une expérience illustrant cette danse des pendules a été réalisée pour un cours d'introduction à la physique: Harward Natural Sciences Lectures by Tom Fuller
Quinze pendules simples non couplés de longueurs monotones croissantes dansent ensemble pour produire des ondes visuelles progressives, des ondes stationnaires, des battements et (apparemment) des mouvements aléatoires.
vidéo youtube avec de la musique fonction du mouvement
Video courtesy of Harvard Natural Sciences Lecture Demonstrations, © 2010 President and Fellows of Harvard College
Pour construire un modèle, nous allons tout d'abord étudier le mouvement du pendule simple, en utilisant les possibilités de visualisation des notebooks Python.
Puis nous nous intéresserons au mouvement de 2 pendules de longueurs différentes pour ensuite passer au cas d'une série de 15 pendules de longueurs croissantes permettant de retrouver les mouvements observés dans la vidéo.
On considère un pendule simple, constitué d'une masse $m$ fixée à l’extrémité d'un fil de longueur $l_1$ fixé en O et soumis à la gravité $g$.
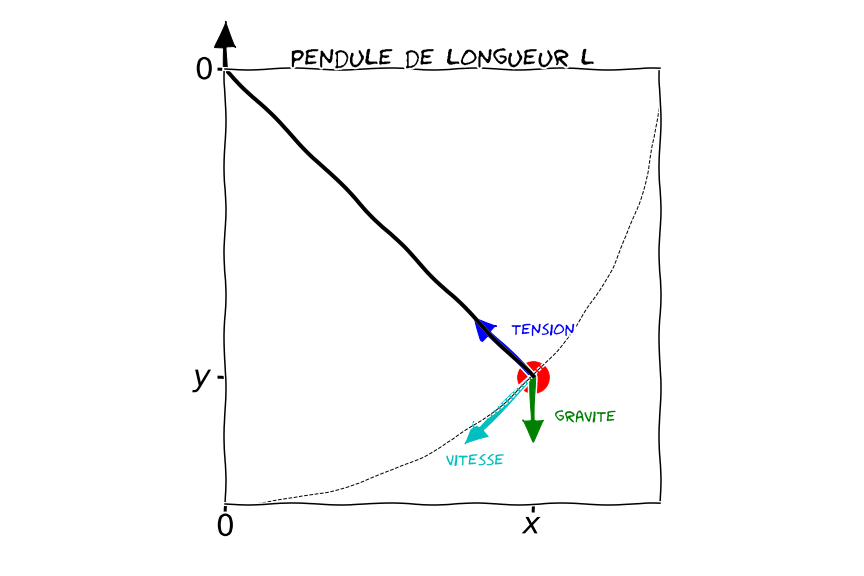
La position $P$ de la masse s'écrit en fonction de l'angle $\theta_1$ du fil par rapport à la verticale $y$:
$$ \overrightarrow{OP} = \left[\begin{array}{l}x_1\\y_1\end{array}\right] = \left[\begin{array}{l}+l_1\sin\theta_1\\-l_1\cos\theta_1\end{array}\right] $$
Soit $\overrightarrow{e_t}$ le vecteur tangentiel (dans la direction de la vitesse), et $\overrightarrow{e_n}$ le vecteur normal (dans la direction du fil), la vitesse du pendule s'écrit:
$$\overrightarrow{v}=l_1\frac{d\theta_1}{dt}\overrightarrow{e_t}$$
Les forces exercées sur le pendule sont la gravité $- m g \overrightarrow{e_y}$ suivant la verticale $\overrightarrow{e_y}$ et la tension dans le fil $T \overrightarrow{e_n}$ dans la direction du fil $\overrightarrow{e_n}$
Le principe fondamental de la dynamique (loi de Newton) s'écrit:
$$ \frac{d}{dt}(m l_1 \frac{d\theta_1}{dt}\overrightarrow{e_t})= -m g \overrightarrow{e_y} + T \overrightarrow{e_n} $$
En projetant cette équation dans la direction de la vitesse $\overrightarrow{e_t}$, on élimine la tension et on obtiens l'équation d'évolution de l'angle $\theta(t)$, sous la forme d'une équation différentielle du second ordre.
$$ m l_1 \frac{d^2\theta_1}{dt^2} = - m g \sin\theta_1 $$
Dans le cas de petites oscillations, l'angle $\theta_1$ reste petit et on peut approximer $\sin\theta_1 \approx \theta_1$ , ce qui permet de linéariser l'équation différentielle précédente:
$$ \frac{d^2\theta_1}{dt^2} = -\omega_1^2 \theta_1 \mbox{ avec } \omega_1=\sqrt{\frac{g}{l_1}}$$
dont le paramétre est la pulsation $\omega_1$.
solution
En supposant que le pendule est laché avec un angle $\theta_1(t=0)=\theta_0$ à l'instant initial sans vitesse initiale $\dot{\theta_1}(t=0)=0$, la solution de l'équation linéarisée est la solution classique du pendule simple:
$$\theta_1(t) = \theta_0\cos(\omega_1 t)$$
qui indique que le pendule oscille de façon périodique sinusoïdale avec une période $T_1$: $$T_1 = \frac{2\pi}{\omega_1} = 2 \pi \sqrt{\frac{l_1}{g}}$$
qui dépend donc de sa longueur $l_1$.
La tension dans le fil étant perpendiculaire à la vitesse, son travail est nul. La gravité découle d'un potentiel, et donc le système est conservatif.
L'énergie totale, somme de l'énergie cinétique et l'énergie potentiel de gravite, reste constante au cours du mouvement
$$ E_t = \frac{1}{2} m v_1^2 + m g y_1 = cste$$
on va calculer numériquement la solution en choisissant les valeurs numériques des paramètres et en traduisant les formules mathématiques en expressions python en utilisant des notations vectorielles de la bibliothéque numpy.
\begin{align} \theta_1(t) &= \theta_0\cos(\omega_1 t) \\ \dot{\theta_1}(t) &= -\omega_1\theta_0\sin(\omega_1 t) \end{align}
\begin{align} X_1 &= l_1 \sin(\theta_1)\\ Y_1 &= -l_1 \cos(\theta_1) \end{align}
$$ V_1 = l_1 \dot{\theta_1}$$
\begin{align} Ec &= 0.5 m_1 V_1^2 \\ Ep &= m_1 g Y_1 \end{align}
# definition des parametres
g = 10.0
l1 = 0.1
m1 = 1.0
theta0 = np.pi/8
omega1 = np.sqrt(g/l1)
# periode
T0 = 2*np.pi/omega1
# temps de simulation
M = 5
tf = M*T0
# solution
TT = np.linspace(0,tf,50*M+1)
THETA1 = theta0*np.cos(omega1*TT)
plt.figure(figsize=(10,6))
plt.plot(TT,THETA1)
plt.title("solution pendule simple")
plt.xlabel("t en s.")
plt.ylabel("$\\theta_1(t)$ en radian");
X1 = l1*np.sin(THETA1)
Y1 = -l1*np.cos(THETA1)
plt.figure(figsize=(10,6))
plt.plot(X1,Y1)
plt.title("Trajectoire")
plt.xlabel("X1 en m")
plt.ylabel("Y1 en m")
plt.axis('equal');
# calcul energie
V1 = -l1*omega1*theta0*np.sin(omega1*TT)
Ec = 0.5*m1*V1**2
Ep = m1*g*Y1
plt.figure(figsize=(10,6))
plt.plot(TT,Ec,label="Ec")
plt.plot(TT,Ep,label="Ep")
plt.plot(TT,Ec+Ep,'--',label="Ec+Ep")
plt.title("Variation d'énergie")
plt.xlabel('t en s.')
plt.legend();
L'animation suivante montre l'évolution du vecteur vitesse (en cyan) et accélération (en vert)
Video("pendulum.mp4",embed=True,width=640,height=480)
En prenant 2 pendules de longueurs $l_1$ et $l_2$, accrochés à une même barre et lachés avec le même angle $\theta_0$.
Les angles de rotations $\theta_1(t)$ et $\theta_2(t)$ sont donnés par:
$$ \theta_1(t) = \theta_0 \cos{\sqrt{\frac{g}{l_1} t }} $$ $$ \theta_2(t) = \theta_0 \cos{\sqrt{\frac{g}{l_2} t }} $$
Si on choisit bien les longueurs $l_1$ et $l_2$ , on peut avoir des mouvements en phase ou en opposition de phase avec une période commune. Pour cela il faut que les périodes des 2 pendules soient dans un rapport rationnel: $$ \frac{T_1}{T_2} = \frac{m}{p} \mbox{ avec } m,p \in \mathbb{N^+}$$
ce qui impose le rapport des longueurs. On choisit par exemple: $$ \frac{l_2}{l_1} = \frac{m^2}{(m-1)^2} \mbox{ avec } m=20 $$
Si on part du même angle $\theta_0$ à $t=0$, alors au bout d'un temps $t_f = m T_2$ les 2 pendules se retrouvent à la mếme position $\theta_0$.
C'est ce que l'on va vérifier en traçant les différentes trajectoires des deux pendules
# parametres
M = 20
l2 = l1*M**2/(M-1)**2
omega2 = np.sqrt(g/l2)
# solution
T0 = 2*np.pi/omega2
tf = M*T0
TT = np.linspace(0,tf,50*M+1)
THETA1 = theta0*np.cos(omega1*TT)
THETA2 = theta0*np.cos(omega2*TT)
plt.figure(figsize=(10,6))
plt.plot(TT,THETA1,label="$\\theta_1$")
plt.plot(TT,THETA2,label="$\\theta_2$")
plt.legend()
plt.title("solution pendule simple")
plt.xlabel("t en s.")
plt.ylabel("$\\theta(t)$ en radian");
#plt.savefig("pendule2.png")
plt.figure(figsize=(10,6))
plt.plot(THETA1,THETA2)
plt.xlabel("$\\theta_1(t)$ en radian")
plt.ylabel("$\\theta_2(t)$ en radian")
plt.title("Courbe de Lissajoux");
#plt.savefig("lissajoux.png")
L'animation suivante montre la trajectoire des pendules
Video("swing_pendulum2.mp4",embed=True,width=640,height=480)
On considère N pendules simples de longueur $l_i$ accrochés sur une même barre. A l'instant initiale, on les lâche avec le même angle $\theta_0$. Leur mouvement $\theta_i(t)$ , en petites oscillations, est donné par l'équation $$\theta_i(t) = \theta_0 \cos{\sqrt{\frac{g}{l_i} t }} $$
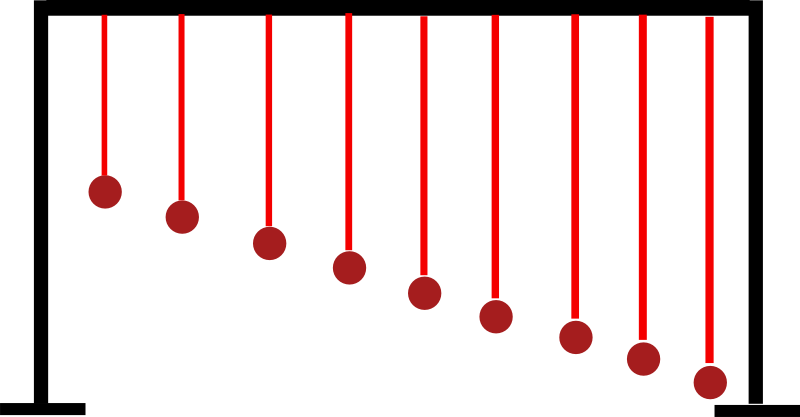
En choisissant les longueurs $l_i$ telle que s
$$ l_i = l_0 \frac{ M^2}{(M-i)^2} \mbox{ avec } M > N$$
les pendules vont se retrouver en phase au bout de $M$ périodes du plus grand $l$. En effet leurs périodes sont dans un rapport rationnel du type $\frac{M}{M-i}$
Leur mouvement d'ensemble ressemble alors à une propagation d'ondes, d'où le nom "swinging pendulum"
L'animation suivante montre la trajectoire des pendules. Les quinze pendules simples non couplés de longueurs monotones croissantes dansent ensemble pour produire des ondes visuelles progressives, des ondes stationnaires, des battements et (apparemment) des mouvements aléatoires de la même façon que sur la vidéo de l'expérience.
Video("swing_pendulum.mp4",embed=True,width=640,height=480)
A l'aide d'une expérience numérique utilisant des notebooks Jupyter, un peu de code Python et des visualisations de simulation numérique, on a pu expliquer la danse des pendules observée sur la vidéo de l'expérience initiale. On a ainsi montré que
vidéo utilisant ce notebook en mode présentation avec des sous-titres
version initiale de la danse des pendules avec sous titre (media-center Lyon1)
version youtube
IFrame('https://myvideo.univ-lyon1.fr/permalink/v126648a9a047xeg3hk0/iframe/#start=1',width='640',height='480')
YouTubeVideo('KdWZLV7RfkE',width=640,height=400)