4.9 Fonction

Pour définir une nouvelle fonction sous Matlab, on écrit la définition de la fonction dans un fichier avec une extension .m (fonction M-File). Le nom du fichier doit être le nom de la première fonction définie (la seule visible). On l'exécute en tapant le nom de la fonction avec entre parenthèses la liste des arguments.

La première ligne du fichier de la fonction doit suivre la syntaxe suivante:

syntaxe:

function arguments de sortie = nom(arguments d'entrée)

On doit donc déclarer les valeurs calculées par la fonction dans les arguments de sortie, et les paramètres de la fonction dans les arguments d'entrée (qui ne sont pas modifiés).

Attention, contrairement au script, les variables d'une fonction sont des variables locales, qui ne sont pas accessibles en dehors de la fonction. Pour passer des information à une fonction, il faut donc utiliser les paramètres d'entrée ou de sortie. En fait on peut utiliser des variables globales (mot clé global) sous Matlab, mais cela est à éviter dans le cadre d'une bonne programmation.

programme matlab 3.9: fonction récurcive calculant par dichotomie de la racine d'une fonction

function x=racine(a,b)
% calcul la racine de f(x) définie ci-après sur [a,b]
fa=f(a); fb=f(b); x=(a+b)/2;
if (fa*fb>0) x=-Inf; return; end;
while (b-a)>eps*x
  x=(a+b)/2; fx=f(x);
  if(sign(fx)==sign(fa))
   a=x; fa=fx;
  else
   b=x; fb=fx;
  end;
end;
% definition de f(x) (fonction locale)
function y=f(x)
y=x^3-2*x-5;

La fonction racine ci dessus est écrite dans un fichier racine.m. Pour l'exécuter, on tape simplement

>>racine(0,3)

$$ans=2.0946$$

On peut écrire des fonctions récursives, comme la fonction suivante qui calcule $n!$

programme matlab 3.9: fonction récurcive calculant n!

function y=fact(n)
if (n<=1) y=1
else y=n*fact(n-1)
end

mais en général, ces fonctions peuvent s'écrire plus efficacement avec des boucles

programme matlab 3.9: fonction calculant n!

function y=fact(n)
y=prod(1:n);

On peut aussi utiliser des pointeurs (ou adresses) vers une fonction pour permettre le passage de fonctions en argument. Sous Matlab, un pointeur vers une fonction est un handle.

function handle=$@$function

est le pointeur (adresse) vers la fonction function.

Pour évaluer un pointeur on utilise la fonction feval

syntaxe:

feval(handle,liste des arguments)

Dans l'exemple suivant, on calcule l'intégrale d'une fonction $f(x)$passée en argument à l'aide de la méthode des trapèzes:

$$\int_{a}^{b}\, f(x)dx\simeq\frac{h}{2}\left(f(a)+f(b)+2\sum_{i=1}^{n-1}f(x_{i})\right)$$

programme matlab 3.9: fonction calculant l'intégrale de f(x)

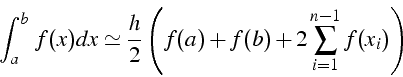
function A=trapezes(ptr_f,a,b,n)
h=(b-a)/n; 
X=[a:h:b]; 
Y=feval(ptr_f,X);
A=h*((Y(1)+Y(n+1))/2+sum(Y(2:n)));

Un exemple d'utilisation pour calculer numériquement $\int_{0}^{\pi}sin(x)\, dx$ s'écrit

>>fp=@sin

>>trapezes(fp,0,pi/2,100)

$ans\,=\,1.0000$