La vectorisation

Vous allez apprendre à tirer le meilleur parti de Python associé avec numpy en utilisant des fonctions préprogrammées qui traitent les vecteurs ou les matrices globalement. C’est ce que l’on appelle la "vectorisation".

Rappel sur les extractions d'élements :

Je crée une matrice C 4x5 qui est la matrice de VanderMonde, il existe une fonction toute faite pour cela dans numpy. Le détail de la matrice importe peu pour ce cours (plus d'informations sur cette matrice dans votre cours de mathématiques ou bien sur wikipedia)

In [2]:
import numpy as np

C = np.vander([1,2,3,5], 5,increasing=True)
print(C)

[[  1   1   1   1   1]
 [  1   2   4   8  16]
 [  1   3   9  27  81]
 [  1   5  25 125 625]]

On peut extraire une sous-matrice de C en utilisant les deux points ":" comme nous l'avons déjà vu lors de l'introduction à Numpy. Il est aussi possible d'imposer le pas avec la syntaxe debut:fin:pas exemple 2:11:2 prendra les éléments entre le "piquet" 2 et le "piquet" 11 avec un pas de 2.

In [3]:
print("Extraction de C \n",C[0:3,1:3])  # Extrait entre le piquet 0 et le piquet 3 pour le premier indice 
                                        # et du piquet 1 au piquet 3 pour le deuxième indice. 
# ce qui correspond aux lignes 1, 2 et 3 et aux colonnes 2 et 3 de la matrice

print('Lignes et colonnes paires :\n',C[0:4:2,0:5:2]) # On impose un pas de 2

Extraction de C 
 [[1 1]
 [2 4]
 [3 9]]
Lignes et colonnes paires :
 [[ 1  1  1]
 [ 1  9 81]]

Il est aussi utile de se servir de -1, -2, -3, ... comme indices pour compter à partir de l'indice de fin du tableau. On peut aussi ne rien mettre pour désigner le début ou la fin.

In [50]:
print(C[1:-1,:]) # Extrait du deuxième à l'avant dernier élément pour le premier indice (les lignes) "1:-1" 
                 # et tous les éléments pour le deuxième indice (les colonnes)  avec ":"  

[[ 1  2  4  8 16]
 [ 1  3  9 27 81]]
In [51]:
C[:-2,1:]  # On part de 0 et on s'arrète à -2 de la fin pour le premier indice 
           # et on part de 1 jusqu'à la fin pour le deuxième indice.
Out[51]:
array([[ 1,  1,  1,  1],
       [ 2,  4,  8, 16]])

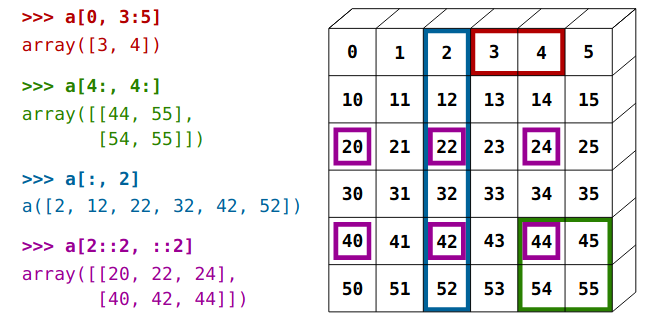
Ce schéma extrait des lectures notes de Scipy illustre bien les diverses possibilités:

Slicing en image

Tableaux : dimensions, notion d'axe, taille, nombre d'éléments

La fonction np.ndim permet de connaitre le nombre de dimensions du tableau. 1 pour un vecteur, 2 pour une matrice.

In [52]:
print("Nb de dimensions de C : ", np.ndim(C)) 

Nb de dimensions de C :  2

On introduit maintenant la notion d'axe de la matrice. L'axe 0 désigne la direction suivant le premier indice (de haut en bas), l'axe 1 la direction en faisant varier le deuxième indice (de gauche à droite).

A l'aide de la fonction np.size, il est possible d'obtenir le nombre total d'éléments d'une matrice, ou le nombre d'élements suivant un des axes.

In [53]:
print("Nb total d'éléments : ", np.size(C)) 
print("Nb d'éléments suivant l'axe 0 : ", np.size(C,axis=0)) 
print("Nb d'éléments suivant l'axe 1 : ", np.size(C,1))  # On peut omettre le 'axis =' 

Nb total d'éléments :  20
Nb d'éléments suivant l'axe 0 :  4
Nb d'éléments suivant l'axe 1 :  5

A l'aide de la fonction np.shape, il est possible d'obtenir le nombre d'éléments dans chaque dimension d'un tableau. Par abus de langage, on va dire que l'on obtient les dimensions du tableau. np.shape renvoie un tuple.

In [55]:
print("Les dimensions du tableau C sont : ", np.shape(C)) 
print("C'est aussi équivalent d'utiliser la syntaxe : ", C.shape  )

Les dimensions du tableau C sont :  (4, 5)
C'est aussi équivalent d'utiliser la syntaxe :  (4, 5)

Manipulations de matrices.

Il existe dans numpy de nombreuses fonctions qui manipulent les tableaux. Il y a des fonctions inspirées des mathématiques comme la transposée mais aussi des fonctions comme rot90, flipud, fliplr (ud: veut dire Upside Down, lr: Left Right).

Pour plus d'information sur une fonction faire help(fonction). Par exemple help(np.rot90)

In [8]:
np.transpose(C)   # qui peut aussi s'écrire C.transpose()  ou en raccourci C.T
Out[8]:
array([[  1,   1,   1,   1],
       [  1,   2,   3,   5],
       [  1,   4,   9,  25],
       [  1,   8,  27, 125],
       [  1,  16,  81, 625]])
In [9]:
np.flipud(C)  # ou encore np.flip(C,axis=0) ou en raccourci np.flip(C,0) 0 désigne 
              # l'axe à choisir pour le flip
Out[9]:
array([[  1,   5,  25, 125, 625],
       [  1,   3,   9,  27,  81],
       [  1,   2,   4,   8,  16],
       [  1,   1,   1,   1,   1]])
In [10]:
np.fliplr(C) # ou encore np.flip(C,1)  ou np.flip(C,axis=1)
Out[10]:
array([[  1,   1,   1,   1,   1],
       [ 16,   8,   4,   2,   1],
       [ 81,  27,   9,   3,   1],
       [625, 125,  25,   5,   1]])
In [11]:
np.rot90(C) # tourne la matrice de 90 degrés dans le sens trigo.
Out[11]:
array([[  1,  16,  81, 625],
       [  1,   8,  27, 125],
       [  1,   4,   9,  25],
       [  1,   2,   3,   5],
       [  1,   1,   1,   1]])

Il est possible de réorganiser les éléments de la matrices avec la fonction np.reshape. Bien évidement le nombre d'éléments doit être égal au produit du nombre d'éléments dans chaque dimension (il y a 20 éléments dans notre exemple pour C on ne peut donc faire que (1,20) ou (2,10) ou (4,5) ou (5,4) ou (10,2) ou (20,1)... ).

In [12]:
print("C= \n",C)
print("C en matrice avec 10 lignes et 2 colonnes :\n", np.reshape(C,(10,2)))

C= 
 [[  1   1   1   1   1]
 [  1   2   4   8  16]
 [  1   3   9  27  81]
 [  1   5  25 125 625]]
C en matrice avec 10 lignes et 2 colonnes :
 [[  1   1]
 [  1   1]
 [  1   1]
 [  2   4]
 [  8  16]
 [  1   3]
 [  9  27]
 [ 81   1]
 [  5  25]
 [125 625]]

Fonctions préprogrammées, opérations simples

Dans numpy, en plus de la fonction np.zeros qui permet de créer un tableau de zéros, il existe son équivalent avec 1 np.ones. Deux autres fonctions peuvent être pratiques en algèbre linéaire np.eye et np.diag

In [13]:
print(" Matrice 3x3 de 1 \n",np.ones((3,3))) # Notez l'utilisation du tuple (3,3)
print(" Matrice identité 3x3 \n",np.eye(3))  # 3 est l'argument
print(" Matrice diagonale \n",np.diag([3.,4.,-1.,6.]))  # le vecteur diagonal est l'argument 
                                                        # la dimension de la matrice (carrée) s'adapte

 Matrice 3x3 de 1 
 [[1. 1. 1.]
 [1. 1. 1.]
 [1. 1. 1.]]
 Matrice identité 3x3 
 [[1. 0. 0.]
 [0. 1. 0.]
 [0. 0. 1.]]
 Matrice diagonale 
 [[ 3.  0.  0.  0.]
 [ 0.  4.  0.  0.]
 [ 0.  0. -1.  0.]
 [ 0.  0.  0.  6.]]

On crée deux matrices A et B afin de faire des opérations simples ou préprogrammées

  • A est une matrice nxn d'entiers allant de 1 à n² dont la somme des lignes, des colonnes et de la diagonale donnent la même valeur.
  • B est une matrice nxn d'entiers tirés aléatoirement entre 1 à n².

On prend ici n=3.

In [14]:
A = np.array([[8,1,6],[3,5,7],[4,9,2]]) 
B = np.random.randint(1,10, size=(3, 3))
print("A = \n",A)
print("B = \n",B)

A = 
 [[8 1 6]
 [3 5 7]
 [4 9 2]]
B = 
 [[6 8 4]
 [6 8 7]
 [7 4 1]]

Comme nous l'avons déjà vu, de manière assez intuitive et naturelle, on peut utiliser les opérateurs classiques d'addition, soustraction, division ou la multiplication entre A et B

In [15]:
A + B
Out[15]:
array([[14,  9, 10],
       [ 9, 13, 14],
       [11, 13,  3]])

donne bien le résultat prévu sachant que A et B sont conformants (ici les deux matrices sont de tailles 3x3). Derrière cette opération banale, il y a bien des boucles for qui sont réalisées de manière interne en parcourant chaque élément des tableaux. Ces opérations sont masquées et elles sont optimisées par python pour vous. En python, on évite autant que possible de coder soi même des boucles.

  • Il existe de nombreuses fonctions préprogrammées en numpy. Prenons par exemple np.sum que l'on a déjà vu pour un vecteur.
In [16]:
np.sum(A) # fait la somme de tous les éléments de A.
Out[16]:
45
In [17]:
np.sum(A,0) # renvoie un vecteur qui est la somme suivant l'axe 0 
            # c-à-d la somme de chaque colonne 8+3+4,1+5+9,6+7+2
Out[17]:
array([15, 15, 15])
In [18]:
np.sum(A,1) # renvoie un vecteur qui est la somme suivant l'axe 1 c-à-d la somme de chaque ligne
Out[18]:
array([15, 15, 15])
In [19]:
np.diag(A) # renvoie un vecteur contenant les éléments de la diagonale de A
Out[19]:
array([8, 5, 2])
In [20]:
np.sum(np.diag(A)) # enchainant les deux fonctions on obtient la somme des éléments de la diagonale de A
Out[20]:
15

Les fonctions np.min, np.max, np.mean (la moyenne) fonctionnent exactement sur le même principe que np.sum. Pour le max (ou le min), la fonction np.argmax (np.argmin) renvoie l'indice du max.