Le but de ce TP est d’apprendre à manipuler un film issu d'une expérience afin d’extraire des données en fonction du temps.

Ici on étudie l'oscillation d’un pendule, on comparera les données expérimentales avec une théorie simple.
Le but de ce TP est d’apprendre à manipuler un film issu d'une expérience afin d’extraire des données en fonction du temps.

Ici on étudie l'oscillation d’un pendule, on comparera les données expérimentales avec une théorie simple.
Vous avez vu durant les TP 4 et 5 que les images sont stockées sous la forme de matrices contenant la couleur (ou nuance de gris).
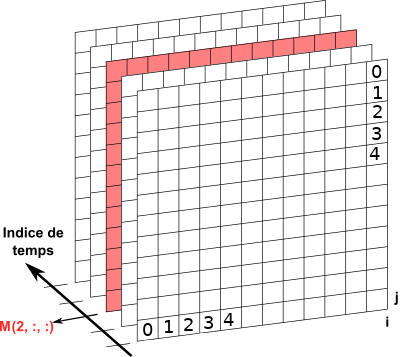
Un film étant une succession d’images dans le temps, il peut être stocké au moyen d’une matrice M(k,j,i) à 3 indices.
Les 2 derniers indices $(j,i)$ font référence à la position du pixel, comme dans une image classique. La dimension ($k$) correspond à l’indice de temps (et non à sa valeur).
La 3e image du film peut ainsi être appelée par la commande :
M[2,:,:]
Pour le tableau M(k,j,i) on a donc :
La figure suivante illustre ce stockage sous forme de matrice :
À partir des deux films (pendule court et pendule long), nous allons retrouver la relation existant entre la fréquence d’oscillation $T$ d’un pendule et sa longueur $L$, et la comparer avec la prédiction théorique pour de faibles oscillations : $$T=2\pi\sqrt{L/g}$$ où $g$ est l’accélération de la pesanteur. Les questions suivantes devront donc être réalisées sur les deux films de pendule (court et long) pour faire les comparaisons.Pour mettre au point commencez par faire tout le TP avec pendule court, il sera ensuite assez facile de généraliser.
La théorie veut que l’oscillation obtenue soit proche d’une oscillation sinusoïdale : $$ x(t)= \beta+\alpha \sin\left( \frac{2\pi t}{T} +\phi\right),$$ avec :
À partir du film, on souhaite obtenir l'évolution $x(t)$ puis mesurer la période $T$.
# On importe les modules nécessaires au TP
import imageio
import numpy as np
import matplotlib.pyplot as plt
import os
# Uniquement pour jupyter notebook
%matplotlib auto
Vous disposez de deux films (que vous pourrez prévisualiser en dehors de Python ...) avec une fréquence d'échantillonage de 100 images par seconde.
Pour vous faciliter la tâche, les films ont été convertis en tableaux et sauvegardés dans des fichiers .npy. Le script pour faire l'opération du passage d'un film .avi au fichier .npy est donné en annexe mais ce n'est pas au programme.
Les fichiers .npy sont des fichiers binaires. L'avantage des fichiers binaires est qu'ils sont très compacts (plus petits en espace de stockage). L'inconvénient est qu'ils ne peuvent pas être lus dans un éditeur et modifiés simplement. Pour les fichiers texte on a utilisé les commandes np.loadtxt et np.savetxt. Pour les fichiers binaires, on se sert des commandes np.load et np.save. L'esprit est le même.
L'instruction
tab_court = np.load('pendule_court.npy')
permet de charger le tableau tab_court correspondant aux "frames" de pendule_court.avi .
# Réponse
# Question 3
"""
On peut mettre les 2 tableaux dans une liste pour faire les 2 films dans une boucle sur la liste.
Pour la mise au point, mettre uniquement tab_court
"""
for tab in [tab_court, tab_long] :
nbrFrame = tab.shape[0] # Nombre de frames du film
kstart = 0
kstop = nbrFrame
kstep = 10
fig = plt.figure(figsize=(6,6))
ax = fig.gca()
h = ax.imshow(tab[0,::4, ::4], cmap='gray') # On ne représente qu'un pixel sur 4 avec la section de tableau ::4
for k in range(kstart, kstop, kstep) : # On parcourt le film de kstart à kstop par pas de kstep frames
h.set_data(tab[k, ::4, ::4])
plt.title('Image #'+str(k))
plt.draw()
plt.pause(1e-1)
# Réponse
# Réponse
plot
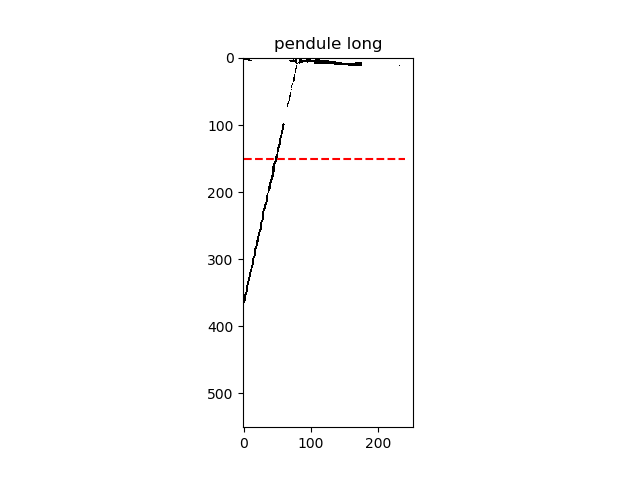
 Observez le résultat de la commande
Observez le résultat de la commande plt.imshow(np.transpose(tab_ligne), cmap='gray'), c'est un diagramme spatio temporel. On veut maintenant mettre des axes qui ne soient pas les indices du tableau. plt.pcolormesh(temps, dist, np.transpose(tab_ligne), cmap='gray') pour obtenir l'évolution spatio-temporelle ($x(t)$). plt.pcolormesh fonctionne comme plt.imshow en affichant l'image, mais permet en plus d'afficher des coordonnées en abscisses et en ordonnées autres que les indices.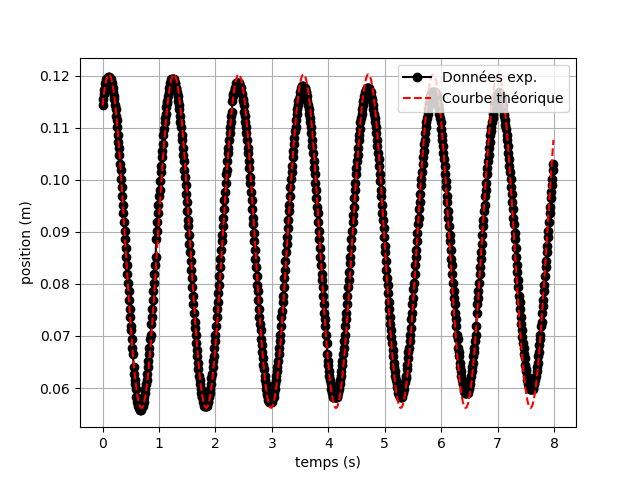
# Réponse
# Réponse
Dans ce TP, les deux fichiers .npy avec les tableaux contenant les images des deux films sont directement fournis au bon format pour Numpy. Dans la pratique, on dispose de films avec des formats classiques avi, mpeg, mp4 .... Ce qui suit vous explique comment relire vous-même ces films. Ce n’est pas au programme de l'UE.
Il faut tout d'abord installer un package supplémentaire imageio-ffmpeg qui n'est pas installé par défaut dans Anaconda. Pour faire cette installation, dans une fenêtre de Terminal (Linux ou mac OS) ou dans le terminal que l'on ouvre depuis Anaconda Navigator sous Windows, tapez la commande suivante:
conda install imageio-ffmpeg -c conda-forge
Vous aurez ainsi le package qui permet de relire les films dans divers formats.
Le script suivant fait l'opération souhaitée de conversion du film ici au format avi en fichier .npy.
import imageio
import numpy as np
fileAVI = ['pendule_long.avi', 'pendule_court.avi'] # fait la liste des films à relire
nameFinal = ['pendule_long', 'pendule_court'] # fait une liste des noms des fichiers de sauvegarde npy
for file, name in zip(fileAVI, nameFinal) : # On parcourt les deux listes grace à zip
reader = imageio.get_reader(file) # on associe à reader le film avi
frames = [] # crée la liste vide frames
for cur_frame in reader: # on parcourt les images du film
frames.append(cur_frame)
frames = np.array(frames) # conversion en tableau numpy en sortie de boucle
frames = frames[:,:,:,0] # On ne garde que le "rouge" indice 0 pour avoir un film N&B
np.save(name, frames) # Ecriture sur le disque du tableau dans le fichier name.npy
Note: Il serait aussi possible de travailler directement sur les 'frames' extraits du film sans passer par une sauvegarde dans un fichier npy sur le disque dur. Il y a de nombreuses autres possibilités d'import avec imageio d'images ou de films. Pour en savoir plus et voir des exemples de scripts, vous pouvez lire la documentation en anglais de ce module